
Основы высшей математики для инженеров 2009
.pdf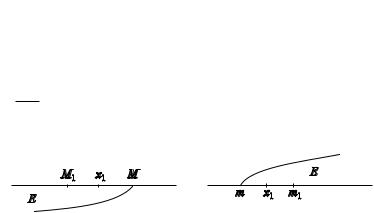
2.2. Числовые последовательности |
71 |
2.2.4. Верхние и нижние грани множеств
Если произвольное множество действительных чисел Е конечно,
то среди его элементов есть наибольший (max E) и наименьший
x E
(min E). Однако это не всегда так, если Е — бесконечное множество.
x E
Например,
E (a, b),
N {1, 2, 3, }.
Возникает вопрос о введении в Е чисел, которые заменяли бы по возможности max E и min E. Такими числами (конечными или беско нечными) являются точная верхняя грань
sup E sup x M
x E
и точная нижняя грань
inf E inf x m.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x E |
|
|
|
|
|
|
ОПРЕДЕЛЕНИЕ. M sup E (m inf E), если: |
|
|
|
|
||||||||||||||||||
1) |
x M (m x) x E; |
|
|
|
|
|
|
|
|
|||||||||||||
2) |
для |
любого |
|
конечного |
1 |
M |
(m1 m) |
|
x1 E: |
M1 x1 M |
||||||||||||
(m1 x1 m). |
|
|
|
|
|
|
|
M62 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
# |
|
n # |
|
1 |
|
|
|||
П р и м е р. E |
|
|
, |
|
, |
|
|
, $ |
|
$; |
min E |
|
|
, но нет max, так |
||||||||
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
2 3 4 |
|
% n 1% |
|
|
|
||||||||||
как |
1 |
|
2 |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Но все же |
это множество |
ограничено |
сверху |
числом |
1, sup E 1, |
|||||||||||||||||
всамом деле:
1)n 1 n; n 1
2) M 1 n : M |
n1 |
|
1. |
|||
|
||||||
1 |
1 |
1 |
n1 |
1 |
|
|
|
|
|
|
|||
Рис. 2.1
Всякое множество F имеет точные верхнюю и нижнюю границы. Ес2 ли Е ограничено сверху, то sup E ; если не ограничено, то sup E . Аналогично, если Е ограничено снизу, то inf E ; если не ограничено
снизу, то inf E .

72 Глава 2. Дифференциальное исчисление функций одной переменной
2.2.5. Теорема Больцано – Вейерштрасса
Пусть задана произвольная числовая последовательность {xn}. Выбе рем из нее бесконечное множество элементов с номерами n1 n2 . Тогда получим новую последовательность{xnk }, которая называется под последовательностью {xn}. Если {xn} сходится к конечному числу или к /, то, очевидно, любая подпоследовательность также сходится к тому же числу.
Последовательность {xn} {1, 1, 1, } не сходится. Однако ее под последовательность {1, 1, 1, …} сходится к 1.
Теорема. Из всякой ограниченной последовательности {xn} можно вы2 делить подпоследовательность {xnk }, сходящуюся к некоторому числу.
2.3. Функции. Предел функции
му закону поставлено в M62 на множестве Е задана однозначная функция
Функция: определение, способы задания. Предел функции. Основные
теоремы о пределах.
1. Пусть Е — множество чисел и пусть каждому x E по некоторо соответствие одно число y, тогда говорят, что
y f (x).
Множество Е называется областью задания или определения f (x). x — независимая переменная, y — зависимая.
Множество E1 всех значений y f (x), где x E, называется обра зом множества Е, или областью значений.
Если
f |
F |
, |
E E1 E2 |
||
то z F(f (x)) называют сложной |
функцией (суперпозицией f и F), |
|
z определена на множестве Е. |
|
|
Функция может быть задана графически, аналитически или табли цей. Функция y f (x) называется четной, если f ( x) f (x). Ее график симметричен относительно оси OY. Функция y f (x) нечетна, если f ( x) f (x). Ее график симметричен относительно биссектрисы 1 го и 3 го координатных углов.
Функция f (x) называется периодической (с периодом T 0), если f (x T) f (x) x.
2.3. Функции. Предел функции |
73 |
2. Важнейшим средством изучения функции является понятие предела, являющееся основным понятием математического анализа.
ОПРЕДЕЛЕНИЕ 1. Число А называется пределом функции f (x) в точке a, если она определена в некоторой окрестности a, за исклю чением, может быть, самой точки a, и если для всякого, сколь угодно малого положительного числа 1 0 можно окружить точку а интерва
лом |
x a |
2, во всех |
точках |
которого выполняется неравенство |
|
f (x) |
A |
|
1. |
|
|
Символически это записывается так: |
|||||
|
|
|
lim |
f (x) A |
(f (x) A). |
|
|
|
x a |
|
|
Смысл этого определения в следующем: если x приближается к a по любому закону, оставаясь не равным a, то соответствующее значение f (x) становится сколь угодно близким к А.
 M62
M62
Рис. 2.2
П р и м е р 1. y f (x) |
x2 4 |
, |
x 2. |
|
|
||||
|
|
|
|
||||||
|
|
x 2 |
|
|
|
|
|
||
lim |
x2 4 |
lim (x 2) 4, |
|
|
|||||
|
|
|
|||||||
x 2 |
|
x 2 x 2 |
|
|
|||||
так как для нас неважно, определена ли функция при x 2. |
|||||||||
П р и м е р 2. Предел |
функции |
y sin |
1 |
при |
|
|
|||
|
|
|
|||||||
|
|
|
|
|
|
x |
|
|
|
x 0 не существует, так как f (x) бесконечное чис |
|
|
|||||||
ло раз меняет знак при x 0 и бесконечное число |
|
|
|||||||
|
|
||||||||
раз принимает значения /1 (рис. 2.3). |
|
|
|||||||
ОПРЕДЕЛЕНИЕ 2. Число А называется преде |
|
Рис. 2.3 |
|||||||
|
|||||||||
лом функции f (x) при x , т. е. A lim f (x), если 1 0 M 0:
x
| f (x) A | 1 x: | x | M.

74 Глава 2. Дифференциальное исчисление функций одной переменной
3. Изучим теперь свойства функций, имеющих предел.
Теорема 1. Если lim f (x) A, где А — конечное число, то в некото2
x a
рой окрестности точки a функция f (x) ограничена, т. е. существует чис2 ло M 0 такое, что | f (x)| M x u(a), x a.
|
Доказательство. |
Пусть |
1 1 2, |
x: |
| x a | 2, | f (x)| | A | |
||
| f (x) A | 1. Следовательно, | f (x)| 1 | A | M. |
|
||||||
|
Теорема 2. Пусть заданы функции u(x), z(x), v(x), причем u z v; |
||||||
lim u lim v A. Тогда lim z A. |
|
|
|||||
x a |
x a |
|
x a |
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
u z v u A z A v A. |
||||
|
1 0 |
21: |u A | 1, |
| x a | 21 1 u A 1; |
||||
|
|
|
M62 |
|
|||
|
1 0 |
22: | v A |
| 1, |
| x a | 1 v A 1. |
|||
|
2 min (21, |
22) | x a | |
: 1 z A 1 lim z A. |
||||
|
|
|
|
|
|
|
x a |
|
Теорема 3. Пусть при x a |
y 0 и |
lim y A. Тогда A 0. |
||||
|
|
|
|
|
|
x a |
|
|
Доказательство. Пусть |
A 0. |
При |
любом |
1 0 A 1 y A 1 |
||
при 2 x a 2. При достаточно малом 1 A 1 0, следовательно, y 0. Получили противоречие.
Теорема 4. Пусть |
lim u(x) A, |
lim v(x) B и u v. Тогда A B. |
||
|
|
x a |
x a |
|
Доказательство. Предположим противное: A B. Далее, |
||||
|
1 0 21: A 1 u(x) A 1, |
|||
|
|
22: B 1 v(x) B 1. |
||
Пусть 2 min (21, 22). Для достаточно малого 1 A 1 B 1 |
||||
|
A B |
|
||
0 1 |
|
v(x) B 1 A 1 u(x) v(x) u(x). |
||
2 |
||||
|
|
|
||
Получили противоречие.

2.4. Непреорывность функции |
75 |
2.4. Непрерывность функции
Определения непрерывности функции. Первый замечательный предел. Второй замечательный предел.
2.4.1. Определения непрерывности функции
Рассмотрим функцию y f (x), рис 2.4. Пусть -x — приращение независимой переменной. Тогда
-f -y f (x0 -x) f (x0)
— приращение функции в точке x0, соответствующее приращению аргумента -x.
Пусть -x 0, тогда для рассматриваемой функции -y 0. Рассмотрим функцию y F(x), рис. 2.5. Здесь F(x0) AB. Пусть
-x 0, но
 -F M62F(x0 -x) F(x0) / 0.
-F M62F(x0 -x) F(x0) / 0.
Рис. 2.4 |
Рис. 2.5 |
ОПРЕДЕЛЕНИЕ 1. Функция y f (x), заданная на [a, b], называ ется непрерывной в точке x0 [a, b], если приращение ее в этой точке, соответствующее -x, стремится к нулю при любом способе стремле ния к нулю -x, т. е.
lim -y 0. |
(1) |
-x 0
Если для функции f (x) не выполнено условие (1), то она называется разрывной в точке x.
Функция, непрерывная в любой точке отрезка (интервала), назы вается непрерывной на этом отрезке (интервале).
Положим x x0 -x. Тогда получим следующее эквивалентное оп ределение непрерывности функции f (x) в точке x0.

76 Глава 2. Дифференциальное исчисление функций одной переменной
ОПРЕДЕЛЕНИЕ 2. Функция y f (x) непрерывна в точке x0, если она определена в некоторой окрестности этой точки и в точке x0 и
lim f (x) f (x0), |
(2) |
x x0
т. е. 1 0 2 0: | f (x) f (x0)| 1 x : | x x0| 2. Равенство (2) можно записать также в виде
lim f (x) f ( lim x).
x x0 x x0
Оно показывает, что под знаком непрерывной функции можно пере ходить к пределу.
П р и м е р ы. 1. Постоянная y C, очевидно, есть функция, непре рывная в каждой точке x. В самом деле, -y 0 для -x, т. е.
lim -y 0.
-x 0
2.y x — непрерывнаMx, так6как2-y -x и -y 0 при -x 0.
3.y sin x. Докажем ее непрерывность, пользуясь определением 2. x x0 cos x x00
|
|
|
|
2 |
|
|
|
2 |
|
|
| sin x sin x | 23sin |
x x033cos |
x x03 |
23sin |
x x03; |
||||||
|
|
|||||||||
0 |
3 |
2 |
33 |
2 |
3 |
3 |
2 |
3 |
||
|
||||||||||
| sin )| |)| ) | sin x sin x0| | x x0| 1,
если | x x0| 1.
Аналогично рассматривая каждую основную элементарную функцию, можно доказать, что она непрерывна в каждой точке, в которой она определена. Т. е. простейшие элементарные
 функции y C, y xn, y loga x, y ax, sin x, cos x, tg x, arcsin x, arccos x, arctg x непрерывны.
функции y C, y xn, y loga x, y ax, sin x, cos x, tg x, arcsin x, arccos x, arctg x непрерывны.
Рис. 2.6
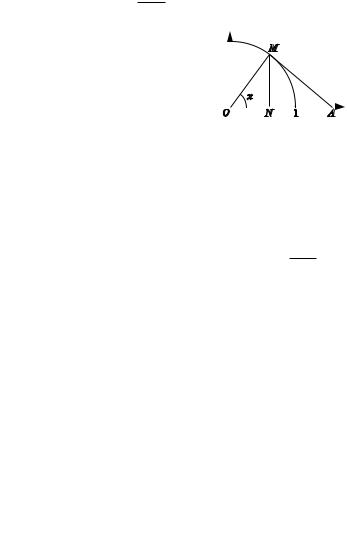
2.4. Непреорывность функции |
77 |
2.4.2. Первый замечательный предел
Теорема.
lim sin x 1.
|
|
|
|
|
|
|
|
|
x 0 x |
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Функция |
y sin x |
не |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
прерывна sin x sin 0 0, при x 0, сле |
|
|
|
|
|
|
|||||||||||||||
|
|
sin x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
довательно, |
|
|
|
|
|
|
, при x 0. Раскроем |
|
|
|
|
|
|
||||||||
|
x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
эту неопределенность. Из рис. 2.7 следует, |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
что при 0 x |
' |
|
0 sin x x tg x, так как |
|
|
|
Рис. 2.7 |
|
|||||||||||||
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
MN sin x, |
|
AM tg x, OM 1 (AM |
OM), а |
угол х равен длине |
дуги |
||||||||||||||||
окружности единичного радиуса OM. |
|
|
|
|
|
|
|
|
|||||||||||||
Тогда при условии sin x 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
x |
|
|
tg x |
, или 1 |
|
x |
|
|
1 |
|
1 |
sin x |
cos x. |
(3) |
|||||
sin x |
|
|
sin x |
cos x |
|
||||||||||||||||
|
|
sin x |
|
|
|
|
|
x |
|
||||||||||||
Неравенства (3) верны и для ' x 0, так как cos x и sin x четные
|
2 |
|
x |
функции. Далее, cos x — |
M62непрерывная функция, следовательно, |
||
|
lim cos x cos0 1. |
||
|
x 0 |
|
|
Тогда по теореме о переходе к пределу в неравенствах |
|||
|
lim |
sin x |
1. |
|
|
||
|
x 0 |
x |
|
Теорема доказана.
2.4.3. Второй замечательный предел
Теорема.
|
|
1 x |
||
lim 1 |
|
|
|
e. |
|
||||
x |
|
x |
|
|
Доказательство. Было установлено, что
|
|
1 n |
||
lim 1 |
|
|
|
e, |
|
||||
n |
|
n |
|
|

78 Глава 2. Дифференциальное исчисление функций одной переменной
где n — целые числа. Пусть x , принимая как целые, так и дроб ные значения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n x n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
и 1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
x |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
x |
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 n 1 |
|
|
1 |
x |
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пусть x , тогда n , при этом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
1 n 1 |
|
|
|
|
|
|
|
1 |
n |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||
lim 1 |
|
|
|
|
lim |
1 |
|
|
|
1 |
|
|
lim |
1 |
|
|
|
|
lim |
|
1 |
|
|
|
|
e 1 e; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
n |
n |
|
|
|
n |
|
|
|
|
|
n |
|
|
n |
|
n |
|
|
|
|
|
n |
|
|
n |
|
|
|
|
n |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n 1 |
|
|
|
|
|
|
|
|
|
|
|
1 n 1 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
lim |
1 |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
lim 1 |
|
|
|
|
|
|
|
lim |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
e. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
||||||||||||||||||||||
n |
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
и |
|
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M62, то при x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, |
lim |
1 |
|
|
|
|
|
e. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
З а м е ч а н и е. Если положить |
1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim (1 ))) e.
) 0
2.5. Бесконечно малые и бесконечно большие функции
Бесконечно малые функции и их свойства. Теоремы о пределах функ ций. Бесконечно большие функции, их связь с бесконечно малыми.
2.5.1. Бесконечно малые функции и их свойства
ОПРЕДЕЛЕНИЕ 1. Функция ) )(x) называется бесконечно ма
лой при x a или x , если |
|
lim )(x) 0 или |
lim )(x) 0, |
x a |
x |
т. е. 1 0 2 0: |)(x)| 1 | x a | 2.

|
2.5. Бесконечно малые и бесконечно большие функции |
79 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.8 Рис. 2.9
Теорема 1. Алгебраическая сумма двух, трех и вообще конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство. Докажем теорему для случая двух слагаемых.
Пусть u(x) )(x) *(x), где |
lim )(x) 0, |
lim *(x) 0. |
||||||
|
|
x a |
x a |
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
1 0 |
2 : |
x : | x a | 2 |
|)(x)| |
1 |
, |
|||
|
|
|||||||
|
1 |
|
1 |
2 |
|
|||
|
|
|
|
|
||||
|
2 : |
x : | x a | 2 |
|*(x)| |
1 |
. |
|||
Пусть 2 min (21, 22). Имеем:M62 2
|u | |)(x) *(x)| |)(x)| |*(x)| 1 x : | x a | 2.
Теорема 2. Произведение бесконечно малой функции ) )(x) на огра2 ниченную функцию z(x) при x a есть бесконечно малая функция.
Доказательство. Для M 0 окрестность точки a такая, что
| z| M x : | x a | 21.
Далее, |
|
|
|
1 0 22: | x a | 22 |
|)(x)| |
1 |
. |
|
|||
|
|
M |
|
1 M 1 x : | x a | 2.
M
Следствие 1. Если lim )(x) 0, lim *(x) 0, то lim )(x) *(x) 0, так как *(x) — величина ограниченная. Это справедливо для любого ко нечного числа сомножителей.
Теорема 3. Частное )(x) от деления бесконечно малой функции )(x) z(x)
на z(x), предел которой отличен от нуля, есть величина бесконечно малая.

80 Глава 2. Дифференциальное исчисление функций одной переменной
Доказательство. Пусть lim )(x) 0. |
Покажем, |
что |
функция |
1 |
|||||||||||||
z(x) |
|||||||||||||||||
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|||
ограничена. Пусть |
lim z(x) b. Возьмем 0 1 |b|, тогда 2: | z(x) b| |
||||||||||||||||
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|b z(x)| 1, т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
||||
|b| | z(x)| 1 | z(x)| |b| 1 0 |
|
|
|
|
M. |
|
|||||||||||
z(x) |
| z(x)| |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|b| 1 |
|
||||||||
Тогда )(x) |
1 |
— бесконечно малая функция. |
|
|
|
|
|
|
|||||||||
z(x) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема 4. |
Если |
f (x) A )(x), то |
lim f (x) A. |
Обратно, если |
|||||||||||||
|
|
|
|
|
x a |
|
|
|
|
|
|
||||||
lim f (x) A, то |
f (x) A )(x), где )(x) — бесконечно малая функция. |
|
x a |
|
|
Доказательство. Пусть |
f (x) A )(x) | f (x) A | |)(x)|, но |
|
1 0 2: | x a | 2 |
|)(x)| 1 | f (x) A | 1 lim f (x) A. |
|
нечно малая и |
fx(x)a A )M62(x). |
|
|
|
x a |
Обратно, пусть |
lim f (x) A | f (x) A | 1 f (x) A )(x) — беско |
|
2.5.2. Теоремы о пределах функций
Теорема 1. Предел алгебраической суммы конечного числа слагаемых
равен сумме их пределов: |
|
|
|
|
|
|
|||
lim (f (x) f |
(x) f (x)) lim |
f (x) lim f |
(x) lim f (x). |
||||||
x a 1 |
2 |
|
|
n |
x a |
1 |
x a 2 |
x a n |
|
Доказательство. Докажем теорему для случая двух слагаемых. |
|||||||||
Пусть lim |
f (x) |
A , lim f (x) A . Тогда |
|
|
|||||
x a |
1 |
1 |
x a |
2 |
2 |
|
|
|
|
|
|
f1(x) A1 )1(x), f2(x) A2 )2(x) |
|
||||||
|
|
f1(x) f2(x) (A1 A2) ()1(x) )2(x)). |
|
||||||
Функция )1(x) )2(x) — бесконечно малая, следовательно, |
|||||||||
|
lim (f (x) f |
(x)) A |
A |
lim f (x) lim f (x). |
|||||
|
x a 1 |
2 |
1 |
2 |
|
x a 1 |
x a |
2 |
|
