
Основы высшей математики для инженеров 2009
.pdf

192 Глава 3. Интегральное исчисление функций одной переменной
Теорема 4. Если f (x) 0 и lim { f (x)xm} A , A 0, т. е. f (x) ~ |
A |
|||||||
xm |
||||||||
|
|
x |
|
|
|
|||
при x , то: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
1) |
при m 1 |
интеграл D f (x)dx сходится; |
||||||
2) |
при m 1 |
a |
|
|
|
|
||
интеграл расходится. |
||||||||
П р и м е р. Исследовать на сходимость интеграл |
||||||||
|
|
|
dx |
|
|
|
||
|
|
D |
|
|
. |
|||
|
|
|
|
|
||||
|
|
3 |
||||||
|
|
1 |
|
x 1 |
||||
3.12.3. Интегралы от неограниченных функций (интегралы второго рода)
Пусть функция y f (x) определена на отрезке [a, b], а при x b не ограничена. Тогда точка b называется особой точкой, а интеграл от функции, неограниченной при x b, определяется следующим об разом:
b |
f (x)dx lim |
b 1 |
|
|
|
f (x)dx. |
|
|
M62 |
||
D |
10 |
D |
|
a |
|
a |
|
Если предел существует, то интеграл называется сходящимся. Аналогично определяется интеграл от функции, разрывной на ле
вом конце промежутка:
bb
D f (x)dx lim |
D f (x)dx. |
10 |
а 1 |
a |
Если f (x) терпит разрыв в точке c (a c b), то
b |
c |
b |
D f (x)dx D f (x)dx D f (x)dx,
a |
a |
c |
если оба интеграла справа существуют.
П р и м е р. Исследовать на сходимость интеграл
b
dx
Da (b x)) .
194 |
Глава 3. Интегральное исчисление функций одной переменной |
3.13. Приближенные методы вычисления определенных интегралов
Постановка задачи. Формула прямоугольников. Формула трапеций. Формула парабол (формула Симпсона). Приближенное вычисление интегралов с использованием формулы Тейлора.
3.13.1. Постановка задачи
b
Пусть требуется вычислить D f (x)dx, где f (x) — непрерывная функ
a
ция. Если может быть найдена первообразная от f (x), то можно вос пользоваться формулой Ньютона – Лейбница. Если же первообразная не может быть найдена (интеграл не берущийся), или функция f (x) за дана графически или таблично, то прибегают к приближенным фор мулам, точность которых может быть сделана сколь угодно большой.
Приближенные методы основаны на геометрическом истолкова
b
нии D f (x)dx как площади соответствующей криволинейной трапеции.
Сутьaприближенного вычисленияM62интеграла заключается в том, что кривая y f (x) заменяется новой, достаточно «близкой» к ней кривой, для которой площадь криволинейной трапеции легко вычисляется. Тогда искомая площадь (т. е. искомый интеграл) приближенно равна площади криволинейной трапеции, ограниченной новой кривой.
В зависимости от выбора новой кривой получаются различные приближенные формулы интегрирования.
3.13.2. Формула прямоугольников |
|
|
|||
|
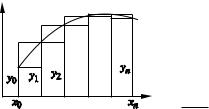
Итак, пусть на [a, b] задана непрерывная |
||||
функция f (x). Для простоты будем считать, |
|||||
что |
f (x) 0 на |
[a, |
b]. Нужно |
вычислить |
|
b |
|
|
|
|
|
D f (x)dx. Разделим отрезок [a, b] на n равных |
|||||
a |
|
|
|
|
|
частей точками |
x0, |
x1, …, |
xn. |
Положим |
|
h b a . Обозначим через y , |
y , …, y зна |
||||
Рис. 3.21 |
n |
|
0 |
1 |
n |
|
|
|
|
||
чения функции f (x) в точках x0, x1, …, xn: |
|||||
y0 f (x0), |
y1 f (x1), , |
yn f (xn). |
|
|
|
3.13. Приближенные методы вычисления определенных интегралов |
195 |
||||||||
Составим суммы |
y0h y1h yn 1h, |
|
(1) |
||||||
|
|
|
|||||||
|
|
y1h y2 h ynh. |
|
(2) |
|||||
Первая из этих сумм выражает площадь ступенчатой фигуры, состоя |
|||||||||
щей из «входящих» прямоугольников, а вторая — из «выходящих». |
|||||||||
Обе суммы, (1) и (2), являются интегральными для функции |
f (x) на |
||||||||
[a, b], поэтому имеют место приближенные равенства |
|
||||||||
|
b |
|
|
|
|
|
|
|
|
|
D f (x)dx = h(y0 y1 yn 1), |
|
|
||||||
|
a |
|
|
|
|
|
|
|
(3) |
|
b |
|
|
|
|
|
|
|
|
|
D f (x)dx = h(y1 y2 yn). |
|
|
||||||
|
a |
|
|
|
|
|
|
|
|
Формулы (3) — формулы прямоугольников. |
|
|
|||||||
Эти формулы остаются справедливыми и для знакопеременной на |
|||||||||
[a, b] функции f (x). |
|
|
|
|
|
|
|
|
|
Чем больше n, тем больше точность формул (3). |
|
||||||||
|
3.13.3. Формула трапеций |
|
|
||||||
|
|
M62 |
|
|
|||||
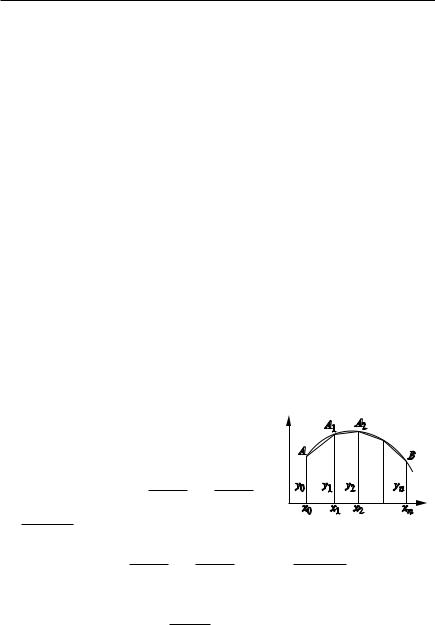
Естественно предположить, что более точное значение определен |
|||||||||
ного интеграла будет получено в том случае, когда кривая y f (x) за |
|||||||||
меняется не ступенчатой линией, а вписанной ломаной. Тогда пло |
|||||||||
щадь криволинейной |
трапеции |
|
заменится |
|
|
||||
суммой площадей прямолинейных трапе |
|
|
|||||||
ций, ограниченных сверху |
хордами |
A0 A1, |
|
|
|||||
A1A2, …, An 1B. Площади этих трапеций |
|
|
|||||||
равны соответственно |
y0 y1 h, |
y1 y2 h, |
|
|
|||||
|
|
2 |
|
|
|
2 |
|
|
|
…, yn 1 yn h, поэтому |
|
|
|
|
|
Рис. 3.22 |
|
||
2 |
|
|
|
|
|
|
|
|
|
b |
|
y1 h y1 |
y2 h yn 1 yn h, |
|
|||||
D f (x)dx = y0 |
|
||||||||
a |
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
b |
|
y |
0 |
y |
n y |
|
|
|
|
|
f (x)dx |
y y |
(4) |
||||||
D |
= h |
2 |
. |
||||||
|
|
|
|
1 |
2 |
n 1 |
|
||
a |
|
|
|
|
|
|
|
|
|

3.13. Приближенные методы вычисления определенных интегралов |
197 |
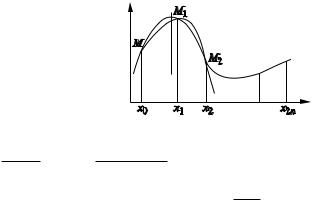
Тогда
x2 |
|
h |
|
|
D |
y(x)dx |
(y0 4y1 y2). |
||
|
||||
x0 |
3 |
|
||
|
|
|
||
Аналогичным образом получаются выражения для всех следующих частичных отрезков интегрирования, объединенных попарно:
x4 |
h |
|
|
|
D f (x)dx = |
(y2 |
4y3 y4), |
||
|
||||
3 |
||||
x2 |
|
|
|
. . . . . . . . . . . . . . . . . . .
x2n |
h |
|
|
|
D f (x)dx = |
(y2n 2 |
4y2n 1 y2n). |
||
|
||||
3 |
||||
x2n 2 |
|
|
|
Складывая данные соотношения, получим
bD f (x)dx = h (y0 4y1M62y2 4y3 y2n 2 4y2n 1 y2n), 3
a
или
b |
h |
|
|
|
|
D f (x)dx = |
[y0 |
y2n 2(y2 |
y4 y2n 2) 4(y1 y3 y2n 1)], (6) |
||
|
|||||
3 |
|||||
a |
|
|
|
|
где h b a .
2n
(6)— формула Симпсона.
При вычислении интеграла по методу Симпсона поступают сле дующим образом:
1)вычисляют J2n и J4n;
2)сравнивают результаты вычислений и оставляют первые совпа дающие знаки.
За м е ч а н и е. При одном и том же числе точек деления отрезка фор мула Симпсона дает более точный результат, чем формула прямоугольни ков и трапеций.

ГЛАВА 4
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
4.1. Основные понятия и определения. Функции двух переменных и области их определения. График функции двух переменных.
Предел и непрерывность
До сих пор мы изучали совместное изменение двух переменных, из которых одна зависела от другой: значением независимой переменной уже вполне определялось значение зависимой переменной или функ ции. В инженерной практике нередки, однако, случаи, когда незави симых переменных оказывается несколько, и для определения значе ния функции необходимо предварительно установить значения, со вместно принимаемые всемиM62этими независимыми переменными.
1. Так, например, по закону Ома, напряжение U в цепи электри ческого тока связано с сопротивлением R цепи и с силой тока I зави симостью U RI . Если U и R считать данными, то отсюда определит ся I как функция от U и R:
I U . R
2. Пусть температура массы газа, находящегося под поршнем ци линдра, не постоянна: тогда объем V и давление P одного моля газа связаны с ее температурой Т, так называемой, формулой Клапейрона
PV RT (R const).
Отсюда, считая, например, V и Т независимыми переменными, функ цию P можно выразить через них так:
P RT .
V
3. Изучая физическое состояние какого нибудь тела, часто прихо дится наблюдать изменение его свойств от точки к точке. Таковы плот ность, температура, электрический потенциал и т. п. Все эти величины суть «функции точки» или, если угодно, функции от координат x, y, z точки. Если физическое состояние тела меняется во времени, то к этим
4.1. Основные понятия и определения… |
199 |
независимым переменным присоединяется еще и время, t. В этом слу чае мы имеем дело с функциями от четырех независимых переменных.
Уточнение понятия функции в случае нескольких независимых пе ременных начнем с простейшего случая, когда этих переменных две.
4.1.1. Функции двух переменных и области их определения
ОПРЕДЕЛЕНИЕ. Функцией двух переменных называется прави ло, по которому каждой паре чисел (x, y) M соответствует число z L при условии, что любое число z L соответствует хотя бы одной паре (x, y) M.
x и y — независимые переменные, М — область определения функции, L — множество значений функции, z — зависимая перемен ная. Функциональная зависимость между z и x, y обозначается, анало гично случаю одной независимой переменной, так:
z f (x, y).
M62
Способы задания функции двух перемен ных — табличный и аналитический. При ана литическом способе задания область определе
ния функции часто не задается и ее приходит ся отыскивать. Например,
z  1 x2 y2 1 x2 y2 0 x2 y2 1.
1 x2 y2 1 x2 y2 0 x2 y2 1.
Рис. 4.1
z arcsin(x2 y2 2);
1 x2 y2 2 1 1 x2 y2 3.
Так как каждой паре чисел x, y соответствует единственная точка плоскости P(x, y), то
функцию двух переменных можно рассматри
вать как функцию точки и писать z f (P).
Рис. 4.2
4.1.2. График функции двух переменных
Графиком функции двух переменных является в общем случае по верхность. Действительно, пусть G — область определения функции. Каждой точке P(x, y) из этой области соответствует единственная
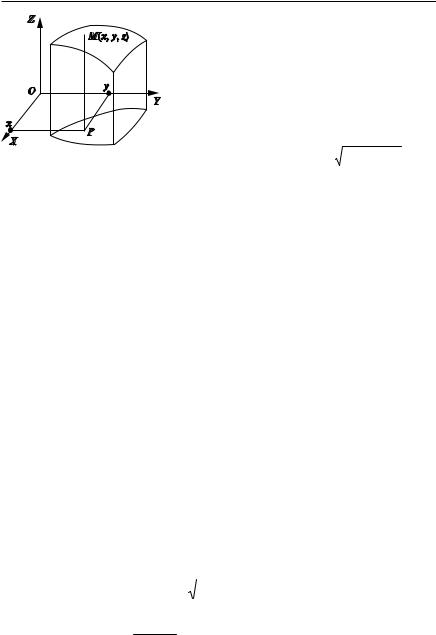
200 Глава 4. Дифференциальное исчисление функций многих переменных
точка M(x, y, z) некоторой поверхности, где z f (P) f (x, y). Проекция этой точки на плоскость XOY совпадает с Р.
Если поверхность является графиком функции двух переменных, то уравнение z f (x, y), определяющее эту поверхность, называется уравнением поверхности. Так, верхняя часть сферы x2 y2 z2 1 являет
Рис. 4.3 |
ся графиком функции |
z 1 x2 y2 . |
|
|
4.1.3. Предел и непрерывность
Введем понятие окрестности точки. Для функции одной перемен ной под окрестностью точки понимается интервал, содержащий эту точку. При введении понятия предела для функции z f (x, y) окрест
ность точки определяется на плоскости XOY.
Окрестностью точки P0(x0, y0) называется множество всех внут ренних точек круга с центром в этой точке. 2 окрестностью будем на
M62
зывать круг радиуса 2 за исключением точек его границы.
Число А называется пределом функции двух переменных z f (x, y) f (P) при P P0, если 1 0 найдется такая 2 окрестность точки P0, что для любой точки P(x, y) из этой окрестности (за исклю чением, может быть, самой точки P0) имеет место неравенство
|
|
|
|
| f (P) A | 1 |
|
или |
| f (x, |
y) A | 1, |
|||||||||
как только |
|
P0P |
|
2 или |
|
x x0 |
|
2, |
|
y y0 |
|
2. |
|||||
|
|
|
|
|
|
||||||||||||
При этом пишут |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
lim f (P) A |
|
или |
lim |
f (x, y) A. |
|||||||||
|
|
|
|
P P0 |
|
|
|
x x0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
y y0 |
|
|
|||
П р и м е р 1. Найти |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
lim |
|
|
|
x2 |
y2 |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x 0 |
2 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
y 0 |
|
x y 1 1 |
|||||||||
Здесь P(x, y) P(0, 0), т. е. + 0 (+ — расстояние от P(x, y) до начала координат). Но + 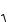
 x2 y2 .
x2 y2 .

