
Основы высшей математики для инженеров 2009
.pdf
2.15. Асимптоты. План исследования функций и построения графиков 121
Аналогичные формулы имеют место и для x . Отметим, что при x и x k и b могут быть разными. Соответственно раз личают левую и правую наклонные асимптоты. Если хотя бы один из
пределов lim |
f (x) |
|
|
или |
|
lim (f (x) kx) не существует, то кривая асим |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
x x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
птоты не имеет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
П р и м е р ы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
y |
x2 x 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x 1 |
|
|
|
|
|
|
|||||||||||
|
|
|
k |
|
lim |
|
f (x) |
|
lim |
|
|
1 |
; |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
x |
x |
|
|
x (2 x 1)x |
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
lim |
|
f (x) |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x 2 |
1 |
|
|||||||||
|
|
|
b1 b2 |
lim f (x) |
|
x |
|
|
lim |
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
2(2 x 1) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
4 |
|
|||||||||||||||
|
|
|
y |
1 |
x |
1 |
|
M62— левая и правая асимптота. |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
y xe x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
k lim |
xe x |
0, |
|
b lim |
|
x |
0 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
x |
x |
|
|
|
|
|
1 |
|
x ex |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y 0 — горизонтальная асимптота.
2.15.2. Общая схема исследования функции и построения ее графика
1.Нахождение области определения функции, интервалов непре рывности и точек разрыва.
2.Нахождение асимптот графика функции.
3.Нахождение интервалов монотонности и экстремумов.
4.Нахождение интервалов выпуклости, вогнутости и точек пе региба.
5.Исследование функции на четность, периодичность.
6.Точки пересечения с осями координат.
7.Построение графика.
122Глава 2. Дифференциальное исчисление функций одной переменной
2.15.3.Дифференциал длины дуги
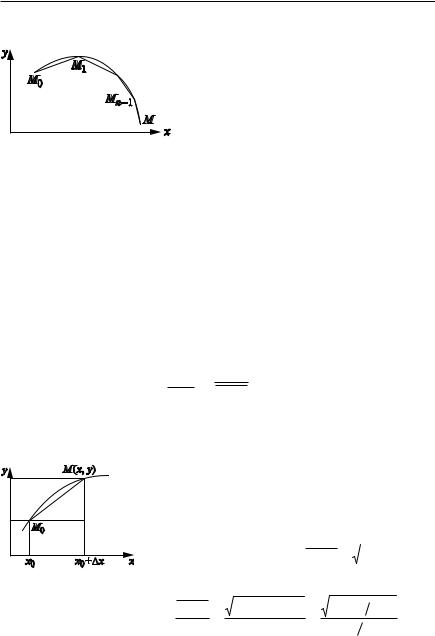
Рис. 2.31 |
Пусть дуга кривой M0M есть график функции y f (x), определенной на (a, b). Определим длину дуги кривой. Для этого разобьем кривую точками M0, M1, M2 , …, Mn 1, M на n частей. Соединив точки ме жду собой, получим ломаную линию, вписанную в дугу M0M. Обозначим ее длину через Pn.
ОПРЕДЕЛЕНИЕ. Длиной S кривой M0M называется предел, к ко торому стремится длина ломаной Pn при неограниченном увеличении числа ее звеньев и при стремлении наибольшего звена к нулю, если такой предел существует и не зависит от способа выбора вершин ло маной M0, M1, …, Mn 1, M.
Можно доказать следующие утверждения.
1.Если на [a, b] f (x) и f (x) непрерывны, то дуга кривой y f (x), за2 ключенная между точкамиM62[a, f (a)] и [b, f (b)], имеет вполне определен2 ную длину.
2.При перечисленных условиях на f (x) отношение длины любой дуги кривой к длине стягивающей ее хорды стремится к 1 при стремлении
длины хорды к 0:
lim M0M 1.
M 0M 0 M0M
На основе этих двух теорем можно вывести формулу для дифферен циала длины дуги кривой.
Пусть кривая на плоскости задана уравне нием y f (x), где f (x) — дифференцируемая функция, M0(x0, y0) — фиксированная точка
на кривой. |
|
|
|
Обозначим через S длину дуги M0M. Тогда |
|||
S S (x). Найдем S (x). |
Пусть x0 получило |
||
приращение |
-x. Имеем: M0M (-x)2 (-y)2 ; |
||
|
|
|
|
-S — длина дуги M0M, |
|
|
|
Рис. 2.32 |
|
|
|
M0M |
(-x)2 (-y)2 |
1 4-y -x52 |
. (*) |
-S |
-S |
-S -x |
|

2.15. Асимптоты. План исследования функций и построения графиков 123
Перейдем к пределу в обеих частях равенства (*) при -x 0 и вос
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0M |
|
|
|
|||||||||||
пользуемся тем, что |
|
lim M0M 0 и |
lim |
|
1, |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
-x 0 |
|
|
|
|
|
|
|
|
|
-x 0 -S |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
lim |
-y |
|
dy |
; |
|
|
lim |
|
|
-S |
|
|
|
dS |
. |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
-x 0 -x dx |
|
|
-x 0 -x |
|
|
dx |
|
|
|
||||||||||||||||||||||||||||||||
В результате получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
lim 1 |
|
|
|
-y 2 |
|
|
|
|
|
|
|
|
dy 2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
-x 0 |
|
|
|
|
|
-x |
|
|
|
|
|
|
|
|
dx |
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
|
|
|
lim |
|
-S |
|
|
|
|
|
|
|
dS |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
-x 0 -x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dS |
|
|
|
|
dy |
2 |
|
|
|
|
|
|
|
|
|
dy 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx dx2 dy2 . |
||||||||||||||||||||||||||
|
|
|
|
1 |
|
; |
dS 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Мы получили выражение для дифференциала длины дуги в случае, когда кривая задана в виде y f (x). Однако эта формула остается справедливой и для случая параметрического задания кривой:
y y(t), |
x x(t): |
dx M62x (t)dt; dy y (t)dt; |
|
dS 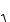
 [x (t)]2 [y (t)]2 dt.
[x (t)]2 [y (t)]2 dt.
Если кривая задана в полярных координатах уравнением + +((), то рассматривая уравнения x + cos (, y + sin ( как параметрические с параметром (, получим
dx d+ cos ( + sin (; d( d(
dy d+ sin ( + cos (; d( d(
dx 2 |
|
dy 2 |
|
d+ 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
+2; |
||
|
|
|
|
|
|||||||||
d( |
|
d( |
|
d( |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
d+ 2 |
|
|
|||
|
dS |
|
|
+2 |
|
|
|
|
d(. |
||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
d( |
|
|
|||

124 Глава 2. Дифференциальное исчисление функций одной переменной
2.16. Кривизна плоской кривой
Кривизна. Вычисление кривизны кривой. Радиус кривизны. Окружность кривизны. Центр кривизны. Эволюта и эвольвента.
2.16.1. Кривизна
Одним из элементов, характеризующих форму кривой, является степень ее искривленности, изогнутости.
Пусть кривая имеет в каждой точке касательную. Проведем в двух точках кривой касательные к ней и обозначим через ) угол поворота касательной при пе реходе от М к M1, угол считаем положительным. Этот
угол называется углом смежности.
Средней кривизной дуги |
|
называется отно |
||
MM1 |
||||
шение угла смежности ) к длине дуги: |
||||
Рис. 2.33 |
) |
|
|
|
Kcp |
. |
|
|
|
|
|
|
||
дл. MM1
Для некоторых кривых средняя кривизна есть величина постоянная,
радиуса |
|
) |
1 . Однако в общем |
||
например, для окружностиM62R Kcp |
|
|
|
|
|
R) |
|
R |
|||
|
|
|
|||
случае средняя кривизна может быть разной для разных участков дуги (чем больше изогнута кривая, тем больше кривизна).
ОПРЕДЕЛЕНИЕ. Кривизной дуги в точке М называется предел
средней кривизны дуги MM1 при условии, что точка M1 неограничен но приближается по кривой к точке М:
K lim Kcp.
M1 M
В частности, кривизна окружности радиуса R в любой точке равна 1 .
R
Легко видеть, что кривизна прямой равна 0.
2.16.2. Вычисление кривизны кривой
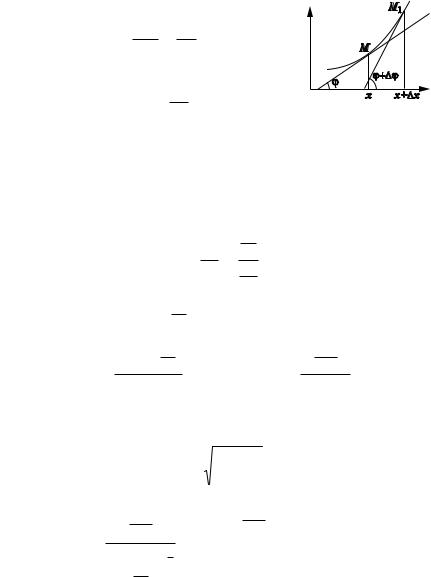
Пусть кривая задана уравнением y f (x), где f (x) — дважды диф ференцируемая функция, M(x, y) — точка на кривой. Вычислим кри визну в этой точке. Проведем касательные к кривой в точках M(x, y)
2.16. Кривизна плоской кривой |
125 |
и M1(x -x, y -y). ( и ( -( — углы наклона этих касательных, -S — длина дуги MM1.
По определению
Kcp | -(| 3-(3, | -S | 3-S3
так как | -(| — угол смежности. Тогда
K lim 3-(3.
-S 03-S3 Рис. 2.34
Здесь следует также отметить, что -( — это угол поворота касательной при перемещении точки касания по дуге кривой на величину -S. По этому можно дать и наглядно очевидное определение кривизны кривой следующим образом: кривизна кривой есть угловая скорость вращения касательной при перемещении точки касания по кривой.
Так как ( и S являются функциями от x, то
3 d(3 M6K 3d(3 3 dx23.
3dS3 3dS3
3 dx3
Заметим теперь, что tg ( dy ( arctg dy ; dx dx
|
|
|
|
|
|
|
|
|
dy |
|
|
|
d( |
|
d arctg |
|
|||
|
|
|
|
|
|
dx |
|||
|
|
|
dx |
|
dx |
||||
|
|
|
|
|
|
||||
dS |
было вычислено ранее: |
||||||||
|
|||||||||
dx |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
dS |
|
|
|
|
|
|
|
|
|
dx |
Итак, |
|
|
|
|
|||||
|
|
|
|
|
|
|
d2 y |
|
|
|
|
d( |
|
dx2 |
3 , |
||||
|
|
|
|
|
|
|
|||
|
|
dS |
|
|
|
||||
|
|
|
|
|
|
7 |
dy 2 :2 |
||
|
|
|
|
|
|
91 |
|
|
< |
|
|
|
|
|
|
9 |
dx |
< |
|
|
|
|
|
|
|
8 |
|
|
; |
|
1 |
|
dy |
|
|||
|
|
|
|
|
|
|
|
|
dy 2 |
|
|||||
1 |
dx |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dx |
|
|
|
|
||
dy 2  1
1  .
.
dx
d2 y
dx2 .
dy 2
1 
dx
|
|
3d2 y3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
K |
|
3dx23 |
|
|
|
|
|
| y | |
|
|
|
. |
||
|
|
2 |
|
3 |
|
|
|
|
3 |
|
||||
7 |
|
:2 |
|
|
[1 |
2 |
2 |
|
|
|||||
91 |
dy |
|
|
|
|
(y ) |
] |
|
|
|||||
|
|
|
< |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||||
9 |
dx |
< |
|
|
|
|
|
|
|
|
|
|||
8 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|

126Глава 2. Дифференциальное исчисление функций одной переменной
Пр и м е р 1. Найти кривизну параболы y2 2 px в точке с коорди натами (0, 0).
Вычисление кривизны кривой, заданной параметрически. Если линия
задана параметрически: x x(t), |
y y(t), то |
|
|
|
|
|
||||||||||||||
|
|
dy y |
d2 y |
|
|
|
y 2 xt |
x 2 yt |
|
|
|
|
||||||||
|
|
|
|
|
t |
; |
|
|
|
|
|
t |
t |
; |
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|||||||||
|
|
dx |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
t |
dx |
|
|
|
|
(xt) |
|
|
|
|
||||
|
|
|
| yt2 xt xt2 yt| |
|
|
|
|
| yt2 xt xt2 yt| |
||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
||||||||
|
|
|
|
|
|
2 |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(x )3 |
|
|
(xt) |
(yt) |
|
|
|
|
[(xt)2 (yt)2]2 |
|||||||||
|
|
|
|
2 |
|
|||||||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
(xt) |
|
|
|
|
|
|
|
|
|
|
|||
Пр и м е р 2. Найти кривизну кривой y t 3, x t 2 в точке (1, 1).
2.16.3.Радиус кривизны. Окружность кривизны. Центр кривизны
M621 [1 (y )2 |
]2 |
|
ОПРЕДЕЛЕНИЕ. Величина, обратная кривизне |
K, называется ра |
|
диусом кривизны данной линии в рассматриваемой точке: |
||
|
|
3 |
R |
|
. |
K |
| y | |
|
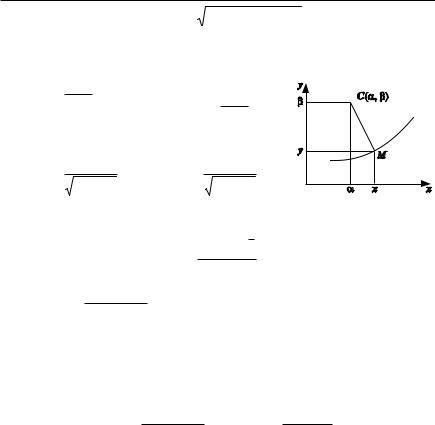
Построим в точке М нормаль к кривой, направ ленную в сторону вогнутости кривой и отложим на ней отрезок МС, равный радиусу кривизны R в точке М. Точка С называется центром кривиз ны, а окружность радиуса R с центром в этой
точке — окружностью кривизны (рис. 2.35). Из определения окружности кривизны вытекает, что в точке М ли
ния и ее окружность кривизны имеют общую касательную.
Пусть линия задана уравнением y f (x). Запишем уравнение нор мали к линии y f (x) в точке (x, f (x)):
Y y 1 (X x).
|
y |
|
|
Точка С лежит на этой линии, поэтому |
|
||
* y |
1 |
() x). |
(1) |
|
|||
|
y |
|
|
|
|
|
|
|
2.16. Кривизна плоской кривой |
127 |
||||
Кроме того, |CM | R, поэтому |
() x)2 (* у)2 R или |
|
||||||||
|
|
|
|
|
|
() x)2 (* у)2 R2. |
(2) |
|||
Решая совместно систему уравнений (1) – (2), получим: |
|
|||||||||
|
|
1 |
|
() x)2 |
|
|
1 : |
|
||
&(* y)2 |
(y )2 |
|
7 |
|
||||||
|
2 |
|
() x)2 |
91 |
2 |
< R2, |
|
|||
& |
2 |
|
|
2 |
|
8 |
(y ) |
; |
|
|
(* y) R () x) |
|
|
|
|
|
|||||
или |
|
|
|
|
|
|
|
|
|
|
) x / |
|
y |
R, |
* y |
1 |
R. |
|
|||
|
|
1 (y )2 |
|
1 (y )2 |
|
|||||
|
|
|
|
|
|
|
|
|
Рис. 2.36 |
|
Подставим вместо R его выражение |
|
|
||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
R (1 (y ) ) . |
|
|||
|
|
|
|
|
|
|
| y | |
|
|
|
Тогда ) x / y (1 |
(y )2) |
M62 |
|
|||||||
; * y |
(1 |
(y ) ). |
|
|||||||
|
|
|
|
| y | |
|
| |
y | |
|
|
|
Чтобы узнать, какие знаки брать в последних формулах, рассмот |
||||||||||
рим два случая. |
|
|
|
|
|
|
||||
1. |
y 0; тогда кривая вогнута, рис. 2.36, * y и поэтому нужно |
|||||||||
брать нижние знаки. При этом | y | y , |
|
|||||||||
|
|
|
|
) x y (1 (y )2) ; |
* y (1 (y )2) . |
(3) |
||||
|
|
|
|
|
|
y |
|
|
y |
|
2. y 0; тогда нужно брать верхние знаки, но | y | y . Поэтому формулы (3) остаются справедливыми и в этом случае.
2.16.4. Эволюта и эвольвента
Если точка М перемещается по данной кривой, то соответствую щий ей центр кривизны также описывает некоторую кривую. Множе ство всех центров кривизны данной кривой называется ее эволютой. Сама линия по отношению к своей эволюте — эвольвента (развертка).
Уравнения (3) можно рассматривать как параметрические уравне ния эволюты. Если из них исключить параметр x, то получим уравне ние эволюты на плоскости {), *}.

128 Глава 2. Дифференциальное исчисление функций одной переменной
П р и м е р. y x2 . Написать уравнение эволюты. 2
Свойства эволюты и эвольвенты.
1. Нормаль к эвольвенте является касательной к эволюте в соот ветствующей точке, рис. 2.37, где точки P1, P2, P3 находятся на эволь венте, а точки М1, М2, М3 на эволюте и являются центрами кривизны эвольвенты в показанных точках P1, P2, P3. В соответствии с данным свойством точки М1, М2, М3 являются точками касания к эволюте ра
диусов кривизны М1P1, М2 P2, М3P3.
2. Если на некотором участке эвольвенты радиус кривизны меня ется монотонно, то приращение радиуса кривизны на этом участке равно по абсолютной величине длине дуги соответствующего участка
эволюты: M1M2 M2 P2 M1P1.
|
При помощи этих свойств можно восстано |
|
вить эвольвенту по эволюте. Представим себе, что |
|
на эволюту навернута гибкая нерастяжимая нить |
|
от конца эволюты М3 через точки М2, М1, до за |
|
данной точки Р1 эвольвенты. Если к концу нити в |
|
точке Р1 прикрепить карандаш и развертывать |
|
вправо в натянутом состоянии, то карандаш |
Рис. 2.37 |
нить M62 |
|
опишет эвольвенту и пройдет через точки Р2, Р3. |
2.17. Комплексные числа
Комплексные числа. Определение, геометрическое изображение. Три гонометрическая форма комплексного числа. Действия над комплекс ными числами. Показательная функция в комплексной области. Форму ла Эйлера. Некоторые сведения о многочленах.
Постепенное расширение области натуральных чисел до совокуп ности всех действительных чисел было вызвано необходимостью сде лать выполнимыми во всех случаях без исключения известные опера ции деления, вычитания, установления соответствия между числами и отрезками и др. Аналогично этому, введение комплексных чисел обу словлено, например, требованием, чтобы всякому алгебраическому уравнению можно было приписать вполне определенное решение.
Чтобы получить решение квадратного уравнения х2 1 0, необхо димо ввести новые символы i и i при условии, что i2 1.
2.17. Комплексные числа |
129 |
Читатель, безусловно, имеет знакомство с комплексными числами. Тем не менее мы здесь обращаем внимание на одно особенно важное соотношение, связанное с геометрическим и тригонометрическим способами изображения комплексных чисел, и приводим необходи мые сведения о корнях многочлена.
2.17.1. Комплексные числа. Определение, геометрическое изображение
ОПРЕДЕЛЕНИЕ 1. Комплексным числом называется выражение вида z a bi, где a и b — действительные числа, i — мнимая единица: i 
 1, i2 1. a — действительная часть числа z (a Re z), b — мни мая часть (b Im z). Если a 0, то число z ib — чисто мнимое, если b 0, то z a — действительное число.
1, i2 1. a — действительная часть числа z (a Re z), b — мни мая часть (b Im z). Если a 0, то число z ib — чисто мнимое, если b 0, то z a — действительное число.
Два комплексных числа, z a bi и z a bi, отличающиеся только знаком мнимой части, называются сопряженными.
Комплексные числа z1 a1 ib1, z2 a2 ib2 называются равными,
если a1 a2 , b1 b2 . Комплексное число z 0, если a 0, b 0.
2.17.2. Геометрическое изображение комплексных чисел
M62
поставить в соответствие
Как известно, каждой паре чисел a и b можно некоторую точку плос
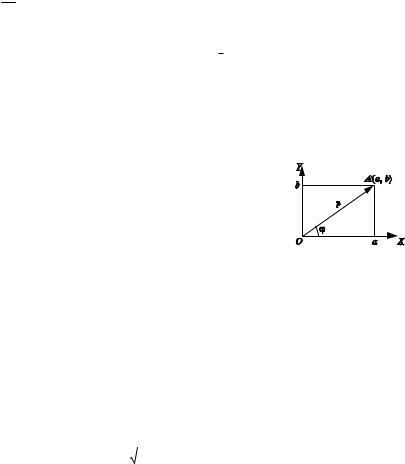
кости или вектор с координатами {a, b}. В соот ветствии с этим, удобно каждому комплексному
числу z a bi поставить в соответствие точку
A(a, b) плоскости X0Y или вектор 0А. Если b 0, то комплексное число лежит на оси 0Х; 0Х — дей
ствительная ось. Если a 0, то число чисто мнимое, лежит на оси 0Y. 0Y — мнимая ось. Плоскость X0Y здесь — комплексная плоскость.
2. Тригонометрическая форма комплексного числа. Обозначим через r и ( полярные координаты точки A(a, b), считая начало коорди нат полюсом, а положительное направление оси 0Х — полярной осью. Тогда
za bi r (cos ( i sin ()
—тригонометрическая форма записи комплексного числа. r — модуль комплексного числа, ( — аргумент:
r | z|, |
( arg z; |
|||||
|
|
|
( arctg |
b |
. |
|
r a2 b2 , |
||||||
|
||||||
|
|
|
|
a |
||

130 Глава 2. Дифференциальное исчисление функций одной переменной
Аргумент, очевидно, вычисляется с точностью до 2'k. Сопряженные числа имеют одинаковый модуль и отличающийся знаком аргумент:
| z| | z |, arg z arg z.
Действительное число также может быть записано в тригонометриче
ской форме: |
|
A | A |(cos0 i sin 0), |
A 0, |
A | A |(cos ' i sin '), |
A 0. |
2.17.3. Действия над комплексными числами
Сложение. Суммой двух комплексных чисел z1 a1 b1i, z2 a2 b2i называется комплексное число, определяемое равенством:
z1 z2 (a1 a2) (b1 b2)i. |
(1) |
Из (1) следует, что сложение комплексных чисел, изображенных век торами, производится по правилам сложения векторов.
|
|
|
|
|
|
|
|
|
|
M62 |
|
|
|
|
b1i и z2 a2 b2i |
|||||||||||
Вычитание. Разностью комплексных чисел z1 a1 |
||||||||||||||||||||||||||
называется число, определенное равенством |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z1 z (a1 a2) i(b1 b2). |
|
|
|
|
|
|
||||||||||
Умножение комплексных чисел производится по правилу умноже |
||||||||||||||||||||||||||
ния многочленов с учетом того, что i2 1: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
z1 z2 (a1 ib1)(a2 ib2) a1a2 ib1a2 ia1b2 b1b2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(a1a2 b1b2) i(a1b2 a2b1). |
|
|
|
|
|
|
||||||||||
Пусть комплексные числа заданы в тригонометрической форме: |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z1 r1(cos (1 i sin (1), |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
z2 r2(cos (2 i sin (2), |
|
|
|
|
|
|
|
|
|
|||||||
z1z2 r1r2 [(cos (1 cos (2 sin (1 sin (2) i(sin (1 cos (2 cos (1 sin (2)] |
||||||||||||||||||||||||||
|
|
|
|
|
|
r1r2[cos((1 (2) i sin ((1 (2)]. |
|
|
|
|
(2) |
|||||||||||||||
Если числа z |
и |
|
|
|
|
сопряженные, то |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
(a bi)(a bi) a2 b2 | z|2 . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
zz |
|
|
|
|
|
|
|||||||||||||||
Деление. Пусть требуется разделить два комплексных числа: |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z1 a1 b1i, |
z2 a2 b2i; |
|
|
|
|
|
|
|||||||||||
|
z1 |
|
a1 b1i |
|
(a1 b1i)(a2 b2i) |
|
a1a2 b1b2 |
i |
a2b1 a1b2 |
. |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
z |
|
a b i |
|
|
|
|
|
a |
2 |
b |
2 |
|
a |
2 |
b |
2 |
|
|
a |
2 |
|
b |
2 |
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
2 |
2 |
2 |
|
|
2 |
|
2 |
|
||||||||||||
