
Основы высшей математики для инженеров 2009
.pdf
|
1.4. Векторное и смешанное произведение |
|
|
|
21 |
||||||||||
Геометрический смысл смешанного произведения: |
|
|
|
|
|||||||||||
a, b, c Va, b, c — объем параллелепипеда, построенного на век |
|||||||||||||||
торах a, b, c, если векторы a, b, c образуют правую тройку; |
|
||||||||||||||
a, b, c Va, b, c |
— если a, b, c образуют левую тройку. |
|
|||||||||||||
Доказательство. |
Для |
определенности |
|
|
|
|
|
|
|
|
|||||
рассмотрим случай правой тройки векто |
|
|
|
|
|
|
|
|
|||||||
ров a, b, c (pис. 1.12). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычисление смешанного произведения |
|
|
|
|
|
|
|
|
|||||||
в прямоугольной системе координат |
|
|
|
|
|
|
|
|
|
||||||
Пусть в прямоугольной системе ко |
|
|
|
|
|
|
|
|
|||||||
ординат |
|
|
|
|
|
|
|
|
|
|
Рис. 1.12 |
|
|
||
a (x1, y1, z1), |
b (x2, y2, z2), |
c (x3, y3, z3). |
|
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
k |
y |
z |
x |
z |
x |
y |
# |
|
|
|||
[a, b] x |
y |
z |
|
|
|||||||||||
|
1 |
1 |
, |
1 |
|
1 , |
1 |
1 |
$, |
|
|
||||
|
1 |
1 |
1 |
y2 |
z2 |
x2 z2 |
x2 |
y2 % |
|
|
|||||
|
x2 |
y2 |
z2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y1 z1 y |
x1 z1 z |
|
|
|
|
x1 |
y1 |
z1 |
||||
a, b, c ([a, b], c) x |
|
x1 |
y1 x |
y |
z . |
||||||||||
|
|
3 |
y |
z |
3 |
x |
z |
3 |
x |
y |
|
2 |
2 |
2 |
|
|
|
|
M622 2 |
|
2 |
2 |
|
x3 |
y3 |
z3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, |
|
|
|
|
x1 |
y1 |
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a, b, c x2 |
|
y2 z2 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
x3 |
y3 |
z3 |
|
|
|
|
|
|
|
|
Свойства смешанного произведения: |
|
|
|
|
|
|
|
|
|
||||||
1)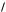 a, b, c
a, b, c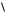 0 a, b, c образуют правую тройку;
0 a, b, c образуют правую тройку;
2)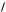 a, b, c
a, b, c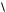
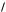 b, c, a
b, c, a
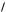 c, a, b
c, a, b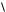 — это вытекает из геометрическо го смысла смешанного произведения;
— это вытекает из геометрическо го смысла смешанного произведения;
3)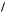 a, b, c
a, b, c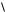
 b, a, c
b, a, c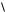
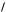 c, b, a
c, b, a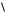 — доказать самостоятельно.
— доказать самостоятельно.
1.4.4.Приложения смешанного произведения
1.Вычисление объемов параллелепипеда и пирамиды:
Vпар  a, b, c
a, b, c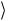
 ,
,
V |
|
1 |
S |
|
h |
1 |
S |
|
h |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, b |
, |
|
|
. |
||||||||||
тр |
пар |
a |
c |
|||||||||||||||||
|
|
|
||||||||||||||||||
пир |
3 |
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

22Глава 1. Элементы линейной алгебры и аналитической геометрии
2.Смешанное произведение позволяет проверить компланарность трех векторов:
a, b, c компланарны Vпар 0  a, b, c
a, b, c 0.
0.
3. Смешанное произведение позволяет выяснить, когда 4 точки лежат в одной плоскости:
A (x1, y1, z1), B(x2, y2, z2), C (x3, y3, z3), D(x4, y4, z4) лежат в од
ной плоскости AB, AC, AD — компланарны
|
|
|
|
|
|
x2 x1 |
y2 y1 |
z2 z1 |
|
AB, AC, AD 0 |
x3 x1 y3 y1 z3 z1 |
. |
|||||||
|
|
|
|
|
|
x4 x1 |
y4 y1 |
z4 z1 |
|
Векторное и смешанное произведение применяются в механике и физике. Поэтому очень важно в совершенстве овладеть этими поня тиями.
1.5. ПрямаяM62и гиперплоскость
Прямая в Rn. Гиперплоскость в Rn. Взаимное расположение прямой и ги перплоскости. Расстояние от точки до гиперплоскости.
1.5.1. Прямая в Rn
Будем рассматривать n мерное пространство действительных чисел Rn{x} x (x1, x2, , xn), xi R}
со стандартным ортонормированным базисом
e1 (1, 0, , 0), e2 (0, 1, , 0), , en (0, 0, , 1) и скалярным произведением
(x, y) x1y1 x2 y2 xn yn.
Вектор с координатами (0, 0, …, 0) назовем точкой 0. Эта точка вме сте с базисом, отложенным от этой точки, будут образовывать пря
моугольную систему координат |
в Rn. Под произвольной |
точкой |
|||
M Rn с координатами (x , x , , x ) мы будем понимать |
радиус |
||||
|
|
1 |
2 |
n |
|
вектор 0M (x1, x2, , xn).

1.5. Прямая и гиперплоскость |
23 |
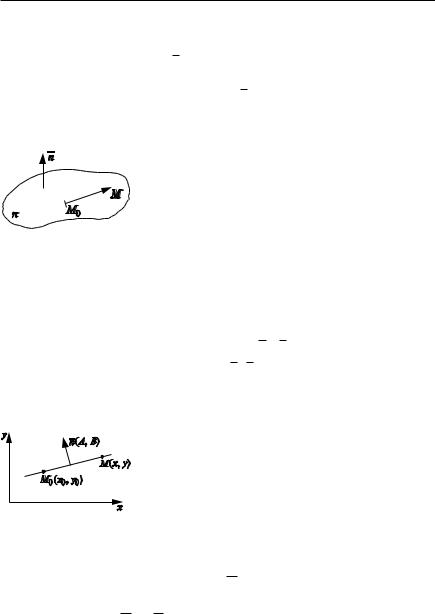
ОПРЕДЕЛЕНИЕ 1. Прямой l в пространстве Rn, проходящей через точку M0 параллельно вектору a, называется множество всех точек M Rn, для которых вектор M0M коллинеарен a (pис. 1.13).
M(x1, x2, , xn) l M0M || a
M0M ta rM rM 0 ta.
|
|
|
|
|
|
|
|
|
|||||
Отсюда rM rM 0 ta — векторное уравнение пря |
|||||||||||||
мой |
t R |
. |
|
|
|
|
Рис. 1.13 |
||||||
Записывая векторное уравнение прямой в координатах, получим |
|||||||||||||
параметрические уравнения прямой: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
x0 |
ta , |
|
|
|
|
|
|
|
|
|
|
|
& 1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
&x |
x0 |
ta |
, |
t R. |
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
&. . . . . . . . . |
|
|||
|
|
|
|
|
|
|
|
|
& |
x0 |
ta |
, |
|
|
|
|
|
|
|
|
x1 |
x |
|
||||
|
|
|
|
|
|
|
x1Mx2 x622 xn xn |
||||||
|
|
|
|
|
|
|
|
|
n |
n |
n |
|
|
Выражая из каждого уравнения параметр t, получим канонические уравнения
0 |
0 |
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a1 |
a2 |
|
|
an |
|
|
|
|
|
|||
ОПРЕДЕЛЕНИЕ 2. Под углом между прямыми l1 и l2 понимается |
|||||||||||||
угол между их направляющими векторами |
|
|
|
|
: (l1,^l2) ( |
|
^ |
|
|
||||
a1, a2 |
a1, a2). |
||||||||||||
Задача 1. Написать уравнение прямой, проходящей через точку M0(1, 1) параллельно a (1, 0).
Решение. Напишем каноническое уравнение
x 1 y 1 y 1 0.
10
Задача 2. Написать уравнение прямой, проходящей через две точ ки M1(x1, y1), M2(x2, y2).
Решение. Вектор M1M2 (x2 x1, y2 y1) можно взять в качестве направляющего, поэтому уравнение имеет вид
x x1 |
|
y y1 |
. |
|
|
||
x2 x1 |
y2 y1 |
||
24 Глава 1. Элементы линейной алгебры и аналитической геометрии
1.5.2. Гиперплоскость в Rn
Пусть в Rn заданы точка M0(x10, , xn0) и вектор
n (A1, A2, , An).
ОПРЕДЕЛЕНИЕ 3. Гиперплоскостью ' в Rn, проходящей через точку M0 перпендикулярно вектору n, называется множество всех
точек M Rn, для которых вектор |
M0M |
|
|
|
. Вектор |
|
называется нор |
|||||||||||||||||||
|
n |
n |
||||||||||||||||||||||||
мальным вектором плоскости '. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Выведем уравнение плоскости ': |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
M(x1, x2, , xn) ' M0M |
|
(M0M, |
|
) 0 |
||||||||||||||||||
|
|
|
|
n |
n |
|||||||||||||||||||||
|
|
|
|
A |
(x |
x0) A (x |
x |
0) A |
(x |
x0) 0 |
||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
1 1 |
1 |
2 |
2 |
2 |
|
|
|
|
|
n |
|
n |
|
n |
|||||||
|
|
|
|
— |
|
линейное |
уравнение |
гиперплоскости |
||||||||||||||||||
|
|
Рис. 1.14 |
(pис. 1.14). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Это уравнение можно записать так: |
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
где |
|
|
|
A1x1 A2 x2 An xn b 0, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
b (A x0 A x0 |
|
A x0) const. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
1 |
2 |
|
|
n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ОПРЕДЕЛЕНИЕ 4. Углом между плоскостями ' |
и ' |
называется |
|||||||||||||||||||||||
|
|
|
|
|
M62 |
1 |
|
2 |
|
|
|
|
||||||||||||||
угол между их нормальными векторами n1, n2 :
|
|
|
|
('1,^'2) (n1,^n2). |
|
Частные случаи |
|
|
|
||
1. |
n 2, |
R2. |
|
|
|
|
|
|
|
A(x x0) B(y y0) 0# |
|
|
|
|
|
или |
& |
|
|
|
|
$ |
|
|
|
|
|
Ax By C 0 |
& |
|
|
|
|
% |
|
|
|
|
— линейные уравнения гиперплоскости (прямой) |
||
|
|
|
в R2 |
(pис. 1.15). |
|
|
Рис. 1.15 |
Проведем исследование уравнения Ax By C 0: |
|||
|
|
|
|||
1) B 0 Ax C 0 |
|
|
|||
x C ; A
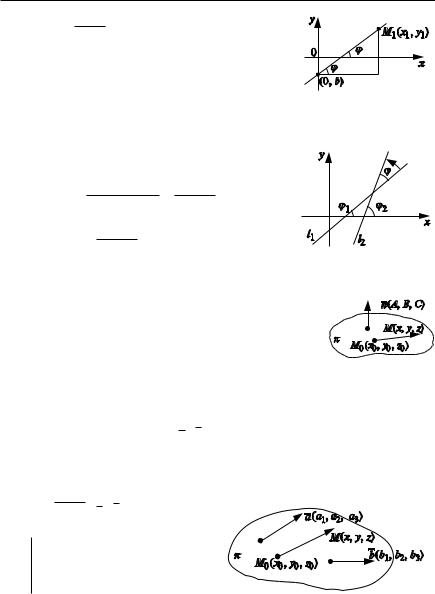
2) В 0 y A x C kx b; y kx b — уравнение прямой с
BB
угловым коэффициентом (pис. 1.16).
|
|
1.5. Прямая и гиперплоскость |
25 |
|||
Здесь tg ( |
y1 b k, так как y |
kx b . Итак, |
|
|||
|
|
x1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
угловой коэффициент k — это тангенс угла |
|
|||||
наклона прямой к положительному направле |
Рис. 1.16 |
|||||
нию оси 0x. |
|
|
|
|
||
Задача 3. Найти угол между прямыми, заданными уравнениями с |
||||||
угловыми коэффициентами (pис. 1.17). |
|
|||||
( (l1,^l2) (2 (1 tg ( tg ((2 (1) |
|
|||||
|
tg (2 tg (1 k2 k1 . |
|
|
|||
|
|
1 tg (1 tg (2 |
1 k1k2 |
|
|
|
Итак, tg (l ,^l ) |
k2 k1 . В частности, |
|
|
|||
1 |
2 |
1 k2 k1 |
|
|
|
|
|
|
|
|
|
Рис. 1.17 |
|
|
l1 l2 k1k |
1. |
|
|
2. |
n 3, R3 |
M62& |
||
(рис. 1.18). |
|
|
||
|
A(x x0) B(y y0) C(z z0) 0# |
|||
|
|
или |
|
$ |
|
|
Ax By Cz |
D 0 |
& |
|
|
% |
||
— линейные уравнения плоскости в R3.
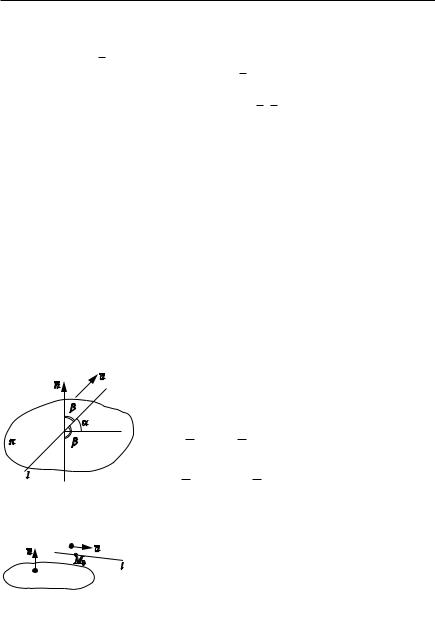
Задача 4. Написать уравнение плоскости в R3, проходящей через точку и два неколлинеарных вектора (pис. 1.19).
Решение. M ' M0M, a, b — компланарные векторы. Если три вектора лежат в одной плоскости, то их смешанное произведение рав но нулю. Из этого условия и получаем уравнение плоскости при дан ных условиях:
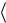 M0M, a, b
M0M, a, b 0
0
x x0 y y0 z z0 |
|
||
a1 |
a2 |
a3 |
0. |
b1 |
b2 |
b3 |
|
Рис. 1.19
26 Глава 1. Элементы линейной алгебры и аналитической геометрии
1.5.3. Взаимное расположение прямой и гиперплоскости
Даны прямая l, проходящая через точку M0(x10, x20, , xn0) парал
лельно вектору a (a1, a2, , an), и гиперплоскость ': A1x1 A2 x2
An xn b 0 с нормальным вектором n (A1, A2, , An).
1. Прямая l и гиперплоскость ' пересекаются в одной точке, если прямая не параллельна плоскости, т.е. (a, n) 0.
Точку пересечения гиперплоскости и прямой M1 можно найти, ре шив линейную систему из n 1 уравнения с n 1 неизвестными x1,
x2, , xn, t: |
|
|
|
|
|
|
|
|
|
|
|
|
A1x1 A2 x2 An xn b 0, |
|
|
||||||||
|
& |
x0 |
a t, |
|
|
|
|
|
|
|
|
|
&x |
|
|
|
|
|
|
|
|||
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
& |
x0 |
a t, |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
&. . . . . . . . . |
|
|
|
|
|
|
|
|||
|
& |
x0 |
|
|
|
|
|
|
|
|
|
|
&x |
a t. |
|
|
|
|
|
|
|
||
|
n |
n |
n |
|
|
|
|
|
|
|
|
a (x0 |
|
M62 |
|
|
|
|
|
|
|||
a t) |
a (x0 a t) a (x0 a t) b 0. |
||||||||||
1 1 |
1 |
|
|
|
n |
n |
n |
|
|
||
Пусть t1 — решение последнего уравнения. Тогда точка пересече |
|||||||||||
ния ' и l имеет координаты x |
x0 |
a t, , |
x |
x0 |
a t. |
||||||
|
|
|
1 |
1 |
1 |
n |
|
n |
|
n |
|
|
|
Задача 5. Найти угол между прямой и гипер |
|||||||||
|
плоскостью (pис. 1.20). |
|
|
|
|
|
|
||||
|
|
Решение. ) (l,^'), |
* ( |
|
,^ |
|
). |
||||
|
|
n |
a |
||||||||
* ' ) ' * sin ) cos * | cos *|.
22
* ' ) * ' sin ) cos * | cos * |.
Рис. 1.20 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
всегда sin ) | cos * | |
|( |
|
|
, |
|
|
|
)| |
. |
||||||||||||||
|
Итак, |
a |
n |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
| |
|
| | |
|
| |
|
|||||||||||||
|
|
|
|
|
|
|
a |
n |
|||||||||||||||||
|
2. Прямая l параллельна гиперплоскости ' |
||||||||||||||||||||||||
|
|
M0 ', |
|
|
|
|
( |
|
, |
|
) 0, |
|
M0 '. |
||||||||||||
|
|
a |
n |
a |
n |
|
|||||||||||||||||||
|
3. Прямая |
l принадлежит |
гиперплоскости |
||||||||||||||||||||||
Рис. 1.21 |
' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
M0 ' ( |
|
, |
|
|
) 0, |
|
M0 '. |
||||||||||||
|
|
|
a |
|
n |
a |
n |
|
|||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
1.5. Прямая и гиперплоскость |
|
|
|
|
|
27 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
1.5.4. Расстояние от точки до гиперплоскости |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Пусть нам даны гиперплоскость ' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
A1x1 A2 x2 An xn b 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
с нормальным вектором |
|
|
|
(A1, A2, , An) и точкa |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
M |
|
(x0, |
x0, , |
|
x0) '. Под расстоянием от точки |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
0 |
1 |
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0 до плоскости ' мы будем понимать длину пер |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
пендикуляра |
M0M : | M0M | +(M0, ') (pис. 1.22). |
|
|
|
|
Рис. 1.22 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|( |
n |
, |
M0M )| | |
n |
| | M0M | cos ( |
n |
, M0M ) | |
n |
| | M0M | |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
A |
(x x0) A (x x0)| |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
+(M0, ') | M0M | |
|
1 1 |
|
1 |
|
|
|
|
|
|
|
|
n n |
|
|
|
n |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|(A x0 |
A x |
0 A x |
0 b) (A x A x A x b)| |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 1 |
2 2 |
|
|
|
|
|
|
|
|
|
|
n n |
|
|
|
|
|
1 1 |
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
n n |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| A x0 A x0 A x0 |
b| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, окончательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A x0 |
|
A x0 A x0 b| |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
+(M0, ') |
|
|
1 |
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
n n |
|
|
. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Задача 6. |
Показать, |
|
что |
|
прямые l1: x 2 y 4 0 и l2:2 x 4y 3 0 |
|||||||||||||||||||||||||||||||||||||||||||||||
параллельны, и найти расстояние между ними. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Решение. l1||l2 n1 (1, 2)|| n2 |
(2, 4) |
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
Точка M0(0, 2) l1. Очевидно, что расстояние |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
+(l , l ) |
+(M |
0 |
, l ) |
|
|2 0 |
4 ( 2) 3| |
|
11 |
. |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 16 |
|
2 |
5 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Умение аналитически описывать прямую и плоскость дает воз можность моделировать эти геометрические объекты, не прибегая к их натуральному воспроизведению.

28 Глава 1. Элементы линейной алгебры и аналитической геометрии
1.6. Матрицы и операции над ними
Основные определения. Операции над матрицами. Определитель квадратной матрицы. Обратная матрица.
1.6.1. Основные определения
ОПРЕДЕЛЕНИЕ 1. Матрицей A размера m ! n называется прямо угольная таблица чисел, расположенных в m строках и n столбцах
|
a11 |
a12 |
|
a1n |
|
|
|
|
|
A |
a21 |
a22 |
a2n . |
|
|
|
|
|
|
|
|
aт2 |
|
|
|
aт1 |
aтn |
||
Числа aij (i 1, , m; j i, , n) называются элементами матри цы A. Первый индекс i указывает номер строки, а второй j — номер столбца, на пересечении которыхM62расположен элемент aij . Сокращен ное обозначение матрицы A (aij)m!n. Матрица A (aij) размера n ! n называется квадратной. Матрица размера m !1 называется вектором столбцом:
a1
Aa2 .
am
Нулевая матрица — это матрица, все элементы которой равны 0. Единичная матрица порядка n — это квадратная матрица n го поряд ка вида
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
E |
0 |
1 |
|
0 |
. |
|
|
|
|||
0 0 1
Понятие матрицы оказалось очень удобным для компактной за писи и обработки объемной информации. Матрицы и матричные обозначения применяются почти во всех разделах математики и, в частности, в теории линейных систем, численных методах, диф ференциальных уравнениях, теории вероятностей. Понятие матрицы было введено в работах английских математиков У. Гамильтона
1.6. Матрицы и операции над ними |
29 |
и А. Кэли в середине XIX в. Основы теории созданы немецкими ма тематиками К. Вейерштрассом и Ф. Фробениусом (вторая половина XIX в. и начало ХХ в.)
1.6.2.Операции над матрицами
1.Равенство матриц.
ОПРЕДЕЛЕНИЕ 2. |
Две матрицы A (aij), B (bij) совпадают |
| A B|, если совпадают их размеры и соответствующие элементы рав |
|
ны, т. е. при всех i, j |
aij bij. |
2. Сложение матриц.
ОПРЕДЕЛЕНИЕ 3. Суммой двух матриц A (aij)m!n и B (bij)m!n одинаковых размеров называется матрица C (cij)m!n A B тех же размеров, элементы которой определяются равенствами cij aij bij .
Например, |
|
|
|
|
|
|
|
|
|
|
|
1 2 3 |
, |
1 0 |
|
|
0 2 5 |
||||||
A |
5 |
|
B |
1 |
0 |
2 |
|
C A B |
5 |
. |
|
|
|
|
|
|
|
|
|||||
4 |
6 |
|
|
|
5 |
4 |
|||||
3. Умножение матрицыM62на число. |
|
|
|||||||||
ОПРЕДЕЛЕНИЕ 4. Произведением матрицы A (aij)m!n на числоR называется матрица B (bij)m!n A, элементы которой опреде ляются равенствами bij aij .
4. Умножение матриц.
ОПРЕДЕЛЕНИЕ 5. Произведением матрицы A (aij)m!k на мат
рицу B (bij)k !n называется матрица C (cij)m!n A B размера m ! n, элементы которой cij определяются равенством
cij ai1b1j ai2b2 j aikbkj.
Таким образом, элемент матрицы C A B, расположенный в i й строке и j м столбце, равен сумме произведений элементов i й строки матри цы A на соответствующие элементы j го столбца матрицы B. Например,
|
2 |
3 |
1 |
|
2 |
1 |
1 |
|
|
а) |
, |
|
|
2 |
|
|
|||
A |
|
|
B 1 3 |
|
|
||||
|
1 |
0 |
|
|
|
|
|
|
|
|
1 2 !3 |
|
|
2 |
1 |
|
|
||
|
|
|
|
|
0 |
3!3 |
|
||

30 Глава 1. Элементы линейной алгебры и аналитической геометрии
C AB |
2 2 3 1 1 0 2 1 3 3 1 2 |
2 ( 1) 3( 2) 1 1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
0( 2) |
|
|||
|
|
1 2 0 1 1 0 1 1 0 3 1 2 1 ( 1) |
1 1 |
|
||||||||||
|
|
|
|
|
|
7 |
13 7 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
0 2 !3 |
|
|
|
|
||
б) |
1 0 |
, |
B |
0 0 |
0 0 |
0 0 |
BA, |
|
|
|||||
A |
|
|
|
AB |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
т. е. произведение матриц не обладает свойством коммутативности.
5. Транспонированные матрицы.
ОПРЕДЕЛЕНИЕ 6. Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров. Полученная матрица обозначается через A . Например,
|
1 |
2 |
1 |
3 |
2 |
|
|
|
|||
A |
3 1 |
A |
1 |
. |
|
|
|
|
|
4 2 !3 |
|
|
2 4 3! |
|
|
|
|
Квадратная матрица называется симметричной, если A A , т. е. |
|||||
|
|
M62 |
|
||
для элементов выполнены равенства aij |
a ji. |
|
|||
1.6.3. Определитель квадратной матрицы
Определитель (число) квадратной матрицы порядка n A (aij)n!n обозначается символами
|
a11 |
a12 |
a1n |
|
|
det A | A| |
a21 |
a22 |
a2n |
. |
|
|
|
|
|
|
|
|
an1 |
an2 |
|
ann |
|
Вычисление определителя будет дано индуктивно по порядку матри цы. Для матрицы 2 го порядка ее определитель положим равным
| A | |
a11 |
a12 |
a a a a . |
|||
|
a21 |
a22 |
11 |
22 |
21 |
12 |
|
|
|
|
|
||
