
Основы высшей математики для инженеров 2009
.pdf
3.10. Вычисление длины дуги кривой |
181 |
Эта сумма является интегральной суммой для функции 1 f 2(() на [), *] 2
и ее предел при max -(i 0 есть определенный интеграл. Поэтому ис комая площадь равна
|
|
|
1 |
|
* |
1 |
* |
|
|
|
|
|
S |
|
D+2 d( |
D[f (()]2 d(. |
|||||
|
|
2 |
2 |
|||||||
|
|
|
|
) |
) |
|
|
|||
|
|
|
|
|
|
|
|
|||
П р и м е р. Вычислить |
площадь, ограниченную кардиоидой |
|||||||||
r a(1 cos(). |
|
|
|
|
|
|
|
|
||
|
1 |
2' |
1 |
2' |
|
|
3 |
|
||
S |
Dr2 d( |
Da2(1 cos()2 d( |
'a2 (ед2). |
|||||||
|
2 |
|
|
|||||||
2 |
0 |
|
0 |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|||
3.10. Вычисление длины дуги кривой
Вычисление длины дуги M62в декартовых координатах. Вычисление длины дуги в случае параметрического задания кривой. Длина дуги в поляр ных координатах.
|
3.10.1. Вычисление длины дуги в декартовых координатах |
||||||||
|
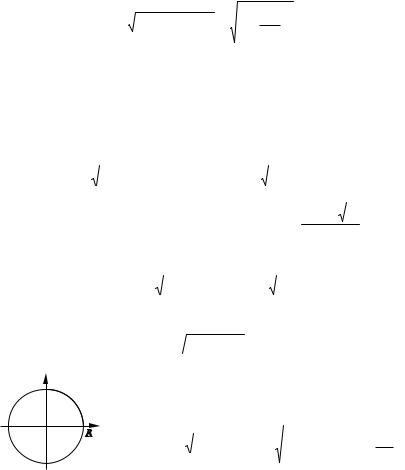
Пусть в прямоугольных координатах на плоскости задана дуга |
||||||||
уравнением y f (x). Найдем длину части этой дуги, заключенной ме |
|||||||||
жду вертикальными прямыми x a, x b. Вспомним определение дли |
|||||||||
ны дуги. Разобьем [a, b] на n частей точка |
|
||||||||
ми |
x0 a, |
x1, x2 , |
|
…, |
xn b. |
Положим |
|
||
A f (a), |
M1 f (x1), |
…, |
Mn 1 f (xn 1), |
|
|||||
B f (b). Соединим точки А, …, В отрезками |
|
||||||||
прямой |
и |
получим |
|
ломаную |
|
||||
AM1M2 Mn 1B, вписанную в дугу АВ. |
|
||||||||
Длины ее звеньев |
обозначим |
через -S1, |
Рис. 3.15 |
||||||
-S2 , …, -Sn. Тогда длина ломаной |
|||||||||
|
|||||||||
n
Sn F-Si. i 1
3.10. Вычисление длины дуги кривой |
183 |
3.10.2. Вычисление длины дуги в случае параметрического задания кривой
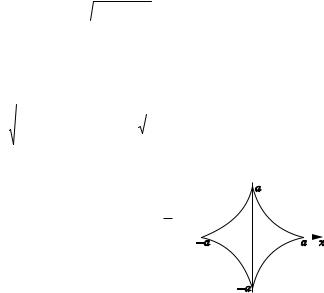
Пусть кривая задана параметрическими уравнениями x ((t), y >(t), где t [), *]. Пусть на [), *] функции ((t) и >(t) непрерывно дифференцируемы, причем ((t) 0 на [), *]. В этом случае параметри ческие уравнения определяют некоторую функцию y f (x) на [a, b], где a (()), b ((*). Длина дуги кривой, заключенной между прямыми x a, x b, вычисляется по формуле
b
S D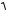 1 [f (x)]2 dx.
1 [f (x)]2 dx.
|
|
|
|
|
a |
|
|
|
|
|
Сделаем замену переменной: |
|
|
>(t) |
|
|
|||||
x ((t), |
|
dx ((t)dt, |
f (x) |
. |
||||||
|
||||||||||
|
|
|
|
|
|
|
((t) |
|||
Тогда |
|
|
|
|
|
|
|
|
|
|
* |
|
7>(t):2 |
* |
|
|
|
|
|||
|
|
|
|
|
||||||
S D |
1 9 |
|
< ((t)dt D [( (t)]2 >(t)]2 dt. |
|||||||
|
||||||||||
|
8 |
((t); |
|
|
|
|
|
|||
) |
|
|
M62 |
|||||||
|
|
|
|
) |
|
|
|
|
||
П р и м е р. Вычислить длину дуги астроиды x a cos3 t, y a sin3 t. Астроидa симметрична относительно коор 
динатных осей, поэтому считаем 1/4 длины ее дуги. При этом параметр t меняется от 0 до ' .
|
|
|
2 |
|
xt 3a cos2 t sint, yt 3a sin2 t cost, |
|
|
||
' |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
S 4D3a cost sint dt 6a. |
|
Рис. 3.17 |
||
0 |
|
|
|
|
3.10.3. Длина дуги кривой в полярных координатах
Пусть в полярных координатах задано уравнение кривой + f ((), где ( [), *].
Перейдем от полярных координат к декартовым:
x + cos(, |
y + sin (. |
(3) |
Выражая + через ( и подставляя в (3), получим
x +(() cos(, |
y +(() sin (. |

184 |
Глава 3. Интегральное исчисление функций одной переменной |
Последние соотношения можно рассматривать как параметрическое задание кривой. Тогда
*
S D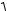
 (x()2 (y()2 d(,
(x()2 (y()2 d(,
)
x(2 y(2 (+ cos( + sin ()2 (+ sin ( + cos()2 + 2 +2.
Таким образом,
*
S D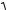
 +2 + 2 d(.
+2 + 2 d(.
)
3.11. Вычисление объема. Механические приложения определенного интеграла
Вычисление объема тела по известным поперечным сечениям. Объем тела вращения. ВычислениеM62работы переменной силы. Задача на вы числение давления.
3.11.1. Вычисление объема тела по известным поперечным сечениям
Рассмотрим некоторое тело, объем которого нужно определить. Предположим, что нам известна площадь каждого сечения этого тела плоскостью, перпендикулярной некоторой оси (оси OX). Эти сечения называются поперечными. Таким образом, площадь поперечного се чения есть функция одного аргумента x. Обозначим ее S (x). Через a и b обозначим абсциссы крайних сечений тела. Разобьем [a, b] на n
частей точками x0 a, x1, x2 , …, xn b. На каждом участке [xi 1, xi] вы берем точку Ai: xi 1 Ai xi. Через точки деления xi проведем плоско
сти перпендикулярно оси OX. При этом тело разобьется на n слоев. Через точки Ai также проведем сечения.
С одной стороны,
n
VF-Vi,
i 1
где -Vi — объем i го слоя. Объем i го слоя можно считать приближен но равным объему прямого цилиндра с образующей, параллельной


186 |
Глава 3. Интегральное исчисление функций одной переменной |
3.11.2. Объем тела вращения
Рассмотрим криволинейную трапецию с основанием [a, b], огра ниченную непрерывной кривой y f (x), и найдем объем тела, образо ванного вращением этой трапеции вокруг оси OX. Каждое поперечное сечение — круг, следовательно, его площадь S (x) '[f (x)]2 . Тогда по
формуле (2)
b
V ' D[f (x)]2 dx.
a
Если тело вращения получено вращением криволинейной трапе ции вокруг оси OY, то можно показать, что объем тела может быть
найден по формуле
b
V 2' D xf (x)dx.
a
П р и м е р. Найти объем тела, полученного вращением параболы y x2 , x [0, 1] вокруг оси OX и оси OY.
|
1 |
M62 |
|
|
||
V1 |
' D x4dx |
' ; |
V ' D x x2 dx |
' |
. |
|
|
0 |
|
5 |
0 |
2 |
|
|
|
|
|
|
||
3.11.3. Вычисление работы переменной силы
Пусть под действием переменной силы F материальная точка дви жется по прямой OX от точки x a до x b, причем направление силы совпадает с направлением движения. Если F const, то работа силы
A F(b a).
У нас же F F(x).
Разобьем [a, b] на n частей точками x0 a, x1, …, xn 1, xn b. В ка ждой части выберем Ai: xi 1 Ai xi. Заменим работу силы на участке
-xi xi xi 1 приближенно работой постоянной силы F(Ai). Тогда
-Ai F(Ai)-xi,
nn
An F-Ai FF(Ai)-xi.
i 1 i 1
An — интегральная сумма для F(x) на [a, b]. Предел этой суммы при max -xi 0 существует и равен работе силы на [a, b]:
nb
A lim |
FF(Ai)-xi DF(x)dx. |
|
max -xi 0 i 1 |
a |
|

3.11. Вычисление объема… |
187 |
П р и м е р. Удлинение пружины -l пропорционально приложен ной силе F
-l kF,
где l — ее первоначальная длина, k – коэффициент жесткости пружи ны и задан равным 0,001 м/H. Вычислить работу силы F при растяже нии данной пружины на 5 см.
Решение. Пусть U — перемещение точки приложения силы F к концу пружины. Тогда для каждого фиксированного положения при статическом (достаточно медленном, когда можно пренебречь силами инерции пружины) растяжении пружины имеем
F u . k
На последующем удлинении пружины на du совершается работа dA Fdu.
Вся работа при совершении заданного удлинения -l будет
-l |
-l |
u |
|
u2 |
-l |
1 |
|
|
A DFdu D |
|
du |
|
|
|
|
F(-l)-l. |
|
|
|
|
|
|||||
|
M62 |
|
||||||
0 |
0 |
k |
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
||
Таким образом, при статическом нагружении пружины силой F работа равна половине произведения окончательного значения этой силы на окончательное значение перемещения точки приложения силы. Дан ный вывод носит название теоремы Клапейрона.
С учетом условий данного примера получим
F(-l) |
0,05 |
H 50 H |
A |
1 |
50 0,05 Н м 1,25. |
|
|
||||
0,001 |
2 |
|
|||
3.11.4. Задача на вычисление силы Архимеда
Рассмотрим задачу о вычислении выталкивающей силы, действую щей на тело, погруженное в жидкость (силы Архимеда). В качестве примера возьмем пирамиду со стороной b квадратного основания и высотой H, погруженную в жидкость вершиной вниз на всю высо ту Н. Так что плоскость основания находится на уровне поверхности жидкости. Введем координатную ось х, направленную вниз с началом отсчета на поверхности жидкости. Тогда давление жидкости р на по верхность пирамиды определяется по формуле
p +gx,
где + — плотность жидкости; g — ускорение свободного падения.
188 |
|
Глава 3. Интегральное исчисление функций одной переменной |
|||||||||||
|
|
|
|
|
|
|
|
|
Выделим четырехгранный |
пояс поверхности |
|||
|
|
|
|
|
|
|
|
|
пирамиды двумя плоскостями x1 x и x2 x dx |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
(рис. 3.19). Сила давления dP |
на каждую грань |
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
этого пояса равна произведению давления р на |
||||
|
|
|
|
|
|
|
|
|
площадь поверхности одной грани пояса: |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
dP pb(x) |
dx |
, |
b(x) 2(H x)ctgB, |
|
|
|
Рис. 3.19 |
|||||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
sinB |
|
|
|
где b(x) — размер стороны поперечного сечения пирамиды, B — угол между внешней нормалью к поверхности боковой грани и осью х, он равен двугранному углу при основании пирамиды. Выталкивающая сила dFa, обусловленная силами давления на грани этого пояса, равна сумме проекций сил давления dP на вертикаль:
dFa 4dP cosB 4+gx b(x)ctgB dx.
Теперь можно вычислить всю силу Fa, создаваемую давлением жидко
сти на грани пирамиды:
Fa HD 8+g ctgM6B x(H x)dx24+g ctg2B G3, 3
0
ctgB |
b |
, |
Fa 1 |
+gb2 H. |
|
||||
|
2H |
3 |
|
|
Еще раз подтверждается, что выталкивающая сила равна весу вытес ненной жидкости.
3.12. Несобственные интегралы
Интегралы с бесконечными пределами (несобственные интегралы пер вого рода). Теоремы сравнения для несобственных интегралов первого рода. Интегралы от разрывных функций (интегралы второго рода). Тео ремы сравнения для несобственных интегралов второго рода.
«Интегральное исчисление немного бы стоило, если бы первооб разная не разыскивалась в конечном виде, но всегда требовала бы тоже перехода к пределу; в этом случае не было бы никакого прогресса… Вся огромная заслуга Ньютона и Лейбница состояла именно в конечной выразимости результата фактически невыполнимой операции… С тех
3.12. Несобственные интегралы |
189 |
пор минуло более 250 лет и по пути Ньютона и Лейбница прошло нема ло сильных людей. Никто из них не смог продолжать дело основопо ложников анализа бесконечно малых и не мог указать другого метода выражать в конечном виде результат суммирования бесконечно ма лых… Лишь на долю Коши, сильнейшего аналитика XIX века, выпала честь дать особый прием, названный им исчислением вычетов, с помо щью которого во многих случаях, там, где отказывает испытанный ме тод первообразных Ньютона и Лейбница, можно выражать в конечном виде результат суммирования бесконечно большого числа бесконечно малых слагаемых» (Лузин Н. Н. Исаак Ньютон как математик и натура лист (1943)).
3.12.1. Интегралы с бесконечными пределами (несобственные интегралы первого рода)
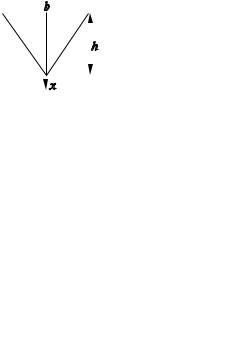
Пусть функция f (x) определена и непрерывна при всех значени ях x таких, что a x M62. Рассмотрим интеграл
b
J(b) D f (x)dx.
a
При изменении b этот интеграл меняется и является непрерывной функцией b. Рассмотрим вопрос о поведении этого интеграла при b .
ОПРЕДЕЛЕНИЕ. Если существует конечный предел
b
lim J(b) lim D f (x)dx,
b b a
то этот предел называется несобственным интегралом 1 го рода от a до и обозначается символом
D f (x)dx.
a
Таким образом,
b
D f (x)dx lim D f (x)dx.
a b a

 1 [
1 [