
Основы высшей математики для инженеров 2009
.pdf
|
1.12. Классификация кривых и поверхностей второго порядка |
|
|
61 |
||||||||||||||||||
Пусть e1, e2 — ортонормированный базис из собственных векторов |
||||||||||||||||||||||
оператора А; 1, 2 — собственные значения. Если |
|
|
|
|
|
|||||||||||||||||
|
|
e1 )11i )21 j, |
|
|
e2 )12i )22 j, |
|
|
|
|
|
||||||||||||
то положим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
) |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
12 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
)21 |
)22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
причем векторы e1 и e2 возьмем в таком по |
|
|
|
|
|
|
|
|
|
|||||||||||||
рядке, что |B| 0. Тогда переход от прямо |
|
|
|
|
|
|
|
|
|
|||||||||||||
угольной системы координат (0, i, j) к пря |
|
|
|
|
|
|
|
|
|
|||||||||||||
моугольной системе координат (0, e1, e2) |
|
|
|
|
|
|
|
|
|
|||||||||||||
будет |
осуществляться |
|
путем |
|
поворота |
|
|
|
Рис. 1.44 |
|
|
|
||||||||||
(pис. 1.44). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть (x, y) и (x , y ) — координаты точки М в базисе i, |
j и e1, e2 |
|||||||||||||||||||||
соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Покажем, что переход от старых координат к новым осуществляет |
||||||||||||||||||||||
ся по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
(3) |
||||
|
|
|
|
|
|
|
|
y |
B |
|
|
; |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
M62 |
|
|
|
|
|
|
|
|
|
|||||||
|
OM xi yj x e1 y e2 x ()11i )21 j) y ()12 i )22 j) |
|
||||||||||||||||||||
|
|
(x )11 y )12)i (x )21 y)22) j, |
|
|
|
|
|
|||||||||||||||
т. е. |
x |
|
11 x )12 y |
|
|
|
)12 x |
x |
|
|
|
|
||||||||||
|
) |
)11 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
. |
|
|
|
|
|
|
y |
)21 x |
)22 y )21 )22 |
y |
y |
|
|
|
|
|
||||||||||||
Покажем, что в новых координатах квадратичная форма не будет |
||||||||||||||||||||||
содержать произведения x y : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a11x2 2a12 xy |
a22 y2 |
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
A |
|
|
, |
(A OM, OM) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
y |
|
|
|
|
|
|
|
|
|
|
|
(A(x e1 y e2), x e1 y e2) (x Ae1 y Ae2, x e1 y e2) |
|
|
|||||||||||||||||||
|
(x 1e1 y 2 e2, x e1 y e2) (x )2 1(e1, e1) x y 1(e1, e2) |
|
||||||||||||||||||||
|
|
2 |
2 |
(e1, e2) 1(x |
|
2 |
|
2 |
|
1 |
0 x |
x |
||||||||||
(x y ) 2(e1, e2) (y ) |
|
) 2(y ) |
|
|
|
|
|
|
, |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
y |
|
y |
|

62 Глава 1. Элементы линейной алгебры и аналитической геометрии
Итак, после поворота (3) квадратичная форма (2) запишется в виде
1(x )2 2(y )2,
где 1, 2 — собственные значения оператора А, и мы свели задачу к уже рассмотренному частному случаю.
П р и м е р. Привести к каноническому виду уравнение кривой
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 xy |
|
2 x |
|
2 y 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1. Запишем матрицу квадратичной формы и найдем ее собствен |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ные значения и собственные векторы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 2 1 0 |
|
|
|
|
|
|
|
|
1, |
|
|
1; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
||||||||||||||
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 1 x |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t |
x |
1 |
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y 0 |
|
|
|
|
|
|
|
|
|
t |
; |
||||||||||||||||||||||||||
1 |
|
|
|
1 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y t |
|
y |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||||||||||||
|
1 |
1 1 x |
|
|
|
|
|
0 |
x y |
0 |
|
|
x t |
x |
1 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
. |
|||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y t |
|
|
|
y |
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0: |
|
|
|
1 |
|
||||||||||||||||
и запишем матрицу |
|
|
|
|
|
|
|
|
M62 |
|B| |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Итак, векторы |
a1 |
(1, 1), |
a2 |
( 1, 1) |
образуют базис из собственных век |
||||||||||||||||||||||||||||||||||||||||||||||||||
торов, отвечающих собственным значениям 1 1, 2 1. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Получим из собственных векторов |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
a1, a2 единичные векторы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
поворота В так, чтобы |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
a1 |
|
1 |
|
|
(1, 1), |
|
|
|
|
|
|
|
|
a2 |
|
|
( 1, 1), |
|
|
|
||||||||||||||||||||||||||||
|
e |
|
|
|
|
|
|
|
e |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
1 |
|
|
| a1| |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
| a2| |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|B| 1 0. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. С помощью матрицы поворота В осуществим в уравнении кри вой переход от старых координат к новым, используя (3):
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
2 |
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 xy 2 x 2 y |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
y |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
y |
|
x |
y |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x y x y |
|
|
|
|
|
|
|
x y |
|
|
|
x y |
(x )2 |
(y )2 |
2 x 0. |
||||||||||||||||||||||||||
2 |
|
2 |
|
|
2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
1.12. Классификация кривых и поверхностей второго порядка |
63 |
4. Выделим полные квадраты у членов, содержащих x и y :
(x )2 2 x 1 1 (y )2 0 (x 1)2 (y )2 1.
Сделаем замену x x 1, y y (x )2 (y )2 1.
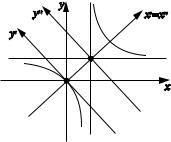
Получаем каноническое уравнение гиперболы с асимптотами x y , x y (pис. 1.45).
Рис. 1.45 |
1.12.2. Классификация поверхностей второго порядка
Теорема 2. Всякая поверхность второго порядка в R3 является или эллипсоидом, или однополостным гиперболоидом, или двуполостным ги2 перболоидом, или эллиптическим параболоидом, или гиперболическим па2 раболоидом, или конусом, илиM62эллиптическим цилиндром, или гиперболиче2 ским цилиндром, или параболическим цилиндром, или парой пересекаю2 щихся плоскостей, или парой параллельных плоскостей, или парой совпа2 дающих плоскостей, или прямой, или точкой, или пустым множеством.
Приведение уравнения поверхности второго порядка
a11x2 2a12 xy a22 y2 2a31xz 2a23 yz a33z2 b1x b2 y b3z b0 0
к каноническому виду осуществляется так же, как в двумерном случае. Матрица квадратичной формы здесь имеет вид
a |
a |
a |
|
11 |
12 |
13 |
|
A a21 |
a22 |
a23 . |
|
|
a32 |
a33 |
|
a31 |
|
||

ГЛАВА 2
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
2.1. Введение в математический анализ
Элементы теории множеств. Действительные числа. Понятие предела числовой последовательности. Арифметические действия с последо вательностями, имеющими предел.
Математический анализ — часть математики, в которой функции и их обобщения изучаются на основе теории пределов. В него входят дифференциальное исчисление, интегральное исчисление, теория обыкновенных дифференциальных уравнений, теория дифференци альных уравнений с частными производными и т. д. Современная тео рия чисел и теория вероятностейM62применяют и развивают методы ма тематического анализа.
Все же термин «математический анализ» часто употребляется для наименования только основ математического анализа, объединяющих в себе теорию действительного числа, теорию пределов, теорию рядов, дифференциальное и интегральное исчисление и их непосредствен ные приложения.
При изучении явлений природы и общества, технических процес сов мы сталкиваемся с изменением величин, с функциональной зави симостью одной из величин от другой. Поэтому понятие о перемен ной величине является основным в математическом анализе, отсю да — его объективная важность как средства изучения функций.
Под переменной величиной мы будем понимать величину, которая принимает хотя бы два различных значения. Величина, которая не ме няет своего значения, называется постоянной.
2.1.1. Множества вещественных чисел
Основным в математике является также понятие множества, т. е. совокупности каких либо объектов произвольной природы. Объекты, входящие в данное множество, будем называть элементами множества.

2.1. Введение в математический анализ |
65 |
Обозначения: множества A, B, …, X, Y, элементы a, b, …, x, y, x A (x принадлежит А), A , B (А — подмножество В), 0 — пустое множество.
Множество натуральных чисел N {1, 2, …, n, …} появилось в свя зи со счетом предметов. Затем под влиянием потребностей практики, развития самой математики были введены целые числа Z {…, –1,
m#
0, 1, …} и рациональные числа Q  $, где m, n Z, n 0, причем
$, где m, n Z, n 0, причем
n%
дробь m несократима. Введение рациональных чисел, однако, не ре n
шило важной практической задачи измерения отрезков. Например, диагональ квадрата со стороной 1 есть 
 2. В связи с этим появились иррациональные числа. Рациональные и иррациональные числа назы ваются действительными или вещественными.
2. В связи с этим появились иррациональные числа. Рациональные и иррациональные числа назы ваются действительными или вещественными.
Неравенства для абсолютных величин.
Неравенство | a| 1 эквивалентно неравенствам 1 a 1, если
| a b| 1 b 1 a b 1. |
|
|
|
|
|
Справедливы следующие неравенства. |
|
|
|||
1. |
| a b| | a| |b|. |
M62 |
|
||
2. |
| a b| | a| |b|. |
|
|
|
|
Доказательство. 1. |
a b 0 | a b| a b, но |
a | a|, b |b| |
|||
| a b| | a| |b|. |
|
|
|
|
|
a b 0 | a b| a b, |
но |
a | a | | a |, |
b | b| |b| |
||
| a b| | a| |b|. |
|
|
|
|
|
2. |
| a b| | a| |b|. |
|
|
|
|
a (a b) b | a | | a b| |b| | a b| | a | |b|.
Отрезок, интервал, ограниченное множество.
Пусть числа a, b удовлетворяют неравенству a b. Множество x : a x b — отрезок [a, b].
Множество x : a x b — интервал (открытый отрезок) (a, b). Множества x : a x b, a x b — полуинтервалы.
Часто встречаются бесконечные интервалы: [a, ) (a, ), ( , ). Произвольный интервал (a, b), содержащий точку c: a c b, называ ется окрестностью с. В частности, интервал c 1, c 1) (1 0) 1 — ок рестность c.
Пусть X {x} — произвольное множество действительных чисел. Говорят, что X ограничено сверху, если существует ( ) действительное

66 Глава 2. Дифференциальное исчисление функций одной переменной
число М такое, что для любого ( )x X : x M, и ограничено снизу, если m: x X x m. Множество Х ограничено, если оно ограниче но и снизу, и сверху, т. е. M : x X | x| M.
2.1.2. Понятие предела числовой последовательности
Пусть натуральному числу n 1, 2, … по некоторому правилу или закону поставлено в соответствие действительное число xn. Тогда го ворят, что задана числовая последовательность x1, x2,
{xn} {x1, x2, }.
Говорят также, что переменная xn пробегает значения последователь но {xn}.
П р и м е р ы.
1. |
|
1 |
|
1 |
# |
1# |
M62 |
||
1, |
|
, |
|
, $ |
|
|
$. |
|
|
2 |
3 |
|
|
||||||
|
|
|
% |
n% |
|
||||
2. |
{ 1, 2, |
3, 4, } {( 1)nn}. |
|||||||
ОПРЕДЕЛЕНИЕ 1. Число a называется пределом последователь ности {xn}, если 1 0 зависящее от 1 положительное число N0 N0(1) такое, что | xn a | 1 для всех n N0. Символически сходи мость последовательности {xn} к числу а записывается равенством
|
|
|
|
|
|
lim xn a или xn a, n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
Если xn a n N, то, очевидно, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
lim xn a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
П р и м е р ы. |
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
1 |
0 |
|
|
1 |
1 или |
|
1. |
lim |
|
0. В самом деле, зададим 1 0. Тогда |
|
|||||||||
|
n |
|
|||||||||||
|
|
n n |
|
|
|
n |
|||||||
1 |
n n0 |
1 |
. |
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|||||
Поэтому lim 1 0.
n n

2.1. Введение в математический анализ |
67 |
|
Неравенство | xn a | 1 эквивалентно |
следующим |
неравенствам: |
1 xn a 1 или a 1 xn a 1, т. е. |
xn 1 — |
окрестности: |
xn (a 1, a 1). |
|
|
Таким образом, определение предела можно дать так: a — предел числовой последовательности {xn}, если 1 0 n0: все точки xn с n n0 попадут в 1 окрестность точки a : xn (a 1, a 1).
Теорема 1. Если переменная xn имеет предел, то он единственный.
Доказательство. Пусть |
|
|
|
|
|
|
|
|
lim |
xn a 1 |
0 |
n1: n n1 |
| xn a | |
1 |
, |
||
|
|
|||||||
n |
|
|
|
2 |
|
|
||
lim |
xn b 1 |
0 |
n2: n n2 |
| xn b| |
1 |
|
||
|
||||||||
n |
|
|
|
2 |
|
|||
| a b| | a xn (b xn)| | a xn| |b xn| 1, n n0 max (n1, n2) a b.
Теорема 2. Если последовательность {xn} имеет предел, то она ог2 раничена. M62
Доказательство. Пусть lim xn a и пусть
n0 n0(1): | xn a | 1 (n n0).
Но | xn| | a | | xn a | | xn| 1 | a | n n0. |
|
|
Пусть M max {1 a, | x1|, | x2 |
|, , | xn |
|} M | xn| n. |
|
0 |
|
2.1.3. Арифметические действия с последовательностями, имеющими предел
Пусть заданы две последовательности: {xn}, {yn}. Рассмотрим после
|
|
|
|
|
|
|
# |
|
довательности {x |
y }, |
{x |
y }, |
{x |
y }, |
|
xn |
$. |
|
||||||||
n |
n |
n |
n |
n |
n |
yn% |
||
|
|
|
|
|
|
|||
Справедливы следующие утверждения.
1. lim (xn / yn) lim xn / lim yn.
n
2. lim
n
3. lim
n
(xn yn) lim xn lim yn.
xn lim xn , если lim yn 0. yn lim yn

68 Глава 2. Дифференциальное исчисление функций одной переменной
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
|
lim |
xn a 1 0 |
n1: | xn |
a | |
1 |
, |
|
|
|
|
|||||
|
|
|
(n |
|
max (n , n )); |
|||||||||||
|
|
n |
|
|
|
2 |
|
|
||||||||
|
|
lim |
yn b 1 0 |
n2: | yn |
b| |
1 |
|
|
0 |
1 |
2 |
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
n |
|
|
|
2 |
|
|
|
|
|
|
||||
| xn yn (a / b)| | xn a | | yn b| |
1 |
|
1 |
1. |
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||
П р и м е р. x ( 1)n — нет предела, |
|
|
|
|
||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
n |
( 1)n 1 — нет предела, но |
lim (x |
y ) |
0; lim x y |
1. |
||||||||||
|
|
|
|
|
|
|
|
|
n |
n |
|
n |
n |
|||
2.2.Числовые последовательности
Онеопределенностях. Монотонные последовательности. Число å. Верх няя и нижняя границы множеств. Теорема Больцано – Вейерштрасса.
2.2.1M62. О неопределенностях
При изучении теорем о пределах последовательностей мы не рас сматривали последовательности, имеющие бесконечно большие пре делы, а также случай, когда при отыскании предела частного предел стоящей в знаменателе последовательности равен нулю.
П р и м е р ы. |
|
|
|
|
|
|
||
1. xn n2 n |
xn yn n . |
|
|
|
||||
yn n2 , |
|
|
|
|||||
|
|
|
|
|
|
|||
2. xn n2 n |
xn yn 3. |
|
|
|
|
|||
yn n2 3 , |
|
|
|
|
||||
|
|
|
|
|
|
|||
3. xn n2 |
1 |
|
0. |
|
|
|||
yn n2 |
1 |
, |
xn yn |
|
|
|
|
|
n |
|
|
||||||
|
|
|
|
|
||||
|
n |
|
|
|
|
|
|
|
4. xn n2 |
xn yn ( 1) |
n |
— не имеет предела. |
|||||
yn n2 ( 1)n , |
|
|
|
|
||||
Рассмотренные примеры показывают, что сумма двух бесконечно больших последовательностей разных знаков может стремиться к лю бому числу, к бесконечности, а также вообще не иметь предела.

2.2. Числовые последовательности |
69 |
В этом случае говорят, что имеет место неопределенность вида ( , ). Аналогично могут встречаться другие неопределенности:
если |
|
x |
, |
y |
, то |
|
|
x |
n |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
n |
|
|
n |
|
|
|
|
|
|
|
y |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
если |
|
x |
0, |
y |
0, то |
|
|
|
n |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
n |
|
n |
|
|
|
|
|
|
|
y |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
если |
|
xn 0, |
yn , |
то |
|
|
xn yn(0, ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
П р и м е р. |
|
|
|
|
|
|
nm a n a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
a |
m |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n b nk b n b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a) m k: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
amnm a1n a0 |
|
|
|
|
|
|
|
a |
m |
a |
|
|
1 |
|
a |
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 nm |
|
|
|
|||||||||||||||||||||||||
lim |
|
lim |
|
|
|
|
|
|
1 nm 1 |
|
|
am |
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
n b nk b n b |
|
|
|
|
|
|
n |
b |
b |
|
|
1 |
|
b |
|
1 |
|
|
bk |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
k |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
k |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
1 |
|
n |
0 |
n |
|
|
|
||||||||
в) m k: |
|
|
|
|
M62k 1 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
б) m |
k: |
|
|
|
|
|
|
|
nm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
lim |
a |
m |
a n a |
0 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
n b nk b n b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
m |
nm a n a |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n b nk |
b n b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.2.2. Монотонные последовательности. Определение
Последовательность {xn} называется неубывающей (невозрастаю щей), если n N
xn xn 1 (xn xn 1).
Неубывающие (невозрастающие) последовательности называются монотонными.
Теорема. Монотонная ограниченная последовательность всегда име2 ет предел. Данное утверждение — наглядно очевидное, и мы, прини мая его без доказательства, рассмотрим пример его использования при построении алгоритма вычисления предела бесконечной числовой по следовательности, которая сходится к иррациональному числу е.

70 Глава 2. Дифференциальное исчисление функций одной переменной
2.2.3. Число e
Рассмотрим последовательность |
|
|
|
|
1 |
n# |
|
& |
& |
||
{xn} 1 |
|
|
$. |
|
|||
& |
n |
& |
|
|
|
|
% |
Покажем, что эта последовательность — возрастающая и ограничен ная сверху. По формуле бинома Ньютона
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
n(n 1) (n k |
1) 1 |
|
|
|
|
|
|
|
|
|
|
n(n 1) 1 1 |
|
||||||||||||||||||||||||||||||||
xn 1 |
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
nn |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
1 |
n(n 1) |
1 |
|
|
|
1 |
|
|
|
n(n 1) (n k 1) |
|
1 |
|
n(n 1) (n n 1) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
nn |
|
|
|
|
|
|
||||||||||||||||
2 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
k 1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
n 1 |
|
||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
. |
|
|||||||||||||||||||||||||||||||||||
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2! |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
n! |
|
|
n |
|
|
n |
|
|||||||||||||||||||||||||||||||||
xn 2 |
1 |
|
1 |
2 |
|
1M61 21 1 1 1 1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как видим, |
xn 2 |
|
|
|
n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Докажем, что последовательность ограничена сверху. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2! |
|
|
|
|
|
n! |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2k 1 |
2n 1 |
|
|
|
2 |
|
|
|
|
|
2n |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Покажем, что последовательность возрастающая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
xn 1 2 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
n |
xn, |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
(n 1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
1 |
|
|
|
|
|
n 1 |
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
так как каждое слагаемое больше z, кроме того, у xn 1 на одно слагае
мое больше. По предыдущей теореме существует lim xn:
n
|
|
1 n |
||
lim 1 |
|
|
|
e; |
|
||||
n |
|
n |
|
|
2 e 3, e 2,718281828… .
Число e было впервые предложено Эйлером.
