
Основы высшей математики для инженеров 2009
.pdf
2.7. Введение в дифференциальное исчисление функций одной переменной… 91
Далее,
|
-(uv) (u -u)(v -v) uv u-v v-u -u-v; |
|
|
|
|||||
(uv) lim |
-(uv) |
|
lim |
u-v v-u -u-v |
uv vu |
lim |
-u lim |
-v |
. |
|
|
|
|||||||
-x 0 -x |
-x 0 |
-x |
-x 0 |
-x 0 -x |
|||||
Но lim -u 0, так как функция u непрерывна, как функция, имею
-x 0
щая предел, и -u
Далее,
u v
v
0. Поэтому (uv) u v uv .
lim |
u -u u |
|
1 |
|
lim |
v-u u-v |
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
||||||||
-x 0 |
v -v v |
|
-x -x 0 (v -v)v-x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
-u |
|
u |
-v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
u v uv |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
lim |
|
|
|
|
-x |
-x |
|
, |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
-x 0 |
(v -v)v |
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|||||||||||||
3. (sin x) cos x. |
|
M62 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
так как -v 0 |
при -x |
0, потому что v имеет производную, и следо |
|||||||||||||||||||||||||||||||
вательно, непрерывна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin |
-x |
cos |
|
-x |
|||||
|
|
|
|
sin (x -x) sin x |
|
|
|
|
|
|
|
|
x |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||
(sin x) |
lim |
|
|
|
lim |
|
|
|
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
-x |
|
|
|
|
|
|
|
|
|
|
-x |
|
|
|
||||||||||||||
|
-x 0 |
|
|
|
|
|
|
|
-x 0 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
sin |
-x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
lim |
2 |
|
|
|
lim cos |
|
1 cos x. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
-x 0 |
|
-x |
|
|
-x 0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. (cos x) sin x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. (tg x) |
|
1 |
|
|
sec2 x; (tg x) |
sin x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
cos2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
6. (ctg x) cosec2 x |
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

92 Глава 2. Дифференциальное исчисление функций одной переменной
7. (loga x) |
1 |
loga e |
|
1 |
|
. (x 0): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
|
|
x ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-x |
|
|
|
|
|
|
|
-x |
|||||
|
-y |
|
|
|
log (x -x) log |
|
x |
|
|
log |
a |
1 |
|
|
|
|
|
1 |
|
log |
a |
1 |
|
|
|||||||||||||
|
|
|
|
|
|
x |
|
x |
|||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
y loga x; |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
-x |
|
|
|
-x |
|
|
|
|
|
|
|
|
|
|
-x |
|
|
|
|
x |
|
|
|
-x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
-x |
x |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
-x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
loga 1 |
|
|
|
|
|
|
|
|
|
|
loga e |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
x |
|
|
x |
|
-x 0 x |
|
|
|
|
|
х ln a |
|
|
|
|
|
|
|
|
|||||||||||||
Вчастности,
8.(ln x) 1 . x
2.8. Производные сложных,M62обратных, логарифмических функций
Производная сложной функции. Обратная функция и ее производная. Про изводные элементарных функций и степенно показательных выражений.
2.8.1. Производная сложной функции
Теорема. Если функция u ((x) имеет производную в точке x, а функ2 ция y f (u) — в точке u, то сложная функция y F(x) f [((x)] имеет производную по x в точке x и F (x) f (u)((x).
Доказательство. Зададим -x 0, |
тогда -u ((x -x) ((x). Если |
|||||
-u 0, то |
|
|
||||
|
-y |
|
-y |
|
-u |
. |
|
|
|
|
|||
|
-x -u |
-x |
||||
При -x 0, -u 0 (в силу непрерывности ((x), как имеющей произ водную). Поэтому yx yu ux.
Таким образом, производная сложной функции равна произведе нию производной данной функции по промежуточному аргументу на производную промежуточного аргумента.

2.8. Производные сложных, обратных, логарифмических функций |
93 |
2.8.2. Обратная функция
Рассмотрим функцию y x3, x [ 1, 2] (рис. 2.16). Область значе ний этой функции есть отрезок [–1, 8]. Функция x 3 y, отображаю щая отрезок [–1, 8] в [–1, 2], называется обратной к функции y x3. Некоторые функции не имеют обратных. Например, y x2 , при x ( , ), т. к. каждому значению y 0 соответствуют два значения
y, отображаю щая отрезок [–1, 8] в [–1, 2], называется обратной к функции y x3. Некоторые функции не имеют обратных. Например, y x2 , при x ( , ), т. к. каждому значению y 0 соответствуют два значения
x /
 y. Если y f (x), то обратную функцию можно обозначить через x f 1(y).
y. Если y f (x), то обратную функцию можно обозначить через x f 1(y).
ОПРЕДЕЛЕНИЕ. Функция y f (x) называет ся возрастающей на некотором сегменте (или ин тервале), если для x2 x1 f (x2) f (x1). Функция y f (x) называется убывающей, если для x2 x1 f (x2) f (x1).
Если f (x) является только возрастающей или |
|
|
убывающей на некотором сегменте, то она моно |
Рис. 2.16 |
|
тонна на нем. |
M621 |
|
|
|
|
Теорема существования обратной функции. Если y f (x) непрерывна на [a, b] и монотонна на нем, то на соответствующем сегменте оси OY существует обратная функция x f (y), которая также является не2 прерывной монотонной функцией.
Производная обратной функции.
Теорема. Пусть y f (x) монотонна и дифференцируема в некотором интервале и имеет в точке x производную f (x) 0. Тогда обратная функция дифференцируема, и
[f 1(y)] 1 . f (x)
Доказательство. Так как y f (x) монотонна, дифференцируема (а значит, непрерывна), то x f 1(y) существует, монотонна и непре рывна. Зададим -y 0, тогда x f 1(y) получит приращение -x, кото рое в силу монотонности отлично от нуля. Так как x f 1(y) непре
рывна, то -x 0 при -y 0, следовательно, |
|
|
|
||||
[f 1(y)] lim |
-x |
lim |
1 |
|
|
1 |
. |
|
-y |
|
|
||||
-y 0 -y -x 0 |
|
f (x) |
|||||
-x

94Глава 2. Дифференциальное исчисление функций одной переменной
2.8.3.Производные элементарных функций
1
1. (arcsin x)  .
.  1 x2
1 x2
y arcsin x. Рассмотрим функцию x sin y. Она монотонна и диф ференцируема при ' y ' , x cos y 0 — в этом интервале. Тогда
22
|
|
y |
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
cos y |
|
|
|
|
2 |
1 |
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
1 sin |
y |
x |
|
|
|
|
|||||||||||
2. (arctg x) |
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y arctg x, y |
|
|
' |
|
, |
' |
, при этом обратная функция x tg y моно |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
тонна и дифференцируема, |
|
dx |
|
|
|
|
1 |
; |
dy |
cos2y |
1 |
|
1 |
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
dy |
|
cos2y |
dx |
1 tg2 y |
1 x2 |
||||||||||||||||||||||||||||||
Аналогично: |
|
|
|
|
1 x2 M62 |
|
|
|
|
|
|
|||||||||||||||||||||||||
3. (arccos x) |
|
|
|
|
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4. (arcctg x) |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. (ax) ax ln a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y ax, x loga y — обратная, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
y |
1 |
|
|
|
|
1 |
|
|
|
y ln a ax ln a. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
xy |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y ln a
В частности,
(ex) ex.
6. (x)) )x) 1 () — произвольное действительное число).
y x) e)ln x,
y e)ln x ) 1 x) ) 1 )x) 1.
xx

|
|
|
2.9. Дифференциал |
95 |
|||
2.8.4. Дифференцирование степенно>показательных выражений |
|||||||
Пусть y u(x)v(x). Тогда ln y v (x) ln u(x). |
|
|
|||||
Продифференцируем обе части данного соотношения: |
|
|
|||||
|
y |
1 |
|
7 |
u (x): |
||
|
|
v (x) ln u(x) v(x) |
|
u (x) y y |
9v (x) ln u(x) v(x) |
|
<. |
|
|
u(x) |
|
||||
|
y |
|
8 |
u(x) ; |
|||
П р и м е р.
y xx; y y(ln x 1) xx(ln x 1).
2.9. Дифференциал
Дифференциал функции. Связь между существованием производной и существованием дифференциала функции. Свойства дифференциала. Дифференциал сложной функции. Инвариантность формы первого диф ференциала. Геометрический смысл дифференциала. Его применение в приближенных вычисленияхM62. Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически.
2.9.1. Дифференциал функции
Рассмотрим функцию y x2 .
-y (x -x)2 x2 x2 2 x-x -x2 x2 2 x-x (-x)2.
Таким образом, первое слагаемое линейно относительно -x. (-x)2 — бесконечно малая более высокого порядка, чем 2 x-x:
lim (-x)2 lim -x 0.
-x 0 2 x-x -x 0 2 x
Поэтому первое слагаемое — главная часть приращения функции. Пусть задана функция y f (x) и пусть
-y f (x -x) f (x) A-x )(-x), |
(1) |

96 Глава 2. Дифференциальное исчисление функций одной переменной
где А — постоянное число, не зависящее от -x, а )(-x) — бесконечно малая более высокого порядка, чем -x, т. е.
lim |
)(-x) |
0. |
(2) |
|
|||
-x 0 |
-x |
|
|
ОПРЕДЕЛЕНИЕ. Если приращение функции y f (x) в точке x может быть представлено в виде (1), то главная часть A-x, линейная относительно -x, называется дифференциалом функции.
С и м в о л и к а: dy A-x или d(f (x)) A-x. Приращение независи мой переменной -x называется ее дифференциалом: -x dx.
2.9.2. Связь между существованием производной и существованием дифференциала функции
Теорема 1. Если функция f (x) имеет в точке x производную, то она |
||||||
|
M6f (x) |
2. |
||||
имеет в этой точке и дифференциал. |
|
|
||||
Доказательство. |
|
|
|
|
|
|
|
|
|
lim |
|
-y |
|
|
|
|
|
-x 0 -x |
||
По теореме о представлении функции, имеющей предел, |
||||||
|
|
-y |
f (x) *(-x), |
|||
|
|
|
||||
|
|
-x |
|
|
|
|
где lim *(-x) 0. Но тогда -y f (x)-x *(-x) -x и |
||||||
-x 0 |
|
|
|
|
|
|
|
|
lim |
*(-x)-x |
0, |
||
|
|
|
||||
|
|
-x 0 |
-x |
|
|
|
следовательно, по определению f (x) имеет в точке x дифференциал d(f (x)) f (x)-x.
Теорема 2. Если f (x) имеет в точке x дифференциал, то она имеет в этой точке и производную.
Доказательство. -y A-x )(-x) -y A )(-x)
|
|
-x |
-x |
lim |
-y |
A 0 A A f (x). |
|
|
|||
-x 0 |
-x |
|
|

2.9. Дифференциал |
97 |
Итак, dy f (x)-x f (x) dx. Следовательно, f (x) dy, т. е. производ dx
ная равна отношению ее дифференциала к дифференциалу независи мой переменной.
З а м е ч а н и е. На основании вышеизложенного можно ввести второе определение производной как отношение дифференциалов:
y 4x5 dy . dx
2.9.3. Свойства дифференциала
Пусть u(x) и v(x) — дифференцируемые функции. Тогда d(u v) du dv,
d(uv) udv vdu,
|
|
|
|
|
|
|
d |
u |
|
vdu udv |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
v |
|
v |
|
|
|
|
|
|||
В самом деле, например,M62 |
|
|
||||||||||||||||
u |
u |
|
u v v u |
|
(u dx)v (v |
dx)u |
du v dv u |
. |
||||||||||
d |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
v2 |
|
|
v2 |
||||||||
v |
v |
|
|
|
|
|
|
|
|
|
|
|||||||
2.9.4. Дифференциал сложной функции
Пусть y f (x), x ((t), |
т. е. y f [((t)]. Тогда |
||
dy y dt |
y x dt y dx |
f (x)dx. |
|
t |
x t |
x |
|
Таким образом, дифференциал сложной функции y f [((t)] имеет тот же вид dy f (x)dx, какой он имел бы в случае, если бы промежу
точный аргумент был независимой переменной. |
|
|
|||||||
П р и м е р. y sin |
|
, или y sin u, u |
|
, dy cos |
|
|
1 |
|
dx, сле |
x |
x |
x |
|
||||||
|
|
||||||||
2 |
x |
||||||||
довательно, dy cosudи cos
 x d(
x d(
 x).
x).
98Глава 2. Дифференциальное исчисление функций одной переменной
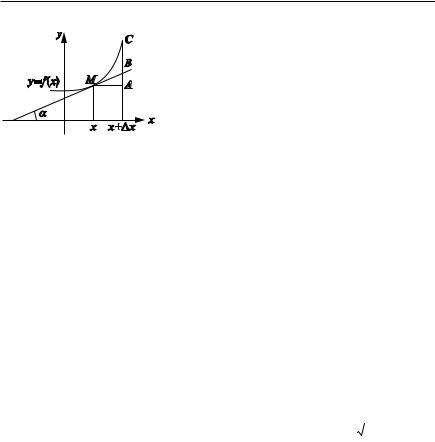
2.9.5.Геометрический смысл дифференциала
Рис. 2.17 |
AC f (x -x) f (x) -y.
AB -x tg ) f (x)-x dy.
АС — приращение функции, АВ — прира щение ординаты касательной к графику функции в точке x, f (x)).
Применение дифференциала в приближенных вычислениях |
|
-y f (x)dx )(-x) dy )(-x). |
|
При достаточно малых -x |
|
-y = dy. |
(*) |
Пусть известно значение функции и ее производной в некоторой точке x0. Тогда
или -y f (M62x0 -x) f (x0) = f (x0)-x f (x0 -x) = f (x0) f (x0)-x.
Таким образом, можно вычислить приближенное значение функции
вточке x0 -x.
Пр и м е р. sin 31" ?
|
f (x) sin x, |
x0 30", |
-x 1" |
|
' |
|
. |
|
|
|
|||
|
180 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
sin (x |
-x) = sin x |
cos x |
-x sin 30" cos30" |
' |
|
|
1 |
|
3 |
0,017 = |
|||
|
|
|
|
||||||||||
0 |
0 |
0 |
|
180 |
2 |
|
2 |
|
|||||
|
|
|
|
|
|
||||||||
=0,5 0,85 0,017 = 0,514.
2.9.6.Производные и дифференциалы высших порядков
Производные высших порядков.
«Если первая производная позволяет нам для данного момента времени описать характер какого либо движения, то вторая помогает проникнуть в его скрытые причины» (Томсон В., Тэт В. Введение в натуральную философию, 1867).

2.9. Дифференциал |
99 |
Пусть на интервале (a, b) задана f (x). Ее производная, если она су ществует на (a, b), есть некоторая функция f (x). Производная от f (x) называется второй производной и обозначается f (x):
f (x) (f (x)) или y (y ) .
Вообще, производной от функции f (x) порядка n называется первая производная от производной от f (x) порядка n 1: f (n)(x) [f (n 1)(x)] .
Для ее существования необходимо существование f (n 1) не только
вточке x, но и в ее некоей окрестности.
Пр и м е р ы. (ex)(n) ex;
(sin x) cos x, (cos x) sin x, (sin x) sin x, (sin x) cos x, .
Дифференциалы высших порядков.
Рассмотрим функцию y f (x); dy f (x)dx. Величину приращения -x dx можно выбирать независимо от точки x. Поэтому dy можно
считать функцией только M62от x. Дифференциал от dy называют вторым
дифференциалом или дифференциалом второго порядка: d2 y d2 f (x), d2 y d(dy).
d2 y d[f (x)dx] [f (x)dx] dx f (x)dx dx f (x)(dx)2.
dn y d(dn 1y) f (n)(x)(dx)n f (n)(x)dxn.
Поэтому
f (n)(x) dn y . dxn
Последняя формула (для n 1) справедлива только в том случае, когда f (x) не является сложной функцией, т. е. только тогда, когда x — неза висимая переменная. Т. е. здесь свойство инвариантности не имеет
места. Однако запись f (n)(x) |
|
|
dn y |
|
|
|
|
|
|
|
|
dn y |
|
|||
|
|
|
сохраняют, рассматривая |
|
|
как |
||||||||||
dxn |
|
dxn |
||||||||||||||
символ, а не отношение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П р и м е р. y sin u, u |
|
x y sin |
|
x. |
|
|
|
|
|
|
|
|||||
dy cosudu; d2 y d(cosu)du cosud2u sin (du)2 cosud2u |
|
|||||||||||||||
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
sin u(du)2 cosu u (dx)2 |
sin u |
|
|
dx2 |
cosu |
|
|
|
(dx)2. |
|||||||
|
|
|
3 |
|
||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
2 |
x |
|
|
|
|
||||||
|
|
|
|
|
4x2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

100Глава 2. Дифференциальное исчисление функций одной переменной
2.9.7.Дифференцирование параметрически заданных функций
x ((t),
t (a, b).
y >(t),
Будем предполагать, что существует обратная функция от x ((t):
t ( 1(x). Тогда |
y >[( 1(x)]. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Будем искать y |
через x , y . В силу инвариантности формы перво |
|||||||||||||||||||||||
|
|
|
x |
|
|
|
|
dy |
t |
|
t |
|
|
|
|
|
|
|
|
|
|
|
||
го дифференциала y |
, но |
dy |
y dt, dx x dt, следовательно, |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
dx |
|
|
|
|
|
t |
|
|
|
|
t |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
yt |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
(x |
|
0). |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
xt |
|
t |
|
|
|
|
|
|
||||
|
|
|
|
|
d yt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d(y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x |
|
|
dy x dx y |
y x dt x y dt |
|
||||||||||||||||
y |
|
x |
|
|
|
|
|
t |
|
|
|
|
t |
t |
|
|
t t |
|
|
t t |
t t |
; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
dx |
|
|
x dt |
|
|
|
|
|
|
2 |
|
dt |
|
3 |
|
||||||||
|
|
|
|
|
|
t |
|
|
|
|
(xt) |
xt |
(xt) dt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
y |
yt xt |
xt yt |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
M62 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
(x )3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
2.10. Некоторые теоремы Ролля, Лагранжа, Коши о дифференцируемых функциях
Теорема Ролля о нулях производной. Теорема Лагранжа о конечных при ращениях. Теорема Коши об отношении приращений двух функций.
2.10.1. Теорема Ролля о нулях производной
Если функция f (x) непрерывна на отрезке [a, b], дифференцируема во всех внутренних точках этого отрезка и на концах отрезка обращается в нуль (т. е. f (a) f (b) 0), то внутри отрезка [a, b] существует по крайней мере одна точка С такая, что f (c) 0.
(Между двумя нулями дифференцируемой функции есть нуль произ2 водной.)
Доказательство. Так как функция f (x) непрерывна на [a, b], то она достигает на этом отрезке своего наибольшего значения М и наимень шего значения m.
Если M m, то f (x) 0 для x [a, b] f (x) 0 для x.
