Математика для инженеров(теория)I том

Очевидно, если существует lim f (x) = b , то существуют и оба

x→a

односторонних предела, причем b совпадает с ними. Справедливо и

b = f (a - 0) = f (a + 0) .

Если же f (a - 0) ¹ f (a + 0) , то lim f (x) не существует.

x→a

30. Предел функции при x → ∞ .

Число b называется пределом функции f (x) при x → ∞ , если для любой бесконечно большой последовательности { xn} соответст- вующая последовательность значений функции { f (xn )} сходится к b

конечно малой при x → a , если lim f (x) = 0 .

x→a

Функция f (x) называется бесконечно большой при x → a ,

если lim f (x) = ¥ .

x→a

1

Например, функция x - 2 есть бесконечно большая функция

при x → 2 .

Имеет место следующее утверждение, характеризующее связь меж- ду бесконечно малыми функциями и бесконечно большими функциями.

Утверждение 1. Для того, чтобы функция f (x) при x → a ( f (x) ¹ 0 при x ¹ a) была бесконечно малой функцией, необходимо и

1

достаточно, чтобы функция f (x) была бесконечно большой функцией при x → a .

243

1

А это и означает, что функция f (x) есть бесконечно большая при

x → a . Обратное утверждение доказывается аналогично. □

Упражнение 1. Определить бесконечно малую и бесконечно большую функции при х ® +¥ и x → −∞ .

Для бесконечно малой функции выполняются те же свойства, что и для бесконечно малых последовательностей (п.2.20).

нечно малая при х ® 1 (свойство 3 из п.2.20). □

20. Связь между функцией, ее пределом и бесконечно малой функцией.

Теорема 1. Для того, чтобы функция f (x) имела предел в точке x = a , равный b, необходимо и достаточно, чтобы функция α (x) = f (x) - b была бесконечно малой функцией при x → a .

Доказательство этой теоремы проводится по аналогии с доказательством свойства 1 для сходящихся последовательностей

числа 8 и бесконечно малой функции x − 3 при x → 3 , т.е. выполнено

244

равенство 5 + x = 8 + (x − 3) . Следовательно, согласно теореме 1, полу-

требовалось доказать. □ Для разности функций доказательство аналогично.

Следствие 1. Функция может иметь только один предел в точке

то есть A = B . □

Свойство 2. Предел произведения двух функций равен произ-

Свойство 3. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:

245

Доказательства свойств 2,3 аналогичны доказательству свойства 1. Упражнение 1. Доказать свойства 2 и 3.

Пример 2. Найти lim x3 -1 .

x→1 x -1

Решение. Очевидно, что lim (x -1) = 0 . Поэтому свойство 3

x→1

о пределе частного здесь применить нельзя. Однако и limx→1(x3 -1)= 0 .

20. Признаки существования пределов. Не всякая функция, даже ограниченная, имеет предел в точке x = a (при x → ±∞ ). Например, функция y = sin x при x → ∞ предела не имеет.

Теорема 1 (о пределе промежуточной функции). Если функция

f(x) заключена между двумя функциями ϕ (x) и g (x) , стремящимися

кодному и тому же пределу в точке x = a , то есть, если

ε > 0 существуют две окрестности δ1 и δ2 точки а, в одной из которых

выполняется неравенство

246

С учетом неравенств (3) и (4) из неравенства (5) следует нера-

венство -ε < f (x) - A < ε , т. е. lim f (x) = A . □

x→a

Теорема 2 (о пределе монотонной функции). Если функция f (x) монотонна и ограничена при x < a (или при x > a ), то сущест-

вует ее левый предел lim f (x) = f (a - 0) (или ее правый предел

x→a−0

lim f (x) = f (a + 0) ).

x→a+0

Упражнение 2. Доказать теорему 2.

§ 8. Два замечательных предела

называемое первым замечательным пределом.

Докажем равенство (1). Здесь имеем неопределенность вида 00 .

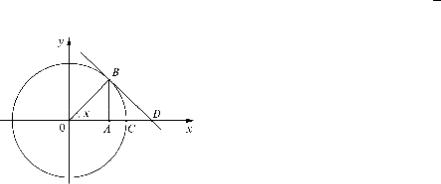
Построим окружность радиуса r =1, возьмем центральный угол с ра-

247

В силу четности входящих функций, эти неравенства справедливы

§ 9. Непрерывность функции в точке

Пусть функция f (x) определена в некоторой окрестности точки x = a . Функция f (x) называется непрерывной в точке а, если

248

Равенство (1) означает выполнение трех условий:

1)функция f (x) определена в точке x = a и в некоторой ее ок- рестности;

2)функция f (x) имеет предел при x → a ;

3)предел функции f (x) в точке а равен значению функции в этой

точке.

Это означает, что при нахождении предела непрерывной функ- ции f (x) можно перейти к пределу под знаком функции, т.е. в функцию

f (x) вместо аргумента x подставить его предельное значение.

равносильны, то получим, что условие непрерывности функции f (x)

249

Согласно определению (3), функция y = sin x непрерывна в любой точке x , x . □

§ 10. Свойства функций, непрерывных в точке

10. Основные свойства функций, непрерывных в точке, непо- средственно следуют из соответствующих свойств их пределов (§7).

Свойство 1. Пусть функции f (x) и g(x) непрерывны в точке

x= a . Тогда функции f (x) ± g(x), f (x) ´ g(x), gf ((xx)) также непрерывны

вэтой точке (последняя при условии, что g (a) ¹ 0 ).

= ( f (x) + g (x)) x=a .□

Аналогично доказываются остальные утверждения.

250

20. Непрерывность элементарных функций. Как известно

(п.4.40), элементарной называется такая функция, которую можно за- дать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операция взятия функции от функции) основных элементарных функций. Поэтому из приведенных свойств о пределах и непрерывности функций вытекает, что всякая элементар- ная функция непрерывна в каждой точке, в которой она определена.

Этот результат позволяет легко находить пределы элементарных функций в точках, где они определены.

§ 11. Точки разрыва функции и их классификация

Точка а называется точкой разрыва функции f (x) , если функция f (x) не является непрерывной в этой точке.

251

Если x = a – точка разрыва функции y = f (x) , то в ней не вы-

полняется, по крайней мере, одно из условий первого определения непрерывности функции, а именно:

1. Функция определена в некоторой окрестности точки а, но не определена в самой точке а.

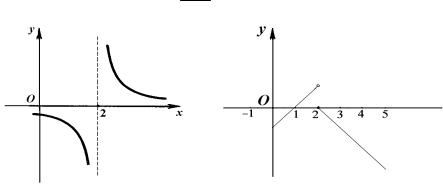
Например, функция y = x -1 2 не определена в точке x = 2 (рис. 1).

(рис. 2), т. к. эта функция не имеет предела в этой точке:

3. Функция определена в точке а и ее окрестности и существует

lim f (x) ¹ f (a).

x→a

252