Математика для инженеров(теория)I том
.pdfПоскольку V является n -мерным, то система векторов e1,e2 ,K,en , x линейно зависима, то есть существуют не все равные нулю числа β1, β2 ,K, βn , βn+1 такие, что
β1e1 + β2e2 +K + βnen + βn+1x = 0 . |
(6) |
Покажем, что βn+1 ¹ 0 . Действительно, предположим противное, то есть βn+1 = 0 , получим, что β1, β2 ,K, βn не все равны нулю, а тогда из (6) следует, что векторы e1,e2 ,K,en линейно зависимы,
что противоречит условию теоремы. Значит, |
|
βn+1 ¹ 0 . |
Сле- |
||||||||||||||||||||||||||||||||||
довательно, из (6) вытекает (5), где αi |
|
= - |
|
βi |
,i = |
|
. |
|
|||||||||||||||||||||||||||||
|
|
1,n |
|
||||||||||||||||||||||||||||||||||
|
βn+1 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Докажем единственность разложения (5). Пусть име- |
||||||||||||||||||||||||||||||||||||
ем |
другую |
систему |
чисел |
|
γ1,γ 2 ,K,γ n |
|
такую, |
что |
|||||||||||||||||||||||||||||
x = γ e1 + γ |
2 |
e2 +K + γ |
n |
en . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Тогда, учитывая (5), имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
α e1 |
+α |
2 |
e2 |
+K +α |
n |
en = γ e1 + γ |
2 |
e2 +K + γ |
n |
en |
|
|
|
|
||||||||||||||||||||
|
или |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(α -γ |
|
) e1 + |
(α |
|
|
|
|
) e2 +K + (α |
|
|
|
|
|
|
|
|
) en |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
2 |
-γ |
2 |
n |
-γ |
n |
= 0 . |
|
|
|
(7) |
|||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Так как векторы e1,e2 ,K,en линейно независимы, то из (7) заклю- |
||||||||||||||||||||||||||||||||||||
чаем, что αi -γi |
= 0,i = |
|
, т. е. αi |
= γ i ,i = |
|
.□ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1,n |
1,n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Выражение |
(5) |
называется |
разложением |
|
вектора x |
|||||||||||||||||||||||||||||||
по базису e1,e2 ,K,en , |
а коэффициенты α ,α |
2 |
,K,α |
n |
– |
коорди- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
натами вектора |
x в базисе e1,e2 ,K,en . |
Если вектор |
x |
в не- |
|||||||||||||||||||||||||||||||||
котором базисе имеет координаты α1,α2 ,K,αn , то записы-
вают x = (α1;K;αn ) .
Отметим, что операции над векторами, введенные в
§1, сводятся к операциям над их координатами.
Чтобы это проверить, надо убедиться в том, что име- ют место следующие свойства: а) вектор x является нуле-
вым вектором n -мерного линейного пространства V тогда и только то- гда, когда все его координаты в любом базисе пространст- ва V равны нулю; б) координаты суммы двух векторов в задан- ном базисе пространства V равны сумме соответствующих ко- ординат рассматриваемых векторов в этом же базисе; в) координаты произведения вектора на число равны произ-
173
ведению соответствующих координат на это число; г) два вектора равны тогда и только тогда, когда равны их соот- ветствующие координаты в одном и том же базисе; д) век-
тор x является линейной комбинацией векторов x1,K, xn тогда и только тогда, когда каждая координата вектора x является такой же ли-
нейной комбинацией соответствующих координат этих векторов в одном и том же базисе.
Вычисление ранга системы векторов сводится к вы- числению ранга матрицы, столбцы которой являются ко- ординатами рассматриваемых векторов. Такую матрицу называют матрицей системы векторов в данном базисе. Обратно, если дана мат-
рица размера n ´ m , то ей можно поставить в соответствие сис- тему m векторов n -мерного линейного пространства, со- стоящую из столбцов этой матрицы.
Пример 2. Найти ранг системы векторов:
x1 = (1;2;3;4), x2 = (2;3;4;1), |
|
x3 = (3;4;1;2), x4 = (4;1;2;3). |
|||
Решение. Составим матрицу из координат этих век- |
|||||
торов: |
|
|
|
|
|
æ1 |
2 |
3 |
4ö |
||
ç |
2 |
3 |
4 |
1 |
÷ |
ç |
÷ |
||||
ç |
3 |
4 |
1 |
2 |
÷ |
ç |
4 |
1 |
2 |
3 |
÷ |
è |
ø |
||||
ис помощью прямого хода метода Гаусса приведем
еек виду
æ1 |
2 |
3 |
4 |
ö |
|
|
ç |
0 |
-1 |
-2 |
-7 |
÷ |
|
ç |
÷ |
, |
||||
ç |
0 |
0 |
4 |
-4 |
÷ |
|
ç |
0 |
0 |
0 |
-160 |
÷ |
|
è |
ø |
|
||||
по которому устанавливаем, что ее ранг равен 4 (ее определитель равен 640 ¹ 0), а значит, ранг указанной системы векторов равен 4. По- скольку система содержит четыре вектора, то она линейно независима и образует базис. □
174
|
|
|
Пример 3. |
|
Проверить, что |
трехмерные |
векторы |
||||||||||||||||||||||||||||
|
x1 = (1;2;-1), |
x2 = (3;6;1), x3 = (3;9;3) |
образуют |
базис |
и |
разло- |
|||||||||||||||||||||||||||||
жить по этому базису вектор |
|
x = (2;5;0) . |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так |
|
|
|
|
|
|
как |
|||||||||
|
|
1 |
3 |
3 |
|
=18 + 6 - 27 +18 -18 - 9 = -12 ¹ 0, |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
6 |
9 |
|
то |
указанные |
векто- |
|||||||||||||||||||||||||||
|
|
-1 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ры образуют базис. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Найдем |
|
|
|
|
|
|
|
коэффициенты |
|
|
|
|
разложения |
|||||||||||||||||||
|
x = α x1 |
+α |
2 |
x2 |
+α |
3 |
x3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Подставляя координаты векторов в это равенство, |
||||||||||||||||||||||||||||||||
получим следующую систему уравнений: |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
α + 3α |
2 |
+ 3α |
3 |
= 2, |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í2α1 + 6α2 + 9α3 = 5, |
|
|
|
|
|
(2) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
-α |
+α |
2 |
+ 3α |
3 |
= 0. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Систему (2) решим по правилу Крамера: = −12 , |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
D1 = |
|
2 |
3 |
3 |
|
= 36 + 0 +15 - 0 -18 - 45 = -12 , |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 6 9 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D2 = |
|
1 |
2 |
|
|
3 |
|
= 0,D3 = |
|
1 |
3 |
2 |
|
= -4. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
5 9 |
|
|
2 |
6 5 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
|
|
3 |
|
|
|
|
|
|
|
|
-1 |
1 |
0 |
|
|
|
|
|
Значит, α1 = DD1 = --1212 =1,α2 = DD2 = 0,α3 = DD3 = --124 = 13.
Итак, искомое разложение имеет следующий вид: x =1× x1 + 0x2 + 13 x3. □
Утверждение 4. Система m векторов n –мерного ли-
нейного пространства линейно независима тогда и только тогда, когда ранг матрицы этой системы равен m .
Упражнение 4. Обосновать приведенное выше ут- верждение.
175
Из утверждения 4 вытекает, что система n векторов n -мерного линейного пространства линейно независима в том и только в том случае, когда матрица этой системы векторов я в л я е т с я н е в ы р о ж д е н н о й .
§ 3. Преобразование координат вектора при замене базиса
Координаты вектора (§2) определяются выбором базиса, а значит, координаты одного и того же вектора будут различными в разных базисах.
Формулами преобразования координат называются формулы, которые связывают координаты вектора в разных базисах.
Пусть в n -мерном линейном пространстве V заданы два различных базиса B1 = {e1,e2 ,K,en} и B2 = {e1′,e2′,K,en′} .
Матрицей перехода от базиса B1 к базису B2 называется матрица системы векторов B2 в базисе B1 . Векторы из B2 единственным образом можно разложить по базису B1 :
|
|
ì e1′ = t e1 |
+ t e2 |
+K+ t |
en , |
|
|
||||||
|
|
ï |
|
11 |
21 |
|
|
n1 |
|
|
|
|
|
|
|
|
|
|
+ t22e2 |
+K + tn2en , |
|
|
|||||
|
|
ïe2′ = t12e1 |
|
(1) |
|||||||||
|
|
í |
....................................... , |
|
|
|
|||||||
|
|
ï |
|
|
|
|
|||||||
|
|
ï |
n′ |
|
1 |
+ t2ne |
2 |
+K + tnne |
n |
. |
|
|
|
|
|
îe |
|
= t1ne |
|
|
|
|
|||||
|
Тогда матрица перехода T от базиса B1 |
к базису B2 |
|||||||||||
и |
м |
е |
е |
|
|
т |
|
|
в |
|
и |
д |
: |
|
|
|
|
æ t |
t |
|
K t |
ö |
|
|
|
|
|
|
|
|
|
ç |
11 |
12 |
|
1n |
÷ |
|
|
|
|
|
|
|
T = çt21 |
t22 |
|
K t2n ÷ . |
|
|
|
(2) |
|||
|
|
|
|
ç |
|
tn2 |
|
|
÷ |
|
|
|
|
|
|
|
|
ètn1 |
|
K tnn ø |
|
|
|
|
|||
Так как столбцы матрицы T – координаты системы |
|||
векторов |
B2 |
в базисе B1 , то, |
с учетом их линейной независимости, |
матрица T |
– |
невырождена. |
Поэтому существует матрица |
T −1 , обратная матрице (2), |
которая является матрицей пе- |
||
рехода от базиса B2 к базису B1 . Всякую невырожденную
матрицу порядка n можно рассматривать как матрицу пе- рехода от одного базиса n -мерного линейного пространст- ва к другому базису этого пространства.
Возьмем произвольный вектор x из n -мерного ли- нейного пространства V и рассмотрим его координаты
176
x1, x2 ,K, xn и x1′, x2′,K, xn′ соответственно в базисах B1 и B2 ,
n n
т. е. x = åxiei = åxi¢ei′.
i=1 i=1
Используя (1), получаем
n |
n |
n |
æ |
n |
åxiei = åxi¢ei′ = åxi¢ |
çç |
åt jie j |
||
i=1 |
i=1 |
i=1 |
è j=1 |
|
Сравнивая в левой и правой ты, которые стоят перед вектором
ö |
n æ |
n |
ö |
|
|
÷ |
ç |
¢ |
÷ i |
. |
(3) |
÷ |
= åç |
åxjtij ÷e |
|||
ø |
i=1 è j=1 |
ø |
|
|
|
частях (3) |
коэффициен- |
||||
ei , будет иметь |
|
||||
n |
|
xi = åtij xj¢,i =1,n . |
(4) |
j=1
Формулы (4) выражают старые координаты x1, x2 ,K, xn вектора x
через его новые координаты и называются фо рмулами преобразования координат при переходе от базиса B1 к базису B2
и л и |
в |
в е к т о р н о й |
|
ф о р м е |
||||||||||||||||||||
|
|
x = T x′ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||
Умножим полученное равенство слева на |
|
T −1 , |
полу- |
|||||||||||||||||||||
чим: |
|
x¢ = T −1x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
||||
Равенство (6) определяет преобразование координат при переходе |
||||||||||||||||||||||||
от базиса B2 |
к базису B1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
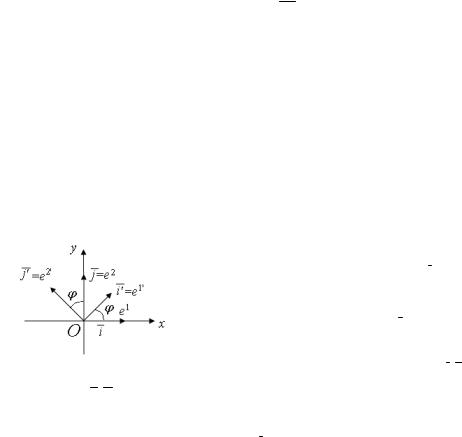
Пример 1. |
Пусть в пространстве |
2 |
||||||||||||||||||||
|
|
заданы базис |
e1 = |
|
,e2 = |
|
|
, |
где |
|
i, |
|
|
|
|
– |
||||||||
|
|
|
|
|
|
j |
|
|
||||||||||||||||
|
|
i |
j |
|
|
|||||||||||||||||||
|
|
|
|
|
1′ |
|
|
2′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
¢ |
|
|||||
|
|
орты, |
и базис |
¢ |
= j |
¢ |
, где |
|
|
|
- |
|||||||||||||
|
|
e |
= i ,e |
|
|
i , j |
|
|||||||||||||||||
|
|
орты, |
причем |
|
|
образует с i угол ϕ |
||||||||||||||||||
|
|
i¢ |
||||||||||||||||||||||
|
|
(рис. 1). Найти |
преобразование ко- |
|||||||||||||||||||||
Рординат при переходе от базиса i, j
ибазису i¢, j¢ .
Решение. Имеем |
|
= cosϕ |
|
+ sinϕ |
|
, |
|
′= -sinϕ |
|
+ cosϕ |
|
. |
||||||||
i¢ |
||||||||||||||||||||
i |
j |
j |
i |
j |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
¢ |
|
¢ |
имеет вид: |
||||||||||||
Матрица перехода T от базиса i, j к базису i , j |
|
|||||||||||||||||||
|
|
æcosϕ |
|
-sinϕ ö |
|
|
|
|
|
|
||||||||||
T = ç |
÷ . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
è sinϕ |
|
|
cosϕ ø |
|
|
|
|
|
|
|||||||||
177

|
|
|
|
|
|
|
|
|
Если вектор |
a |
имеет координаты x, y в базисе i, j и |
||||||
x′, y′ |
|
|
|
– |
||||
в базисе |
|
, |
|
|
x = x′cosϕ - y′sinϕ, y = x′sinϕ + y′cosϕ . |
|||
i¢ |
j¢ , то |
|||||||
Пусть теперь в |
n -мерном линейном пространстве за- |
|||||||
даны три базиса B1,B2 ,B 3= {e1′′,e2′′ ,K,en′′}. Переход от базиса B1 к базису B 3 можно осуществить двумя способами или непосредственно
от B1 к B 3 , или сначала от B1 |
к B 2 , а затем от B 2 |
к B 3 . |
||
Согласно (5) имеют место соотношения: |
x = Tx′, x′ = R x′′, x = Sx′′ , |
|||
где R – матрица перехода от B 2 |
к B 3 ; S |
− матрица перехода |
||
от B1 к |
B 3 . |
|
|
|
Из |
последних |
равенств |
имеем: |
|
x = T x¢ = T (Rx¢¢) = (TR)x¢¢ = Sx¢¢ , отсюда S = TR .
Таким образом, при последовательном преобразовании координат матрица S перехода от базиса B1 к базису B 3 равна про- изведению матриц T и R промежуточных переходов.
§ 4. Евклидово пространство
10. Определение евклидова пространства. В линейном пространстве V кроме операций сложения элементов и умножения элемента на действительное число, введем еще одну опе- рацию – скалярное произведение . Каждой паре векторов
x, y V сопоставим действительное число (x, y) , которое и н а з о в е м с к а л я р н ы м п р о и з в е д е н и е м .
Потребуем, |
чтобы для любых x, y, z V x, y, z V и лю- |
бого числа α |
выполнялись следующие аксиомы: |
1)(x, y) = ( y, x) ;
2)(λx, y) = λ (x, y) ;
3)(x + y, z) = (x, z) + ( y, z) ;
4)(x, x) > 0 при x ¹ 0,(x, x) = 0 для x = 0 .
Очевидно, что скалярное произведение равно нулю, если хотя бы один из векторов нулевой: (0, y) = (0x, y) = 0(x, y) = 0 .
Скалярное произведение (x, x) вектора x на себя называют
скалярным квадратом этого вектора.
178
Евклидовым пространством называется линейное действительное пространство, в котором задана операция скалярного умножения векторов, удовлетворяющая аксио-
мам 1) – 4).
В качестве примера евклидова пространства рассмотрим n-мерное линейное пространство n упорядоченных совокупностей n действитель- ных чисел. Скалярное произведение двух его векторов x = (x1; x2;K; xn ) ,
y = ( y1; y2;K; yn ) , по аналогии со случаями |
n = 2,3 (формула |
(2.7.8)), определим как |
|
(x, y) = x1y1 + x2 y2 +K + xn yn . |
(1) |
Упражнение 1. Проверить, что все аксиомы 1) – 4) скалярного произведения выполняются.
Рассматриваемое линейное пространство со скаляр- ным произведением (1) называется n-мерным евклидовым
пространством n (сохраним для него прежнее обозначе- ние).
20. Норма вектора евклидова пространства. Нормой вектора x
евклидова пространства называется арифметическое зна-
чение корня из скалярного квадрата x2 |
этого вектора: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
= x2 . |
|
||
|
x |
|
|
|
(x, x) |
(2) |
||||
|
|
|
||||||||
Например, в евклидовом пространстве n норма век- тора x = (x1; x2;K; xn ) определяется формулой
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
= x 2 |
+ x |
2 +K + x 2 . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
n |
||
Докажем следующие свойства нормы вектора x . |
|||||||||||||||||||||||||||||||||
1. |
|
|
|
x |
|
|
|
= 0 в том и только в том случае, когда x = 0 . |
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
2. |
|
|
|
α x |
|
|
|
= |
|
α |
|
|
|
|
|
x |
|
|
|
, где α – любое действительное число. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3. (x, y) £ 
 x
x
 ×
× 
 y
y
 .
.
4. 
 x + y
x + y
 £
£ 
 x
x
 +
+ 
 y
y
 .
.
Доказательство. Свойство 1 непосредственно выте-
кает из аксиомы скалярного произведения 4). |
|
||||||||||||||||||||||||||
2 |
. Используя |
аксиомы |
1) |
и |
3), |
получаем |
|||||||||||||||||||||
|
α x |
|
|
|
|
= |
α2 (x, x) |
= |
|
α |
|
|
|
|
|
|
|
|
для любого α . |
|
|||||||
|
|
= |
|
(α x,α x) |
|
x |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
3 |
. По аксиоме 4) имеем |
|
|
x + y |
|
|
|
2 ³ 0 , поэтому |
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
0 £ 
 x +α y
x +α y
 2 = (x +α y, x +α y) = ( y, y)α2 + 2(x, y)α + (x, x) . (3)
2 = (x +α y, x +α y) = ( y, y)α2 + 2(x, y)α + (x, x) . (3)
179