
Математика для инженеров(теория)I том
.pdf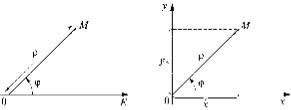
§ 2. Полярная и цилиндрическая системы координат
10 . Полярная система координат. Кроме декартовой системы координат на плоскости широко используется по- лярная система координат. Эта система состоит из точки О, называемой полюсом, и исходящего из нее луча ОЕ, на- зываемого полярной осью. Задается также единица мас- штаба для измерения длин отрезков.
Пусть задана полярная система координат и пусть М
– любая точка плоскости. Обозначим через ρ расстояние от точки М до точки О, а через ϕ − угол, на который нужно повернуть против ча-
совой стрелки полярную ось для совмещения с лучом ОМ
(рис. 1).
Полярными координатами точки М называются числа
ρ и ϕ . Число ρ считают первой координатой и называют полярным радиусом, число ϕ – второй координатой и называют поляр-
ным углом.
Точка М с полярными координатами ρ и ϕ обознача- ется M (ρ;ϕ). Обычно считают, что полярные координаты ρ и ϕ изменяются в пределах: 0 ≤ ρ < +∞, 0 ≤ ϕ < 2π.
Установим связь между полярными координатами точки и ее прямоугольными координатами, считая, что на- чало прямоугольной системы координат находится в по- люсе, а положительная полуось абсцисс совпадает с по- лярной осью. Пусть точка М имеет прямоугольные коор- динаты х и у и полярные координаты ρ и ϕ (рис. 2).
Тогда будем иметь
x = ρ cosϕ, y = ρ sinϕ. |
(1) |
Рис. 1 |
Рис. 2 |
83
Формулы (1) выражают прямоугольные координаты через полярные, а из них полярные координаты через прямоугольные
представляются в виде
|
|
|
y |
. |
|
|
ρ = x2 + y2 , tgϕ = |
(2) |
|||||
|
||||||
|
|
|
x |
|
||
Формула tgϕ = xy определяет два значения полярного угла ϕ ,
т.к. ϕ изменяется в пределах от 0 до 2π.
Если из условий задачи понятно в какой четверти ле- жит точка (x; y), то выбираем тот из полярных углов, ко-
торый соответствует этой четверти. В общем случае для определения угла ϕ пользуются соотношениями
cosϕ = |
|
x |
|
, sinϕ = |
|
y |
|
. |
|
|
|
|
|
|
|
||||
x2 + y2 |
x2 + y2 |
||||||||
|
|
|
|
|
|
|
Пример 1. Даны прямоугольные координаты точки (3; 4). Найти ее полярные координаты, считая, что полюс совмещен с началом прямоугольной системы координат, а полярная ось совпадает с положительной полуосью абс- цисс.
Решение. По формулам (2) имеем |
|
ρ = 5, |
tgϕ = |
4 |
. Согласно |
||||
|
3 |
||||||||
|
|
4 |
|
|
|
4 |
|
||
второму из этих равенств |
ϕ = arctg |
или |
ϕ = π + arctg |
. Но, |
|||||
3 |
|
||||||||
так как x = 3 > 0 и y = 4 > 0 , |
|
|
|
3 |
|
||||
т.е. точка (3; |
4) принадлежит |
||||||||
первой |
|
|
|
|
четверти, |
||||
то ϕ = arctg 43 . □
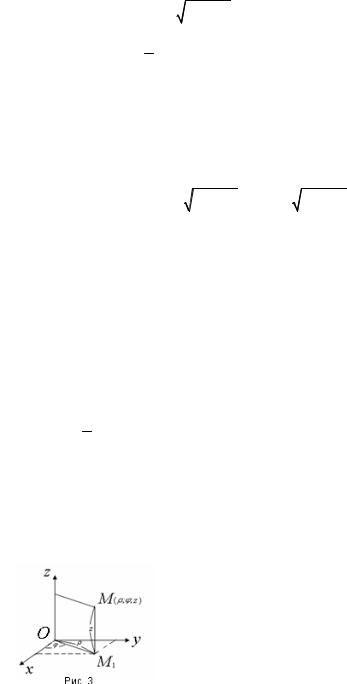
20 . Цилиндрическая система координат. Кроме де-
картовой системы координат в пространстве часто исполь-
зуется цилиндрическая система координат. Здесь произ-
вольная точка М в пространстве однозначно определяется тройкой чисел (ρ;ϕ; z) , где z – аппликата точки М,
z (−∞;+∞) , (ρ;ϕ) – полярные координаты точки M1 , которая является проекцией
точки М на плоскость Оху (рис. 3). Считаем, что полярная ось на плоскости Оху совпадает с положи-
тельным направлением оси Ох при совмещении их начал. Тогда ( см.

р и с . 3 ) легко убедиться , что имеют |
место формулы: |
||
x = ρ cosϕ, |
y = ρ sinϕ, z = z, |
(3) |
|
ρ [0;+∞), |
ϕ [0; 2π ), z (−∞; + ∞) |
|
|
Они выражают декартовы координаты (x; y; z) точки М через ее цилиндрические координаты (ρ; ϕ; z) .
§3. Векторы
Вматематике и ее приложениях различают величины скалярные и векторные. Многие физические величины полностью определяются заданием некоторого числа и на- зываются скалярными. Это, например, площадь, объем, температура тела, масса, работа и т.д. Вместе с тем есть и такие величины, которые определяются не только числом, но и направлением. Например, изучая действие какой-либо силы, нужно указать не только ее значение, но и направ- ление действия этой силы. Такие величины называют вектор-
ными, и для их описания введем понятие вектора.
10 . Понятие вектора. По аналогии со школьным кур-
сом геометрии дадим геометрическое толкование вектора, как направленного отрезка (п. 1.10 ) на плоскости или в пространстве.
Связанным вектором AB с началом в точке А и концом в точке В называют направленный отрезок АВ, в котором точка А является началом, а точка В – концом. Начало вектора на-
зывают еще точкой его приложения.
Векторы также обозначают одной буквой с чертой над ней, например, a . Направление вектора на рисунке указывают стрелкой (рис. 1).
Если для направленного отрезка АВ фиксируютс я только длина и направление (при произвольности его по- ложения на плоскости и в пространстве), то он
a |
B |
н а з ы в а е т с я с в о б о д н ы м в е к т о р о м . |
||||||||||||
A |
|
Длина |
|
AB |
|
|
|
отрезка |
АВ называется |
|||||
|
|
|
||||||||||||
|
также длиной |
|
|
|
|
вектора |
|
|
. Вектор ну- |
|||||
|
|
|
AB |
|
|
AB |
||||||||
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
левой длины называется нулевым и обозна- |
|||||||||||||
|
|
|
|
|||||||||||
чается |
|
или просто 0. |
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
||||
85

Векторы a и b называются коллинеарными (парал- лельными), если они лежат на одной прямой или на парал-
лельных прямых, при этом пишут a || b .
Векторы AB и CD называются одинаково направлен- ными, если полупрямые AB и CD одинаково направлены,
и противоположно направленными, если эти полупрямые п р о т и в о п о л о ж н о н а п р а в л е н ы .
Отметим, что коллинеарные векторы могут быть на- правлены одинаково (сонаправлены, см. рис. 2б)) или про- тивоположно направлены (см. рис. 2а)).
Векторы a и |
|
|
называются равными ( a = |
|
), если |
|||||||||||||
b |
b |
|||||||||||||||||
выполнены два условия: |
||||||||||||||||||
а) |
|
a |
|
= |
|
|
|
|
|
; |
|
|
|
|
|
|||
|
|
|
b |
|
|
|
|
|
|
|||||||||
б) |
|
a и |
|
одинаково направлены. |
||||||||||||||
|
b |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторы, имеющие противо- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
положные направления и равные |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
длины, называются противопо- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложными. Вектор, противопо- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложный вектору a , обозначается |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−a . На рис. 2а) изображены про- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тивоположные, а на рис. 2б) – равные |
||||
Рис. 2 а) |
Рис. 2 б) |
|
|
|||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторы a и b . |
||||
Из определения равенства векторов следует, что ка- |
||||||||||||||||||
ков бы ни был вектор |
a и точка О, всегда можно постро- |
|||||||||||||||||
ить единственный вектор OM с началом в точке О, рав- ный вектору a , или, как говорят, отнести начало вектора a к точке О (см. рис. 3). Такие векторы в аналитической геометрии называют свободными: их можно отнести к общему началу.
Введем еще два понятия, используемые в векторной алгебре. Векторы a, b, c называют компланарными, если суще-
ствует плоскость, которой они все параллельны. Отметим, что нуле- вой вектор коллинеарен любому вектору, и поэтому компланарен с лю- быми двумя векторами.
Пусть в пространстве (или на плоскости) заданы два ненулевых вектора a и b . Отложим их от одной точки О: a = OM , b = ON . В плоскости, проходящей через точки О, M, N, определены два угла между лучами ОМ и ОN, которые
86
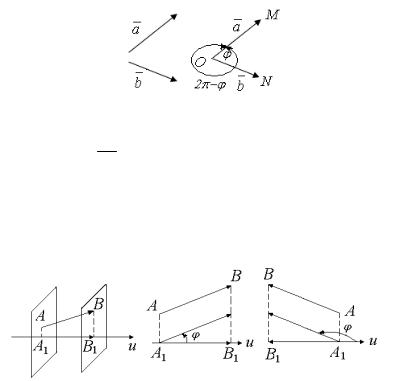
принимают неотрицательные значения |
|
ϕ |
и |
2π −ϕ (рис.3). |
||||||||
Меньший из этих углов (на рис. 3 |
это угол ϕ ) назовем углом |
|||||||||||
|
|
|
|
и обозначим ϕ = |
|
|
|
|
|
|
|
|
между векторами a и b |
|
|
|
|
|
|
|
|||||
(a,b ) . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Очевидно, что |
0 ≤ ϕ ≤ π . Если |
(a,b ) = |
2 |
, то векторы a |
||||||
и |
|
называют ортогональными. |
Нулевой вектор |
|
|
|||||||
b |
0 |
|||||||||||
ортогонален всякому вектору по определению.
Рис. 3
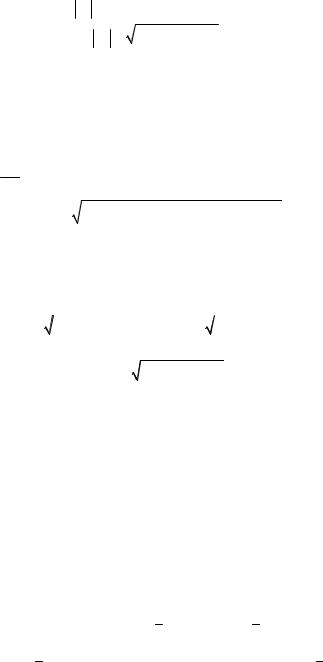
20. Проекция вектора на ось. Пусть в пространстве заданы ось u
и некоторый вектор AB . Проведем через точки А и В плоскости, перпендикулярные данной оси u и обозначим через A1 и
B1 точки пересечения этих плоскостей с осью u (рис.4). В общем
случае векторы расположены на скрещивающихся прямых. Для на- глядности изображений далее, как правило, будут рассматри- в а т ь с я р и с у н к и н а п л о с к о с т и .
Рис. 4 Рис. 5а) Рис. 5б)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проекцией вектора AB на ось |
u |
называется величина |
|||||||||||||||||||||||
A1B1 на оси u , которая обозначается |
|
npu |
AB |
. |
|
|
|
|
|
|
|
|
|||||||||||||
Согласно пункту 1.10 , |
имеем: |
A B = |
|
|
|
|
, |
если |
на- |
||||||||||||||||
|
A B |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
1 |
|
|
|
|
правление |
|
|
совпадает |
с |
направлением |
оси |
u ; |
||||||||||||||||||
A1B1 |
|||||||||||||||||||||||||
A1B1 = − |
|
|
|
|
, |
если |
направление |
|
|
противоположно |
на- |
||||||||||||||
|
A1B1 |
|
A1B1 |
|
|||||||||||||||||||||
правлению оси u . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
87
Покажем, что имеет место равенство
|
|
|
|
|
|
|
|
npu |
AB |
= |
|
|
|
|
AB |
|
cosϕ , |
|
|
|
|
|
|
|
|
(1) |
||||||||||||||||||||||||
где |
|
– угол между вектором |
|
|
|
и положительным |
||||||||||||||||||||||||||||||||||||||||||||
ϕ |
|
AB |
||||||||||||||||||||||||||||||||||||||||||||||||
направлением оси u . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Доказательство. Если ϕ < π |
|
(рис. 5а)), то |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
прu |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
×cosϕ . |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
AB |
A1B1 |
AB |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Если же ϕ > π |
(рис. 5б)), то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
npu |
|
|
= - |
|
|
|
|
|
|
|
|
|
|
|
= - |
|
|
|
|
|
cos(π -ϕ) = |
|
|
|
|
|
cosϕ . |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
AB |
A1B1 |
AB |
AB |
|
||||||||||||||||||||||||||||||||||||||||||||
Таким образом, для любого угла ϕ имеет место ра- |
||||||||||||||||||||||||||||||||||||||||||||||||||
в е |
н |
с |
|
|
т |
|
|
|
в |
|
|
о |
( |
|
|
|
|
1 |
|
|
) |
|
|
|
. |
□ |
||||||||||||||||||||||||
Отметим, |
что если |
|
= |
|
|
и задана ось u , |
то приме- |
|||||||||||||||||||||||||||||||||||||||||||
AB |
CD |
|||||||||||||||||||||||||||||||||||||||||||||||||
няя к каждому из векторов |
AB |
и |
CD |
формулу (1) получаем |
||||||||||||||||||||||||||||||||||||||||||||||
равенство |
npu |
|
= npu |
|
, |
|
т.е. равные векторы имеют рав- |
|||||||||||||||||||||||||||||||||||||||||||
AB |
CD |
|
||||||||||||||||||||||||||||||||||||||||||||||||
ные проекции на одну и ту же ось. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
§ 4. Координаты вектора. Длина вектора. Направляющие косинусы вектора
10. Координаты вектора. Пусть в пространстве задана декартова
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
система координат |
Oxyz и произвольный вектор AB . Обо- |
|||||||||||||||||||
значим: X = npx |
|
, |
|
Y = npy |
|
, |
Z = npz |
|
и |
назовем |
эти |
|||||||||
AB |
AB |
AB |
||||||||||||||||||
числа X , Y, Z |
(проекции вектора |
|
|
на оси координат) |
ко- |
|||||||||||||||
|
AB |
|||||||||||||||||||
ординатами |
вектора |
|
. |
Будем писать |
|
= col(X ; Y; Z) |
||||||||||||||
AB |
AB |
|||||||||||||||||||
(символ col для краткости, |
как правило, далее опускаем). |
|||||||||||||||||||
Докажем, |
что для любых точек A (x1; y1; z1) |
и B (x2; y2; z2 ) |
||||||||||||||||||
координаты вектора |
|
|
определяются формулами: |
|
||||||||||||||||
|
AB |
|
||||||||||||||||||
|
X = x2 - x1, Y = y2 - y1, Z = z2 - z1 . |
|
|
|
|
(1) |
||||||||||||||
88

Доказательство. Проведем через точки А и В плос- кости, перпендикулярные оси O y , и обозначим точки их
|
|
|
|
|
|
пересечения |
с |
этой осью со- |
|||||||||
|
|
|
|
|
|
ответственно через A1 и B1 . |
|||||||||||
|
|
|
|
|
|
Точки |
A1 |
|
и |
B1 |
на оси |
O y имеют |
|||||
|
|
|
|
|
|
координаты |
y1 |
и |
y2 (рис. 1). |
||||||||
|
|
|
|
|
|
|
|
|
По определению координат |
||||||||
|
|
|
|
|
вектора, Y = npy |
|
|
|
= A1B1 . Соглас- |
||||||||
|
|
|
|
AB |
|||||||||||||
|
Рис. 1 |
|
|
|
|
||||||||||||
но п. 1.10 получаем A B = y |
2 |
− y . Аналогично получаем остальные |
|||||||||||||||
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
формулы из (1). □ |
|
|
|
|
|
|
|
|||||||
Отметим, |
что |
если |
|
начало |
вектора |
AB |
совпадает с |
||||||||||
началом координат, т.е. |
|
x1 = y1 = z1 = 0, |
и |
x2 = x, y2 = y , z2 = z, |
|||||||||||||
то координаты |
вектора |
|
|
|
|
равны |
координатам точки В |
||||||||||
|
|
AB |
|||||||||||||||
(конца вектора) X = x , |
Y = y , |
Z = z . |
В случае, если декар- |
||||||||||||||
това система |
координат рассматривается на |
плоскости |
|||||||||||||||
Oxy , то в формулах (1) отсутствует координата Z, то есть
третье равенство.
20 . Длина вектора. Рассмотрим произвольный вектор a = OA = (X ;Y;Z), считая, что его начало совпадает с нача- лом координат O . Пусть вектор a не лежит ни в одной координатной
п |
л |
о |
с |
к |
о |
с |
т |
и |
. |
|
|
|
|
Через |
точку |
А |
проведем |
||
|
|
|
|
плоскости, которые перпенди- |
|||||
|
|
|
|
кулярны осям координат и вме- |
|||||
|
|
|
|
сте с координатными плоско- |
|||||
|
|
|
|
стями |
образуют прямоугольный |
||||
|
|
|
|
параллелепипед, диагональю ко- |
|||||
|
|
|
|
торого будет отрезок |
ОА |
(рис. |
|||
|
|
|
|
2). |
|
|
|
|
|
Известно, что квадрат дли- Рис. 2 ны диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измере-
ний, т.е.
|
|
|
|
|
|
|
|
|
|
OA |
|
2 = |
|
OA |
|
2 + |
|
OA |
|
2 |
+ |
|
OA |
|
2 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
z |
|
|
||||
Но |
|
OA |
|
= |
|
a |
|
, |
|
OAx |
|
= X , |
|
|
|
OAy |
|
= Y, |
|
|
OAz |
|
= Z. |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
89
Тогда имеем a 2 = X 2 + Y 2 + Z 2 или |
|
a = X 2 + Y 2 + Z 2 . |
(2) |
Формула (2) выражает длину вектора через его коор- динаты и справедлива и в том случае, если вектор a будет лежать в какой-либо координатной плоскости (тогда в (2) одна из координат будет равна нулю).
Пример 1. Даны две точки A(x1; y1; z1) и B (x2; y2; z2 ). Найти расстояние между ними.
Решение. Определим расстояние между точками А и В, как длину вектора AB = (x2 − x1; y2 − y1; z2 − z1) :
|
|
|
|
|
|
|
|
d = |
|
AB |
|
= (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2 . □ |
(3) |
||
30. Направляющие косинусы вектора. Обозначим через α, β ,γ
углы между вектором a и осями координат (рис.2). Из формул (3.1) и (2) получаем:
cosα = |
|
X |
|
|
|
, cos β = |
|
|
|
Y |
|
, |
||
|
|
|
|
|
|
|
|
|
|
|||||
X 2 + Y 2 + Z |
2 |
X 2 + Y 2 + Z 2 |
||||||||||||
|
|
|
|
|
|
(4) |
||||||||
|
|
cosγ = |
|
|
|
|
Z |
|
|
|
||||
|
|
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Числа cosα, cos β, cosγ |
|
|
|
|
X 2 + Y 2 + Z 2 |
|
|
|||||||
называются направляющими косинусами |
||||||||||||||
вектора a .
Возводя в квадрат каждое из равенств (4) и складывая полученные результаты, получим
cos2 α + cos2 β + cos2 γ =1, |
(5) |
т.е. сумма квадратов направляющих косинусов любо- го вектора равна единице.
§ 5. Линейные операции над векторами
Линейными операциями над векторами называют операции сложения векторов и умножения вектора на число.
Пусть даны два вектора a и b . Суммой a + b называется вектор, который имеет началом начало вектора a и концом – ко-
нец вектора b при условии, что начало вектора b совпа-
90

дает с концом вектора a (или диагональ параллелограмма,
п о с т р о е н н о г о н а в е к т о р а х a и b ) . Отсюда следует, что сумму неколлинеарных векторов
a и b можно найти по правилу треугольника (рис. 1а)) или параллелограмма (рис. 1б)).
Рис. 1а) Рис. 1б)
По определению суммы двух векторов можно найти сумму любого числа заданных векторов. В частности,
пусть заданы три вектора a,b и c . Сложив a и b , полу- чим вектор a + b. Прибавив к нему вектор c , получим век- тор a + b + c.
Разностью b - a векторов b и a называется вектор c , который в сумме с вектором a дает вектор b .
Пусть даны вектор a ¹ 0 и число α ¹ 0. Произведением α a называют вектор, который коллинеарен вектору a , имеет длину, равную α 
 a , и направление такое же, как и вектор a , если α > 0 , и противоположное, если α < 0 (рис. 2). Если среди сомно- жителей a, α есть 0, то под произведением α a понимается
a , и направление такое же, как и вектор a , если α > 0 , и противоположное, если α < 0 (рис. 2). Если среди сомно- жителей a, α есть 0, то под произведением α a понимается
н у л е в |
|
|
|
|
|
о |
й |
в е |
к |
т |
|
|
|
о |
р . |
||||||
Геометрический смысл операции умножения вектора |
|||||||||||||||||||||
|
на число следующий: если |
|
α |
|
|
>1, то при |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
умножении вектора a на число α век- |
||||||||||||||||||||
|
тор a «растягивается» в |
α |
раз, а |
если |
|||||||||||||||||
|
|
α |
|
|
<1 |
– |
«сжимается» в |
|
1 |
|
раз. На рис. 2 |
||||||||||
|
|
|
|
||||||||||||||||||
Рис. 2 |
|
|
|
α |
|||||||||||||||||
|
α |
|
|
>1. |
|
|
|
|
|
|
|
|
|
|
|
||||||
изображен случай |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Утверждение 1. Если векторы a и |
|
|
коллинеарны и |
||||||||||||||||||
b |
|||||||||||||||||||||
a ¹ 0 , то существует единственное число α , |
что |
|
=α a . |
||||||||||||||||||
b |
|||||||||||||||||||||
Упражнение 1. Доказать сформулированное утвер- ждение 1.
Основные свойства линейных операций.
91

1)a + b = b + a (коммутативность сложения),
2)(a + b ) + c = a + (b + c ) (ассоциативность сложения),
3)α(β a) = (αβ )a, α,β (ассоциативность умножения на
|
число), |
|
|
||||
4) |
(α + β )a = α a + β a, α,β |
(дистрибутивность |
относи- |
||||
|
тельно суммы чисел), |
|
|
||||
5) |
α(a + |
|
) = α a +α |
|
, α Î |
(дистрибутивность |
относи- |
b |
b |
||||||
тельно суммы векторов).
Доказательство. Свойства 1) и 2) вытекают из определения суммы
произвольных векторов a,b ,c с использованием рис. 1а) или 1б). Для доказательства свойства 3) заметим, что векторы α(β a) и
(α β )a имеют одинаковую длину, так как
α(β a) = α 
 β a = α
β a = α 
 β
β 
 a , (α β )a = α β
a , (α β )a = α β 
 a = α
a = α 
 β
β 
 a .
a .
Они также одинаково направлены, поскольку их направление по отношению к направлению вектора a определяется знаком одного
и того же числа α β .
Для доказательства свойства 4) допустим, что ненулевые числа α и β одного знака. Тогда
α a + β a = α a + β a = α 
 a + β
a + β 
 a = = (α + β ) a = α + β
a = = (α + β ) a = α + β 
 a = (α + β ) a ,
a = (α + β ) a ,
а значит, векторы в правой и левой частях равенства 4) имеют одина- ковую длину, и, кроме того, они одинаково направлены.
Пусть теперь α β < 0 и, для определенности, β > α . Отсюда
следует, что числа α + β |
и −α одного знака. Поэтому, в силу дока- |
|||||
занного выше, |
|
|
|
|
|
|
(α + β )a + (-α)a = (α + β -α)a = β a Þ (α + β )a = αa + β a , |
||||||
|
|
|
т.е. получаем дист- |
|||
|
|
|
рибутивность отно- |
|||
|
|
|
сительно суммы |
|||
|
|
|
чисел и в этом слу- |
|||
|
|
|
ч |
а |
е |
. |
|
|
|
|
Д о к а ж е м |
||
|
|
|
свойство 5). Пусть |
|||
|
Рис. 3а) |
Рис. 3б) |
число α > 0. |
Если |
||
|
|
|
||||
92
