Математика для инженеров(теория)I том

Если матрица системы А невырождена (D ¹ 0) , то систему (1)

называют невырожденной. В противном случае ее называют вырож- денной.

Рассмотрим невырожденную систему (1) и запишем ее в мат- ричной форме (6.3). Из теоремы Кронекера-Капелли следует, что решение такой системы существует. Поскольку r(A) = r(A | b) = n . Так

как A ¹ 0 , то матрица А имеет единственную обратную матрицу A−1 .

Умножим матричное равенство Ax = b слева на матрицу A−1 . Получим

равенство

A−1(Ax ) = A−1b.

В силу ассоциативности умножения матриц и соотношения A−1A = E ,

Таким образом, получено решение невырожденной системы (1), записанное в матричной форме (2). Если использовать запись обратной

матрицы A−1 , например, в виде (4.5), то формулу (2) можно записать так:

Таким образом, для невырожденных систем, на основе равенст- ва (3) и определения равных матриц, можно получить решение в виде

Метод обратной матрицы для нахождения решения системы (1) можно преобразовать в метод Крамера, если использовать свойство замены определителя, выраженное формулой (3.12). Тогда получим

A1 jb1 + A2 jb2 + ... + An jbn = D j , j =1,n ,

где D j – определитель, который получается из основного определи-

теля D при замене j-го столбца на столбец свободных членов. Тогда получаем формулы Крамера для нахождения решения системы (1):

Поэтому, если определитель системы (1) не равен нулю, то такая система имеет единственное решение, которое можно найти по фор- мулам Крамера (5).

63

Пример 1. Решить систему ì3x1 - x2 =1,

íî2x1 + x2 = 5.

D2 = 32 15 =15 - 2 =13, x1 = DD1 = 65 , x2 = DD2 = 135 . □

§ 8. Исследование систем линейных уравнений.

Метод Гаусса

10. Исследование систем линейных уравнений. Часто в мате-

матических исследованиях и практических приложениях нужно знать, является ли совместной система (6.1), а если это так, то сколько решений она имеет. Ответ на первую часть поставленного вопроса содержится в теореме Кронекера-Капелли. В частности, невырожденную систему (7.1) можно решить по правилу Крамера и, значит, такая система имеет единственное решение.

В общем случае при исследовании совместной системы используют сформулированные ниже утверждения.

Утверждение 1. Если ранг матрицы совместной системы равен количеству неизвестных, то система имеет единственное решение.

Доказательство. Пусть указанная система совместна. Тогда на основании теоремы 6.1 rank (A) = rank (A b) = n. Поэтому существует

минор, который будет базисным одновременно для матриц А и (A b) . Каждый небазисный столбец матрицы ( A b ) есть линейная комбинация

ее n базисных столбцов. Поэтому система (6.1) эквивалентна системе тех n уравнений первоначальной системы, в которых коэффициенты при неизвестных образуют базисный минор. Последняя система явля- ется невырожденной системой n уравнений с n неизвестными и имеет единственное решение, которое можно найти по правилу Крамера. □

Утверждение 2. Если ранг матрицы совместной системы меньше количества неизвестных, то система имеет бесчисленное множество решений.

Доказательство. В силу теоремы 6.1 r(A) = r (A b) = r , причем

r < n . Изменяя нумерацию неизвестных и переставляя уравнения сис- темы (6.1), можно всегда добиться, чтобы элементы базисного минора

64

М матриц А и (A b) были расположены в левом верхнем углу, что и

Так как каждый небазисный столбец матрицы (A b) есть линей-

ная комбинация базисных столбцов, то исходная система (6.1) будет эквивалентна системе r уравнений с n неизвестными:

Систему (1) запишем так, чтобы в левой части каждого урав- нения были только первые r неизвестных. Придавая неизвестным

xi , i = r +1, n , произвольные числовые значения αr+1, αr+2 , ..., αr+n ,

При произвольных фиксированных αr+1, αr+2 , ..., αn система (2)

и исходной системы (6.1). Поскольку числа αr+1, ..., αn – произволь-

ные, то получаем, что система (6.1) имеет бесчисленное множество решений. □

20. Метод Гаусса. Распространенным точным методом решения систем (1) является метод Гаусса. Суть метода состоит в том, что посредством элементарных преобразований система (1) приводится к треугольной или трапециевидной форме, из которой все решения системы получаются непосредственно.

65

Рассмотрим систему (6.1), где коэффициент a11 ¹ 0 . Если бы было a11 = 0 , то на первое место в системе (1) поставили бы уравнение, в котором коэффициент при x1 отличен от нуля. Пусть далее в i-ом

и сложим его с i-ым уравнением. В результате получим уравнение

(ai1a11 - a11ai1 )x1 + (ai2a11 - a12ai1 )x2 + (ai3a11 - a13ai1 )x3 + ... +

+(aina11 - a1nai1 )xn = a11bi - ai1b1 ,

где коэффициент при x1 равен нулю.

Преобразуем таким образом все уравнения системы, в которых ai1 ¹ 0 (i = 2,n) и, преобразуя соответствующие коэффициенты, получим

систему

в которой рамкой выделена так называемая остаточная часть системы.

Преобразование системы (6.1) в систему (3) выполнено с помощью ее первого уравнения, называемого разрешающим на данном шаге. Исключалась переменная x1 , называемая разрешающей, коэффициент

a11 при ней также называется разрешающим, столбец коэффициентов

Если этого не произойдет, то, предполагая, что a22′ ¹ 0 , из всех уравнений остаточной части системы (3), кроме первого, исключим, аналогично предыдущему, неизвестную x2 .

Продолжая процесс преобразования остаточных частей полу- чающихся систем, придем к одному из двух случаев:

66

1)либо в ходе преобразований получаем уравнение вида 0 × xk + 0 × xk+1 + ... + 0 × xn = b , где b ¹ 0 , и тогда система (6.1) несовместна;

2)либо приходим к системе без остаточной части:

уравнений по сравнению с исходной системой ( r ≤ m ). Это связано с тем, что в процессе преобразований вычеркиваются уравнения вида

0× xj + 0 × xj+1 + ... + 0× xn = 0 .

Процесс преобразования системы (1) к системе (4) называют

прямым ходом метода Гаусса.

Если в системе (4) r = n , то она имеет треугольный вид. Из послед- него уравнения bnn xn = cn находим xn , из предпоследнего – xn−1 и т.д. и, наконец, из первого – x1 , и, тем самым, – единственное решение сис-

темы (6.1). Описанный процесс называют обратным ходом метода Гаусса.

Если r < n , то в результате обратного хода, r неизвестных можно выразить линейно через остальные (n − r) неизвестных. Эти r неиз-

Ясно, что это решение можно записать относительно и других бази- сов, которых может быть не больше Cnr (число сочетаний из п по r).

Чтобы получить какое-нибудь частное решение системы (6.1), нужно придать свободным неизвестным некоторые числовые значения. Ясно, что в случае r < п система (6.1) имеет бесконечное множество решений.

67

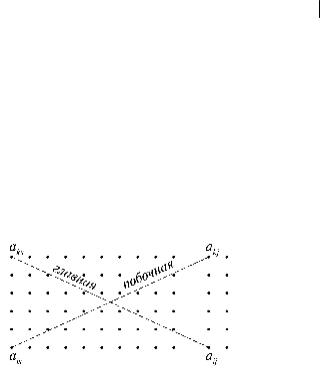
Замечание 1. На практике элементарным преобразованиям подвергают не систему уравнений, а ее расширенную матрицу (A b) .

Применительно к матричной записи процедура гауссовских исключений формализуется следующим образом. Первый шаг (исключение неиз- вестной x1 ) прямого хода выполняется с разрешающим элементом

a11 , второй шаг (исключение x2 ) – с элементом a22′ и т.д., c разре-

шающими диагональными элементами матрицы. Пересчет элементов матрицы выполняется по следующим правилам: 1) элементы разрешаю- щей строки и всех вышерасположенных строк остаются неизменными; 2) элементы разрешающего столбца, расположенные ниже разрешаю- щего элемента, обращаются в нули; 3) все прочие элементы матрицы вычисляются по правилу прямоугольника, согласно которому преоб-

разованный элемент равен разности произведений элементов главной и побочной диагоналей (рис. 1).

Рис. 1

68

единственное решение данной системы. □

30. Нахождение базисных решений системы линейных уравнений. Совместная система линейных алгебраических уравнений называется неопределенной, если она имеет более одного решения. Важную роль в приложениях, в частности в линейном программиро- вании, играют базисные решения такой системы уравнений. Запишем общее решение системы (6.1) в виде (5).

Базисное решение получается из решения (5), если свободным неизвестным придать нулевые значения, т.е. положить xr+1 = xr+2 = ... = xn = 0 . Тогда базисные неизвестные будут равны со-

ответствующим свободным членам, т.е. x1 = c10 , x2 = c20 , ..., xr = cr 0 . Полученное базисное решение (c10; c20; ...; cr0; 0; ...; 0) соответствует базису (x1; ...; xr ) . Если общее решение записать в другом базисе, то получим другое базисное решение. Поскольку из системы n неизвестных можно образовать не больше, чем Cnr базисов, то базисных решений у системы (6.1) может быть не более Cnr .

Пример 2. Найти все базисные решения системы

ìx1 + 3x2 =14,

ïí2x1 - 3x3 = 7, ïî2x2 + x3 = 7.

Решение. В результате прямого хода расширенная матрица

данной системы приводится к виду

69

которому соответствует система двух уравнений с тремя неизвестными. Так что, в общем решении системы две базисные неизвестные выра- жаются через одну свободную. Возможные свободные неизвестные x1, x2 или x3 .

Пусть x1 = 0 . Тогда матрица (6) приобретает вид

§ 9. Решение однородных систем линейных уравнений

Однородная система уравнений

70

есть частный случай системы (6.1). Легко видеть, что система (1) всегда имеет нулевое решение x1 = x2 = ... = xn = 0 , и поэтому она совместна.

Как следует из утверждения 8.1, нулевое решение является единст- венным тогда, когда ранг матрицы системы равен количеству неиз- вестных n. В частности, это справедливо для невырожденной системы n уравнений с n неизвестными. Если ранг матрицы А системы (1) меньше n, то, согласно утверждению 8.2, однородная система (1) будет иметь ненулевые решения. Например, однородная система n линейных уравнений с n неизвестными имеет ненулевые решения в том случае, если она вырождена.

Пусть

λ1, λ2 , ..., λk – некоторые числа, называется линейной комбинацией решений c1, c2 , ...,сk .

Утверждение 1. Любая линейная комбинация решений однород- ной системы линейных уравнений есть также решение этой системы.

Доказательство утверждения 1 получается непосредственной подстановкой линейной комбинации в систему (1). □

сk = (с1k ; с2k ; ..; сnk ) однородной системы называют линейно зависи- мыми, если столбцы матрицы

71

линейно зависимые. В противном случае решения называют линейно независимыми.

Естественно, требуется выяснить, существуют ли в бесконечном множестве решений системы (1) линейно независимые решения.

Утверждение 2. Пусть ранг r матрицы А однородной системы (1) меньше количества неизвестных n. Тогда существует (n - r) линейно

независимых решений x1, x2 , ..., xn−r этой системы, причем каждое

ее решение есть линейная комбинация решений x1, x2 , ..., xn−r .

Доказательство. Считаем для определенности, что базисный минор r-го порядка М расположен в левом верхнем углу матрицы А системы (1), и запишем ее общее решение, используя формулу (8.5):

x1 = с1r+1 xr+1 + ... + с1n xn ,

xr = сrr+1 xr+1 + ... + сrn xn ,

где сij (i =1,r, j = r +1,n) – заданные числовые коэффициенты.

Придадим последовательно свободным переменным следующие n – r совокупностей значений:

……………………………… ;

n–r) xr+1 = 0, xr+2 = 0,K, xn =1 .

Исходя из формулы (3), для всех таких наборов значений построим следующие (n – r) решений:

x1 = (с1 r+1; с2 r+1;K; сr r+1; 1; 0;K; 0);

Решения (4) линейно независимы, т. к. матрица вида (2) для решений (4) имеет ненулевой минор порядка n − r , состоящий из ее последних (n − r) столбцов.

72