Математика для инженеров(теория)I том

Произвольное решение системы (1) получаем, если придадим

Из доказательства утверждения 2 непосредственно вытекает, что максимальное количество линейно независимых решений одно- родной системы равно n – r, где n – количество неизвестных, а r – ранг матрицы системы.

Совокупность максимального количества линейно независимых решений однородной системы (1) называют фундаментальной системой решений.

Ясно, что совокупность (4) является фундаментальной системой решений для (1).

С учетом (3), получаем следующий результат: любое решение

однородной системы линейных уравнений есть линейная комбинация решений фундаментальной системы.

На практике, при решении однородных систем линейных урав- нений в качестве значений свободных неизвестных выбирают, как правило, значения по столбцам единичной матрицы, т.к. это наиболее простой способ вычислений. Тогда получаем систему решений (4),

которую называют нормированной фундаментальной системой решений.

В этом случае общее решение данной системы однородных уравнений можно записать в виде (6).

Рассмотрим теперь неоднородную систему (6.1). Однородную систему (1) назовем соответствующей для неоднородной системы,

если она получается из системы (6.1) заменой свободных слагаемых

b1, b2 , K, bn нулями.

Рассмотрим совместную неоднородную систему (6.1), в которой r < n, где r – ранг ее матрицы А; n – количество неизвестных. В этом случае система (6.1) и соответствующая ей однородная система (1)

73

являются неопределенными. Выясним связь между решениями неод- нородной и соответствующей ей однородной системы.

Теорема 1. Каждое решение неопределенной неоднородной сис-

темы линейных уравнений есть сумма заданного частного решения этой системы и общего решения соответствующей ей однородной системы.

Доказательство. Пусть x = col(x1 ,K, xn ) – заданное частное

решение системы (6.1), а c = col(x10; x20 , K; xr0; α1;K;αn−r ) – общее

решение соответствующей ей однородной системы (1). Используем матричную запись систем (6.1) и (1).

Вектор-столбец x удовлетворяет уравнению Ax = b , а вектор- столбец с – уравнению Ax = 0 .

Имеем:

A (x + c) = Ax + Ac = b + 0 = b .

Таким образом, сумма решений x + c – решение неоднородной системы (6.1).

Пусть теперь вектор-столбец х – произвольное решение системы

(6.1). Тогда

0 = b - b = Ax - Ax = A(x - x ).

Отсюда заключаем, что x - x есть решение однородной систе- мы (1), т. е. x - x = c или x = x + c . □

Из теоремы 1 и формулы (6) получаем, что общее решение неопределенной неоднородной системы (6.1) можно задать формулой

x = x +α1x1 +α2 x2 +K +αn−r xn−r ,

где x1, K, xn−r – фундаментальная нормированная система решений

соответствующей однородной системы; α1, α2 , K,αn−r Î ; x – любое частное решение системы (6.1).

Задания для самостоятельной работы

1.Найти сумму матриц

74

8.Пользуясь свойствами определителей, вычислить следующие опре- делители:

75

14.Пользуясь формулой Крамера, решить следующие системы урав- нений:

15.Методом обратной матрицы решить следующие системы уравне- ний:

76

77

Если точки А и В направленного отрезка AB совпадают, то

величина направленного отрезка AB равна нулю, а на- правление не определено. В дальнейшем направленные от- резки оси будем называть просто отрезками, опуская сло- во «направленный».

Основное тождество. Для любых трех точек А, В и С на оси величина отрезка AC равна сумме величин отрез-

Для установления равенства (1) нужно рассмотреть все возможные случаи расположения точек А, В и С на оси.

Упражнение 1. Проверить равенство (1).

20. Прямоугольная система координат на плоскости. Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую единицу масштаба (рис. 3), обра- зуют прямоугольную (или декартову) систему координат на плоскости.

Ось Ох называется осью абсцисс, ось Оу – осью ординат.

Точка О пересечения осей называется началом координат. Плоскость, в которой расположены оси Ох и Оу, называет-

ся координатной плоскостью и обозначается Оху.

Пусть М – произвольная точка плоскости. Опустим из нее перпен- дикуляры МА и МВ соответственно на оси Ох и Оу. Прямо-

угольными координатами х и у точки М будем называть

79

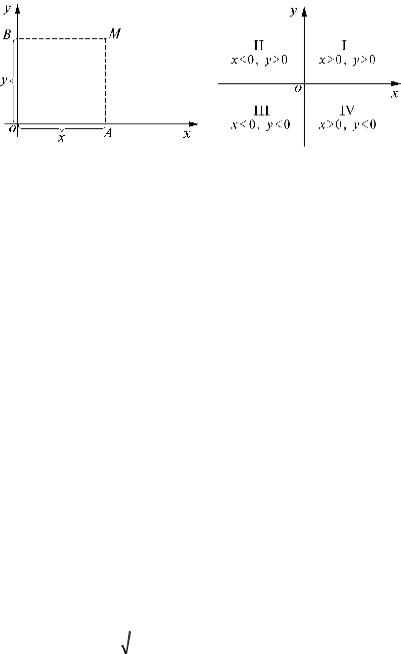
соответственно величины ОА и ОВ направленных отрезков

OA и OB : x = OA, y = OB.

Рис. 3 Рис. 4

Координаты х и у точки М называются, соответствен-

но, ее абсциссой и ординатой.

Тот факт, что точка М имеет координаты х и у, сим- волически обозначают М(х; у). При этом первой в скобках указы- вают абсциссу, а второй – ординату. Начало координат О и м е е т к о о р д и н а т ы ( 0 ; 0 ) .

Таким образом, при выбранной системе координат каждой точке М плоскости соответствует пара чисел (х; у) – ее прямо- угольные координаты и, обратно, каждой паре чисел (х; у) соответствует, и при этом только одна, точка М на плос- кости Оху такая, что ее абсцисса равна х, а ордината у. Значит, прямоугольная система координат на плоскости

устанавливает взаимно однозначное соответствие между множеством всех точек плоскости и множеством упорядо- ченных пар чисел, которое дает возможность при решении геометрических задач применять алгебраические методы.

Оси координат разбивают плоскость на четыре части, их называют

четвертями, квадрантами или координатными углами и нумеруют римскими цифрами I, II, III, IV так, как показано на рис. 4. На рис. 4 также указаны знаки координат точек в зависимости от их расположения в той или иной четверти.

Рассмотрим задачу определения расстояния между двумя точками. Покажем, что для любых двух точек M1(x1; y1) и M2 (x2; y2 ) плоскости расстояние d между ними выражает-

ся формулой

80

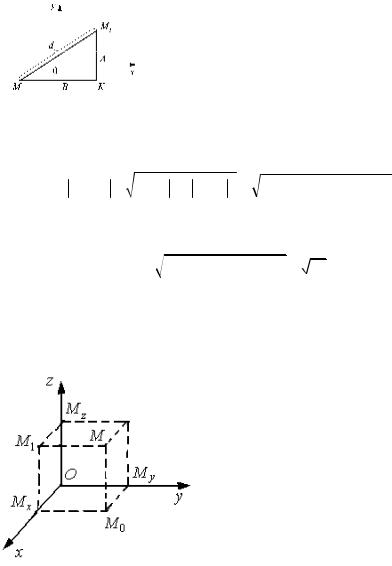
Для доказательства формулы (2) опустим из точек M1

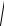
d = M1M2 = M1K 2 + M2K 2 = 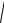(x2 − x1)2 + ( y2 − y1)2 . □

Пример 1. Найти расстояние между точками M1(−1;2) и M2 (4;3) . Решение. По формуле (2) находим

d = 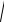(4 − (−1))2 + (3 − 2)2 = 26 . □

30. Декартова система координат в пространстве. Такая система координат Охуz определяется заданием масштабной единицы измерения

длин и трех пересекающихся в одной точке взаимно перпендикулярных осей: Ох, Оу, Оz. Точка О – начало координат, Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат.

абсциссой, у – ординатой, а z – аппликатой точки М.

При выбранной системе координат каждой точке М пространства соответствует единственная упорядоченная тройка чисел (х; у; z) (здесь х означает первое число, у – второе, z – третье) – ее декартовы координаты и, обратно,

81

каждой упорядоченной тройке чисел (х; у; z) соответству- ет, и притом одна, точка М в пространстве.

Таким образом, декартова система координат в про- странстве устанавливает взаимно однозначное соответст- вие между множеством всех точек пространства и множе- с т в о м у п о р я д о ч е н н ы х т р о е к ч и с е л .

Плоскости Оху, Оуz, Охz назовем координатными плоскостями. Они делят все пространство на восемь час- тей, называемых октантами.

40 . Параллельный перенос и его свойства. Напом-

ним, известное из школьного курса геометрии, понятие

называется параллельным переносом.

Название «параллельный перенос» можно объяснить тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

Свойства параллельного переноса:

1)при параллельном переносе прямая переходит в параллельную прямую (или в себя);

2)каковы бы ни были две точки A и A′ существует и притом единственный параллельный перенос, при котором точка A

переходит в точку A′ .

Пусть на прямой задана точка А. Полупрямая или луч − это часть прямой, которая состоит из всех ее точек, ле- жащих по одну сторону от данной точки А, называемой начальной точкой полупрямой. Различные полупрямые од- ной прямой с общей начальной точкой А называются до-

полнительными.

Две полупрямые называют одинаково направленными, если суще- ствует параллельный перенос, который переводит одну полупря- мую в другую.

Две полупрямые называются противоположно на- правленными, если каждая из них одинаково направлена с полупрямой, дополнительной к другой.

82