Математика для инженеров(теория)I том

Доказательство. Докажем вначале первую часть утверждения. Если прямая не перпендикулярна оси Ox , то, как было показано в п.1, она определяется уравнением первой степени y = kx + b , т.е. уравнением

вида (5), где A = k, B = −1 и C = b . Если прямая перпендикулярна

оси Ox , то все ее точки имеют одинаковые абсциссы, равные вели- чине a отрезка, отсекаемого прямой на оси

Ox (рис.2).

Уравнение такой прямой имеет вид x = a , т.е. (5), где A =1, B = 0, C = -a .

Первая часть утверждения доказана. Докажем вторую часть утверждения.

Пусть дано уравнение (5), где хотя бы один Рис. 2 из коэффициентов A или B не равен нулю.

Если B ¹ 0 , то (5) можно записать

оси Ox . □

Линии вида (5) называются линиями первого порядка. Уравне- ние вида Ax + By + C = 0 называется общим уравнением прямой, или

полным уравнением прямой. При различных значениях A, B, C оно определяет всевозможные прямые.

50. Неполные уравнения первой степени. Уравнение прямой в «отрезках». Рассмотрим три частных случая, когда уравнение Ax + By + C = 0 является неполным, т.е. один из коэффициентов равен

нулю:

1) C = 0 ; уравнение имеет вид Ax + By = 0 и определяет прямую,

проходящую через начало координат;

2) B = 0 (A ¹ 0) ; уравнение имеет вид Ax + C = 0 и определяет прямую, параллельную оси Oy . В частности, уравнение x = 0 определяет

ось ординат;

3) A = 0 (B ¹ 0) ; уравнение имеет вид By + C = 0 и определяет прямую, параллельную оси Ox . В частности, уравнение y = 0 определяет ось абсцисс.

123

Рассмотрим теперь уравнение Ax + By + C = 0 при условии, что ни один из коэффициентов A, B, C не равен нулю, т.е. уравнение (5)

Числа a и b является величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения удобна для геометрического построения прямой.

отрезки, величины которых соответственно равны a = −3, b = 2 , и проведем прямую через точки M1(−3; 0) и M2 (0; 2) (рис.3). □

§ 6. Расположение двух прямых на плоскости

10. Угол между двумя прямыми. Рассмотрим две прямые L1 и L2 .

124

Таким образом, один из углов между данными прямыми ра- вен π4 , другой угол π - π4 = 3π4 . □

20. Условие параллельности и перпендикулярности двух прямых на плоскости. Если прямые L1 и L2 параллельны, то ϕ = 0 и

tgϕ = 0 . В этом случае числитель правой части формулы (1) равен нулю, т.е. k2 - k1 = 0 , откуда k2 = k1 .

Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов.

Если прямые L1 и L2 перпендикулярны, т.е. ϕ = π2 , то (из (1)

Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.

Пример 2. Показать, что прямые 2x − 3y +1 = 0 и 6x − 9y + 2 = 0 параллельны.

Решение. Приведя каждое уравнение прямой к виду уравнения с угловым коэффициентом, получаем y = 23 x + 13 и y = 23 x + 92 .

Угловые коэффициенты этих прямых равны: k1 = k2 = 23 . Значит,

прямые параллельны. □

125

30. Взаимное расположение двух прямых на плоскости. Пусть

Пусть A1B2 - A2B1 ¹ 0 . Полученные формулы дают решение

системы (2). Это значит, что прямые L1 и L2 не параллельны и пересе- каются в одной точке с координатами (х; у).

Пусть теперь A1B2 - A2B1 = 0 . Возможны два случая:

1)A2C1 - A1C2 = 0 и B1C2 - B2C1 = 0;

2)A2C1 - A1C2 ¹ 0 ( B1C2 - B2C1 ¹ 0) .

В первом случае имеем A2 = mA1, B2 = mB1, C2 = mC1 , или

A2 = B2 = C2 = m , A1 B1 C1

где m ¹ 0 – некоторое число. Это означает, что коэффициенты уравнений пропорциональны, откуда следует, что второе уравнение получается из первого умножением на число m. В этом случае прямые L1 и L2 сов- падают, т.е. уравнения определяют одну и ту же прямую. Очевидно, что система (2) имеет бесконечно много решений.

Во втором случае, если, например, A2C1 - A1C2 ¹ 0 , то допустив, что система (2) имеет некоторое решение (х0; у0), получим противоречие. Действительно, подставляя в уравнения вместо х и у значения x0 и y0 , умножая первое уравнение на А2, второе – на А1 и вычитая из первого уравнения второе, получим A2C1 - A1C2 = 0 , что противоречит пред-

положению. Таким образом, система (2) решения не имеет. В этом случае прямые L1 и L2 не имеют точек пересечения, т.е. они параллельны.

Итак, две прямые на плоскости либо пересекаются в одной точке, либо совпадают, либо параллельны.

§ 7. Расстояние от точки до прямой на плоскости

10. Нормальное уравнение прямой. Пусть в декартовой системе координат Оху дана прямая L, не проходящая через начало координат. Поместим полярную систему координат так, что полюс О совпадает

126

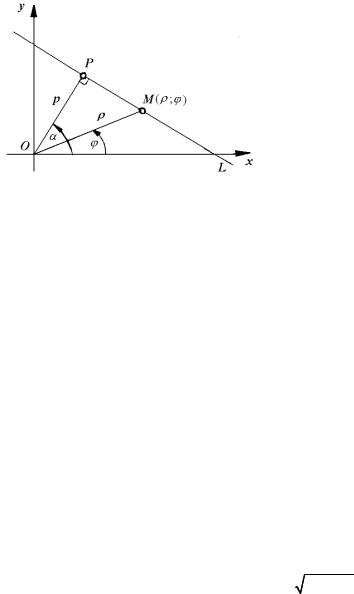
с началом координат декар- товой системы, а полярная ось совпадает с положи-

тельным направлением оси

Ох (рис.1).

Проведем через по- люс О прямую, перпенди- кулярную данной L, и обо-

значим через Р точку ее пересечения с прямой L, а через р длину отрезка ОР. Пусть α – угол между

полярной осью и лучом ОР. Найдем уравнение прямой L, считая известными a и р. Если М(ρ; ϕ) – произвольная точка прямой L, то из

прямоугольного треугольника ОМР имеем

к нормальному виду. Предположим, что А и В не равны нулю одно- временно. Умножим обе части (4) на некоторое число μ ¹ 0 , получим

μ Ax + μBy + μC = 0 . Выберем μ так, чтобы выполнялись равенства

μ выбирается противоположным знаку свободного члена уравнения

(4). Если C = 0 , то для μ можно выбрать любой знак.

Таким образом, общее уравнение прямой (4) приводится к нор- мальному виду умножением на нормирующий множитель μ .

127

Пример 1. Привести уравнение 4x + 3y − 2 = 0 к нормальному виду.

20. Расстояние от точки до прямой. Найдем расстояние d от данной точки M1(x1; y1) до прямой L, заданной нормальным уравне- нием (3) (рис.2). Проведем через точку М1 прямую L1, параллельную L.

Если точка M1(x1; y1) и начало координат О лежат по одну сто- рону от прямой L (рис.3), то, аналогично предыдущему, получим, что

Пример 2. Пусть прямая L задана уравнением 2x − 3y + 5 = 0 и дана точка M (1; 2) . Найти расстояние d от точки М до прямой L.

128

§ 8. Уравнения прямой в пространстве

Рассмотрим различные формы уравнений прямой в пространстве.

10. Общие уравнения прямой в пространстве. Прямая может быть задана пересечением двух плоскостей:

1. Если n1 = (A1; B1;C1) = λ(A2; B2;C2 ) = λn2 т.е. нормальные век-

2. Если n1 ¹ λn2 , т.е. нормальные векторы к плоскостям некол- линеарны, то rA = rB = r = 2 , и система (1) совместна; n − r = 3 − 2 =1,

и плоскости пересекаются, т.е. система уравнений (1) определяет не- которую прямую. Исключив поочередно х и у из системы уравнений

(1) (если это возможно), получим уравнения x = k1z + l1, y = k2 z + l2 .

Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости Oxz и Oyz .

20. Параметрические и канонические уравнения прямой.

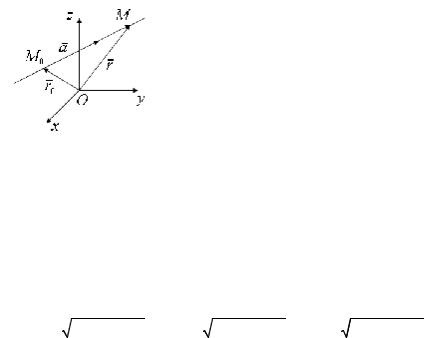
Пусть прямая задана вектором a = (l;m;n) и точкой M0 (x0; y0; z0 ) . На заданной прямой возьмем точку M (x; y; z) (рис.1). Тогда

M0M = r - r0 = λa или в координатной форме

129

Уравнения (3) называют каноническими уравнениями прямой.

В частности, уравнения (3) могут быть записаны в виде

где α, β , γ – углы, образованные прямой с осями координат. Направ- ляющие косинусы прямой находятся по формулам:

130

§9. Угол между прямыми, условия параллельности

иперпендикулярности прямых

Пусть в пространстве две прямые заданы их каноническими уравнениями:

Углом между двумя прямыми считают один из двух смежных углов, которые образуют прямые, проведенные параллельно данным через какую-нибудь точку пространства. Один из этих смежных углов

131

Значит ϕ = π4 , т.е. один из двух смежных углов равен π4 . □

Условие параллельности прямых (1) совпадает с условием кол-

линеарности векторов a1 и a2 . Следовательно, согласно § 2.5, оно

имеет вид

Если при этом точка первой прямой, например, M1(x1; y1; z1)

удовлетворяет уравнению второй прямой, то эти прямые совпадают.

Условие перпендикулярности прямых (1) равносильно условию перпендикулярности их направляющих векторов a1 и a2 , и согласно формуле (2.7.10), запишется так:

Необходимое и достаточное условие расположения двух пря- мых, заданных их каноническими уравнениями, в одной плоскости (ус-

ловие компланарности двух прямых), имеет вид

Если величины l1,m1,n1 не пропорциональны величинам l2 ,m2 ,n2 ,

то условие (5) является необходимым и достаточным условием пере- сечения двух прямых в пространстве.

132