Математика для инженеров(теория)I том

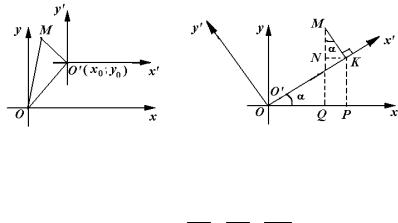
10. Преобразование прямоугольных координат. Рассмотрим три вида преобразований прямоугольных координат на плоскости:

1)параллельный перенос осей координат, когда изменяется положение начала координат, а направления осей остаются прежними;

2)поворот осей координат, когда обе оси поворачиваются на один и тот же угол, а начало координат не изменяется;

3)зеркальное отображение, когда направление одной из коор- динатных осей меняется на противоположное, а направление второй не меняется.

10.1. Параллельный перенос осей координат.

носе старой системы координат в эту точку.

Тогда для любой точки М плоскости, имеющей координаты (х; у)

в системе координат Оху, имеем: OM = OO′ + O′M или в координатной

форме

Формулы (1) устанавливают связь между старыми и новыми ко-

ординатами и определяют параллельный перенос координатных осей.

10.2. Поворот осей координат. Пусть на плоскости задана старая система координат Оху и новая O′x′y′ , полученная в результате

поворота старой системы около точки О на угол α (рис. 2). Тогда для любой точки М плоскости имеем:

OQ = OP − QP = OP − NK ; MQ = MN + NQ = KP + MN.

Отсюда

x = x′cosα − y′sinα ,

(2)

y = x′sinα + y′cosα .

Таким образом, формулы (2) устанавливают связь между ста-

рыми и новыми координатами и определяют поворот координатных осей на угол α .

143

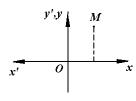
10.3. Зеркальное отображение. Считаем,

что задана старая система координат Oxy и но- вая Ox′y′ , полученная в результате зеркально- го отображения относительно оси Oy (рис. 3).

Тогда для любой точки М плоскости имеем:

Рис. 3 x = -x′, y = y′.

Формулы (3) устанавливают связь между старыми и новыми координатами и определяют зеркальное отображе- ние относительно оси Оу. Аналогичные формулы ( x = x′, y = -y′ )

получаем и при зеркальном отображении относительно оси Ох.

20. Общее уравнение линии второго порядка. Общее уравнение л и н и и в т о р о г о п о р я д к а и м е е т с л е д у ю щ и й в и д :

где A, B, C, D, E, F – любые заданные числа, но A, B и C одновре- менно не равны нулю (A2 + B2 + C2 ¹ 0) .

Утверждение 1. Пусть AC - B2 ¹ 0 . Тогда уравнение (4) с по-

мощью параллельного переноса и поворота осей координат приводится к виду

системе координат.

Доказательство. Осуществим параллельный перенос осей ко- ординат Ох и Оу в точку O′(x0; y0 ) . Тогда старые координаты (x; y)

будут связаны с новыми (x′; y′) формулами (1), а уравнение (4) в новых

координатах примет вид

Это можно сделать единственным образом, т.к. AC - B2 ¹ 0 .

При таком выборе пары чисел x0 , y0 уравнение (6) примет вид

144

Повернем теперь систему координат O′x′y′ на угол α и получим новую систему координат O′x′′y′′ , где старые координаты x′, y′ связаны

C′ = Asin2 α − 2B cosα sinα + C cos2 α.

Выберем угол α так, чтобы коэффициент B′ в уравнении (9) обратился в нуль, что приведет к тригонометрическому уравнению

таком выборе α уравнение (9) примет вид (5). □ Отметим еще, что уравнения (7) называются уравнениями центра

линии второго порядка, а точка (x0; y0 ) называется центром этой

линии. Из §1.8 вытекает, что отличие от нуля числа AC − B2 (опреде- лителя системы (7)) является необходимым и достаточным условием существования единственного решения системы (7).

30. Инвариантность выражения АС – В2. Классификация линий второго порядка.

Утверждение 2. При параллельном переносе и повороте осей координат выражение АС – В2 остается неизменным.

Доказательство. Коэффициенты А,В,С при старших членах уравнения (4) при параллельном переносе осей координат не меняются.

Значит, не меняется и выражение AC − B2 . При повороте осей коор- динат коэффициенты А,В,С заменяются на A′, B′,C′ . Имеем

A¢C¢ - B¢2 =

=(Acos2 α + 2Bcosα sinα + C sin2 α )×(Asin2 α - 2Bcosα sinα + C cos2 α )-

-éë(C - A)cosα sinα + B(cos2 α - sin2 α )ùû2 =

= AC (cos2 α + sin2 α )2 - B2 (cos2 α + sin2 α )2 = AC - B2 ,

что и требовалось показать. □

145

Величину AC − B2 называют инвариантом общего уравнения линии второго порядка, и в зависимости от ее знака, линии второго порядка подразделяются на следующие три типа:

1)эллиптический, если AC − B2 > 0;

2)гиперболический, если AC − B2 < 0 ;

3)параболический, если AC − B2 = 0 . Рассмотрим линии различных типов.

1) Эллиптический тип. Т.к. AC − B2 > 0 , то на основании утверждения 1 общее уравнение (4) приводится к виду (для удобства записи штрихи у коэффициентов и координат опускаем):

а) A > 0, C > 0 (случай A < 0, C < 0 сводится к случаю A > 0, C > 0 умножением уравнения (10) на –1) и F<0. Перепишем уравнение (10)

в эквивалентной форме

x2 + y2 =1, a2 b2

где a2 = − FA , b2 = − CF . Это каноническое уравнение эллипса.

б) A>0, C>0 и F>0. Аналогично предыдущему будем иметь

x2 + y2 = −1. a2 b2

Этому уравнению не удовлетворяют координаты ни одной точки плоскости. Его называют уравнением мнимого эллипса.

в) A > 0, C > 0, F = 0. Уравнение примет вид: a2 x2 + c2 y2 = 0 , где

a2 = A, c2 = C . Ему удовлетворяет только точка О(0;0). Такое уравне- ние называют уравнением пары мнимых пересекающихся прямых.

2) Гиперболический тип. В этом случае AC − B2 < 0 и общее уравнение (4), согласно утверждению 1, также приводится к виду (10).

Возможны следующие случаи:

а) A>0, C<0 (случай A<0, C>0 рассматривать не надо, т.к. умно- жением (10) на –1 он сводится к случаю A>0, C<0) и F ¹ 0 (для опре- деленности считаем, что F<0). Перепишем тогда уравнение (10) в виде

x2 − y2 =1, a2 b2

где a2 = − FA , b2 = CF и получим каноническое уравнение гиперболы.

146

пару пересекающихся в начале координат прямых.

3) Параболический тип. Если AC - B2 = 0 , то поворотом осей координат на угол α, как и при доказательстве утверждения 1, общее уравнение (4) приводится в виду

причем здесь AC = 0 , т.е. один из коэффициентов А или С равен нулю. Пусть A ¹ 0, C = 0 . Представим (11) так:

y′ = y . Получим уравнение

болы с осью симметрии O′′y′′ и вершиной в точке O′′ . б) Е = 0. Уравнение (13) имеет вид

147

ние (14) запишем в виде (x′ − a)(x′ + a) = 0 , которое определяет пару

параллельных прямых.

В случае, когда A и F* одинакового знака, уравнение (14) можно

записать в виде x′2 + a2 = 0 и ему не удовлетворяют координаты ни одной точки плоскости. Оно называется уравнением пары мнимых параллельных прямых.

При F* = 0 уравнение (14) принимает вид x′2 = 0 и определяет ось O′y′ . Это уравнение определяет пару совпадающих прямых.

Обобщив рассмотренные случаи, можно сформулировать полу- ченные результаты в виде теоремы.

Теорема 1. Пусть в прямоугольной системе координат Оху задано общее уравнение линии второго порядка (4). Тогда существует такая прямоугольная система координат, в которой уравнение (4) принима- ет один из следующих девяти простейших (канонических) видов:

1) эллипс x2 + y2 =1; a2 b2

2) мнимый эллипс x2 + y2 = −1; a2 b2

3) пара мнимых пересекающихся прямых a2 x2 + c2 y2 = 0 ;

4) гипербола x2 − y2 =1; a2 b2

5)пара пересекающихся прямых a2 x2 − c2 y2 = 0 ;

6)парабола x2 = 2 py ;

7)пара параллельных прямых x2 − a2 = 0 ;

8)пара мнимых параллельных прямых x2 + a2 = 0 ;

9)пара совпадающих прямых x2 = 0 .

Вэтих формах х и у равноправны, т.е. их можно менять местами.

§15. Уравнение кривых второго порядка

вполярных координатах

148

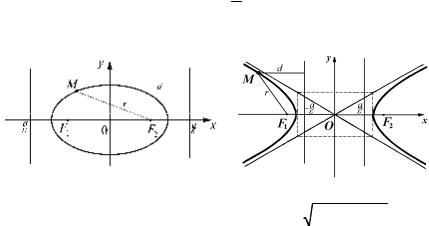
10. Общее свойство директрис эллипса и гиперболы. С помощью понятий директрисы и эксцентриситета (§11, §12) формулируется общее свойство, присущее эллипсу и гиперболе.

Утверждение 1. Отношение расстояния r от произвольной точки эллипса (гиперболы) до фокуса к расстоянию d от этой точки до соот- ветствующей директрисы есть постоянная величина, равная эксцен-

триситету эллипса (гиперболы), т.е. dr = ε .

Доказательство. Рассмотрим для эллипса правый фокус и пра- вую директрису. Пусть М(х; у) – произвольная точка эллипса (рис. 1).

Для гиперболы (рис. 2) рассмотрим левый фокус и левую дирек- трису. Если М(х; у) – произвольная точка левой ветви гиперболы (рис. 2),

Все остальные случаи рассматриваются аналогично. □ Отметим, что доказанное свойство эллипса и гиперболы можно

положить в основу общего определения этих линий: множество точек,

для которых отношение расстояний от фокуса до соответствующей директрисы является величиной постоянной, равной ε , есть эллипс, если ε <1 , и гипербола, если ε >1 .

Как следует из §13, таким же свойством определяется и парабола, если считать ε =1 .

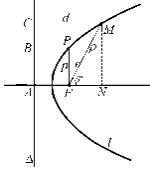
20. Уравнение эллипса, гиперболы, параболы в полярных координатах. Пусть l – дуга эллипса, гиперболы или параболы (рис.3). Если r – расстояние от произвольной точки М этой дуги до фокуса F, d – расстояние от нее до соответствующей директрисы , то из пункта 10 получаем, что

149

d

Проведем через фокус прямую, перпендикулярную директрисе . Пусть А – точка ее пересечения с директрисой, N – проекция точки М на эту прямую. Через точку F проведем перпендикуляр к прямой AN до пересечения с дугой l в точке Р, длину отрезка FP обозначим через р

Уравнение (5) называется полярным уравнением эллипса, пара-

болы, гиперболы. В случае гиперболы это уравнение определяет одну из двух ее ветвей. Отметим, что для параболы параметр р в уравнении

(5) совпадает с ее параметром р из §13, а для эллипса и гиперболы

в полярных координатах?

Решение. Разделив числитель и знаменатель правой части на 5,

150

§ 16. Поверхности второго порядка

Общее уравнение поверхности второго порядка имеет следующий

вид:

F(x, y, z) = Ax2 + By2 + Cz2 + 2Dxy + 2Exz + 2Kyz + 2Gx + 2Ly + 2Mz + N = 0,

где A, B,..., N – любые заданные числа, но A, B, C, D, E, K одновре-

менно не равны нулю (A2 + B2 + C2 + D2 + E2 + K 2 ¹ 0) .

Как и для кривых второго порядка, можно показать, что для каждого уравнения указанного вида легко найти специальную декар- тову систему координат, в которой оно примет наиболее простой, так называемый, канонический вид, позволяющий исследовать форму этой поверхности.

После полного исследования всех возможных канонических уравнений можно убедиться, что существуют различные типы по- верхностей второго порядка, среди которых есть мнимые, а также распадающиеся на пару плоскостей. Ограничимся изучением вещест- венных поверхностей второго порядка.

10. Сфера. Точками сферы являются те, и только те точки пространства, расстояние от которых до заданной точки М равно R. В декартовой системе координат сфера, имеющая центр в точке M(a; b; c) и радиус R, определяется уравнением

Если центр сферы находится в начале координат, то ее уравнение

имеет вид

Пример 1. Найти координаты центра и радиус сферы, заданной уравнением x2 + y2 + z2 - 2x + 2y + z +1 = 0 .

Решение. Приведем уравнение сферы к каноническому виду (1). Для этого дополним до полных квадратов члены, содержащие x, y, z, т.е. перепишем уравнение в виде

(x2 - 2x +1) + ( y2 + 2y +1) + (z2 + z + 14) -1-1- 14 +1 = 0 или (x -1)2 + (y +1)2 + (z + 12)2 = 54 .

151

R = 25 . □

Пример 2. Составить уравнение сферы, проходящей через точки A(1;2;−4) , B(1;−3;1) и С(2;2;3), если ее центр находится в плоскости Оху.

Решение. Так как точки А, В, С принадлежат сфере (x - a)2 + (y - b)2 + (z - c)2 = R2 , центр которой находится в плоскости

Оху, то их координаты должны обращать искомое уравнение в тожде- ство и c = 0 . Поэтому, имеем систему уравнений:

ìï(1- a)2 + (2 - b)2 + (-4)2 = R2 ,

ïí(1- a)2 + (-3 - b)2 +12 = R2 , ïïî(2 - a)2 + (2 - b)2 + 32 = R2.

Отсюда

Таким образом, a = −2, b =1. Следовательно, центр сферы – точка

M (−2;1;0) . Дальше находим R2 = (1- a)2 + (2 -b)2 +16 = 32 +12 +16 = 26 .

Итак, искомое уравнение сферы имеет вид (x + 2)2 + ( y -1)2 + z2 = 26 . □

20. Цилиндрические поверхности. Поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направ- ляющей) и остающейся параллельной некоторому заданному направ- лению, называется цилиндрической.

Уравнение вида F(x, y) = 0 в декартовой системе координат

в пространстве определяет цилиндрическую поверхность, у которой образующие параллельны оси Oz. Аналогично, уравнение F(x, z) = 0

определяет цилиндрическую поверхность с образующими параллель- ными оси Oy, а F(y, z) = 0 – цилиндрическую поверхность с обра-

зующими параллельными оси Ох.

Канонические уравнения цилиндров второго порядка:

эллиптический цилиндр

152