Математика для инженеров(теория)I том

2 0 . З на коо пр еделе нные кв адр ат ич н ые фо рмы .

Квадратичная форма (2) называется положительно определенной, если она приводится к нормальному виду, состоящему из n

Утверждение 1. Квадратичная форма (2) является положительно определенной тогда и только тогда, когда она принимает

положительные значения при любой ненулевой системе значений переменных x1, x2 ,K, xn .

Упражнение 1. Доказать утверждение 1.

Установим критерий положительно определенной квадратичной формы. Главными минорами квадратичной формы (2) называют миноры порядка 1, 2,K,n ее матрицы А, располо-

женные в левом верхнем углу, т.е. числа

Теорема 2 (критерий Сильвестра). Квадратичная форма (2) является положительно определенной тогда и только тогда, когда все ее главные миноры (7) положи- тельны.

Доказательство. Теорему 2 докажем методом мате- матической индукции. При n =1 теорема верна, т. к. квад-

ратичная форма a11x12 – положительно определенная в том и только в том случае, если a11 > 0 . Докажем теорему для

случая n переменных, считая ее справедливой для квадра- тичных форм от n −1 переменных.

Запишем квадратичную форму (2) в виде

переменных x1,K, xn−1 , составленная из тех членов квадратичной формы Q, которые не содержат переменной xn .

203

Очевидно, что главные миноры формы Q1 совпадают с главными

минорами формы Q, кроме последнего.

Пусть квадратичная форма Q является положительно определенной. Покажем, что тогда квадратичная форма Q1 также является положительно определенной. Предполагая противное,

для которой Q(x10 , x20 ,K, xn0 )≤ 0 , что противоречит предпо-

ложению. Значит, по индуктивному допущению, все глав- ные миноры квадратичной формы Q1 , т. е. все главные ми-

норы формы Q, кроме последнего, положительны. Послед- ний главный минор формы Q, т. е. определитель матрицы А, также будет больше нуля. Действительно, квадратич-

ную форму Q(x1, x2 ,K, xn ) можно привести к нормальному

следней формы равен единице, т. е. больше нуля. Поскольку определители матриц конгруэнтных невы-

рожденных квадратичных форм имеют одинаковые знаки, то и A > 0 .

Таким образом, все главные миноры положительно определенной квадратичной формы положительны.

Обратно, пусть все миноры (7) положительны. Тогда, очевидно, положительны также и все главные миноры квадратичной формы Q1 . Форма Q1 по индуктивному до-

пущению – положительно определенная. Значит, найдется такое преобразование переменных x1, x2 ,K, xn , которое приво-

дит форму Q1 к виду Q2 = y12 + y22 +K + yn−12 . Дополним это преоб- разование до невырожденного преобразования всех пере-

менных x1, x2 ,K, xn , положив xn = yn .

С помощью указанного преобразования квадратичную форму Q, в силу (8), приведем к виду

204

где bin ,i =1,n , – некоторые вещественные коэффициен-

невырожденными линейными преобразованиями. Опреде- литель матрицы А этой формы больше нуля. Значит c > 0 . Поэтому квадратичная форма (2) является положительно определенной. □

Квадратичная форма (2) называется отрицательно определенной, если она является невырожденной и приводится к нор- мальному виду, содержащему только отрицательные квад- раты всех переменных.

Положительно определенные и отрицательно определенные квадратичные формы называют знакоопределенными квад- ратичными формами.

Вырожденные квадратичные формы, нормальный вид которых состоит из квадратов переменных одного знака,

называют полуопределенными (соответственно неотрица- т е л ь н ы м и , н е п о л о ж и т е л ь н ы м и ) .

Неопределенными называют квадратичные формы, нормальный вид которых содержит как положительные так и отрица- тельные квадраты переменных.

30 . Приведение квадратичной формы к каноническому виду ортогональным преобразованием. Покажем, что квадратичную форму (2) можно привести к каноническому виду с помощью ортогонального преобразования.

Рассмотрим квадратичную форму двух переменных x1, x2 и найдем оператор Т, диагонализирующий соответствующую ей матрицу

205

Р а с с м о т р и м с о б с т в е н н ы е в е к т о р ы м а т р и ц ы А :

Собственными векторами диагональной матрицы яв- ляются единичные базисные векторы, т. е.

Подобная ситуация имеет место и в случае квадратичной формы n переменных, а именно, приведение квадратичной формы к каноническому

превращается в преобразование TT AT = L и отпадает необходимость

находить обратную матрицу T −1 .

Пример 1. Найти ортогональную матрицу, приводящую квадра-

к каноническому виду, и записать канонический вид квадратичной формы.

Решение. Матрица этой квадратичной формы имеет

вид

206

откуда λ1 = -2,λ2 = λ3 = 7 .

Для нахождения собственных векторов, соответст- вующих значению λ = −2 , получим систему:

Найдем теперь собственные векторы, соответствующие λ2 = λ3 = 7 . Система для нахождения их координат следующая:

ì-x1 + 2x2 + 2x3 = 0,

ïí2x1 - 4x2 - 4x3 = 0,Û x1 - 2x2 - 2x3 = 0. ïî2x1 - 4x2 - 4x3 = 0,

П о л а г а я x3 = c1, x2 = c2 и м е е м x1 = 2c1 + 2c2 . П о л у ч а е м

двупараметрическое семейство собственных векторов (2c1 + 2c2;c2;c1 ) , где c12 + c22 ¹ 0 . Из этого семейства выделим д в а о р т о г о н а л ь н ы х в е к т о р а . П о л о ж и в , н а п р и м е р ,

207

Ей соответствует невырожденное линейное преобразование (14):

применяя которое, получим искомую квадратичную

форму

Q( y1, y2 , y3 ) = λ1 y12 + λ2 y22 + λ3 y32 = -2y12 + 7 y22 + 7y32 . □

§ 12. Применение квадратичных форм к упрощению кривых и поверхностей второго порядка

10. Упрощение уравнений кривых второго порядка. Уравнение кривой второго порядка имеет вид

где коэффициенты a11,a12 ,a13 одновременно в нуль не

обращаются.

Отметим, что в §3.14 изложен геометрический подход к исследованию линий второго порядка, заданных уравне-

208

ниями вида (1). Здесь уравнение (1) будем упрощать, ис- пользуя теорию квадратичных форм двух переменных.

Первые три члена левой части уравнения (1) образу-

Поскольку при ортогональном преобразовании переменных опре- делитель матрицы квадратичной формы не меняется, то

ки. В случае 1) кривая, определяемая уравнением (1), назы-

вается кривой эллиптического типа, а в случае 2) – гипер-

болического типа. Выделив в левой части (6) полные квадраты, получим

209

где

Уравнения (9) выражают параллельный перенос точки пересечения координатных осей в точку O1 (a1;b1 ) .

Если λ1λ2 > 0 , то уравнение (8) приводится к одному

в случае c1 = 0 .

Уравнение (10) определяет эллипс, уравнению (11) не

удовлетворяют координаты ни одной точки плоскости (часто говорят, что это уравнение определяет мнимый эл-

взависимости от знаков λ1 и с1 : (13) в случае λ1с1 > 0 ;

(14)при λ1c1 < 0 ; (15), если c1 = 0 .

Отметим, что уравнение (13) определяет гиперболу с действительной осью O1x′′ , уравнение (14) – гиперболу с

действительной осью O1y′′ , уравнение (15) – пару пересе-

кающихся прямых

210

(оба в нуль обращаться не могут, т.к. квадратичная форма

(2) является невырожденной). Дальше, для определенно-

ние (18) в одном из видов:

в зависимости от знаков λ1 и с1 : λ1c1 < 0 , λ1c1 > 0 , c1 = 0 . Уравнение (19) определяет пару параллельных пря-

мых x′′ = a , x′′ = -a ; уравнению (20) не удовлетворяют координаты ни одной точки плоскости (уравнение (20) определяет пару мнимых параллельных прямых); уравнение (21) определяет пару совпадающих

отнесением кривой к главным осям. Новые оси координат параллельны осям симметрии кривой. Главными направлениями кривой, заданной уравнением (1), будут направления ортогональных собственных векто- ров матрицы квадратичной формы, соответствующей этому уравнению.

211

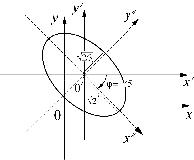
Отметим, что иногда при приведении уравнения (1) к канониче- скому виду удобно вначале сделать параллельный перенос, а затем поворот координатных осей, т. е. отнести кривую к главным осям.

Пример 1. Найти каноническое уравнение кривой

212