Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика для инженеров(теория)I том

.pdf

Скачиваний:

103

Добавлен:

18.02.2016

Размер:

4.09 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 6014 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

через z : x = 2z, y = −3z . Подставляя x и y в равенство

x +1

y + 5

2z +1

-3z + 5

имеем

, откуда

z =1.

Значит x = 2, y = −3 . Искомая

□

точка пересечения M0 (2;-3;1) .

Пример 3. Найти расстояние между скрещивающимися прямыми

y -1

z + 2

(6)

-2

x +1

y +1

z - 2

(7)

-1

Решение. Найдем уравнение плоскости, проходящей через прямую, заданную уравнениями (6), параллельно прямой, заданной уравнения- ми (7). Точка A(0;1; − 2) лежит на прямой (6) и, следовательно, при-

надлежит искомой плоскости. В качестве нормального вектора к этой плоскости возьмем вектор n, определенный через векторное произве- дение неколлинеарных направляющих векторов прямых (6) и (7)

n =

-2 0 1

= -2

- 4

-1

Уравнение искомой плоскости: −2x − (y −1) − 4(z + 2) = 0, или, в

общем виде,

2x + y + 4z + 7 = 0.

(8)

Расстояние между заданными прямыми равно расстоянию любой

точки прямой (7), например,

точки B(−1; −1; 2)

до плоскости (8).

Тогда искомое расстояние

d =

2 ×(-1) +1×(-1) + 4 × 2 + 7

. □

22 +1+ 42

§ 10. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости

Пусть дана прямая, заданная каноническими уравнениями

x - x0	=	y - y0	=	z - z0
l		m		n

и плоскость

Ax + By + Cz + D = 0 .

(1)

(2)

133

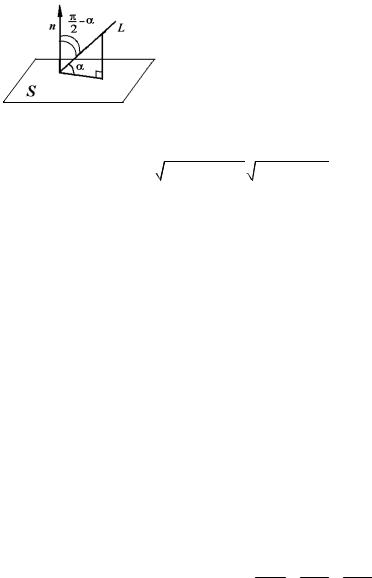
Углом между прямой L и плоскостью S считают острый угол

αмежду этой прямой и ее проекцией на плоскость S (рис.1).

Вданном случае направляющий вектор прямой (1) a = (l;m;n) , а нормаль-

		ный вектор	плоскости		(2) n = (A; B;C)
		(рис. 1). Тогда	æ π
			æ π		ö	= sinα .	(3)
		cos(n,a)	= cosç	-α ÷		= sinα .	(3)
			è 2		ø
Рис. 1		Используя (3)		и	формулу		(9.2),
Рис. 1		заключим, что
		заключим, что
	sinα =	\| Al + Bm + Cn \|			.		(4)
	sinα =				.		(4)

A2 + B2 + C2 l2 + m2 + n2

Прямая (1) параллельна плоскости (2) тогда и только тогда, когда направляющий вектор этой прямой a перпендикулярен нормальному вектору n данной плоскости.

Отсюда получаем условие параллельности прямой (1) и плоскости (2):

Al + Bm + Cn = 0 .

(5)

Прямая (1) перпендикулярна плоскости (2) в том и только том случае, когда направляющий вектор a этой прямой коллинеарен нор- мальному вектору n плоскости, что равносильно следующему равенству:

A	=	B	=	C	.	(6)
l		m
				n

Найдем теперь условия, при которых прямая (1) принадлежит плоскости (2). Это будет тогда и только тогда, когда одновременно будут выполняться два равенства:

Ax0	+ By0 + Cz0	+ D = 0,	(7)
Al + Bm + Cn = 0,			(7)
Al + Bm + Cn = 0,
где первое из равенств (7)	означает,	что точка M0 (x0; y0; z0 ) , через

которую проходит прямая (1), принадлежит плоскости (2), а второе равенство из (7) выражает условие параллельности прямой (1) и плос- кости (2).

Пример 1. Составить уравнение прямой, проходящей через начало координат и перпендикулярной прямой x -2 2 = y3-1 = z 1- 3 .

Решение. Используя условие перпендикулярности прямой и плоскости (6) и полагая, что A = l, B = m, C = n, D = 0 , составим урав-

нение плоскости, проходящей через начало координат и перпендику- лярной заданной прямой. Оно имеет вид 2x + 3y + z = 0 . Найдем точку

134

пересечения плоскости и данной прямой. Параметрические уравнения прямой запишутся так: x = 2t + 2, y = 3t +1, z = t + 3. Для определения

t имеем уравнение 2(2t + 2) + 3(3t +1) + t + 3 = 0 , откуда t = - 5

. Коор-

æ 4

16 ö

динаты точки пересечения x =

, y = -

, z =

т.е. M ç

;

÷ .

è 7

7 ø

Составим теперь уравнения прямой, проходящей через начало

координат и точку М, используя уравнения (8.3/):

или

. □

4 ö

æ16

-2

7 ø

è 7

Пример 2. Исследовать взаимное расположение прямой x = 4 + 3t,

y = 6 + 4t, z = 5 + 2t

и плоскости 2x - 3y + 5z -10 = 0.

Решение. Поскольку имеем 2 ×3 + (-3) × 4 + 5× 2 = 4 ¹ 0,

т.е. усло-

вие (5) не выполняется, прямая и плоскость пересекаются. Найдем

точку их пересечения, для чего подставим выражения

для x, y, z

в уравнение плоскости:

2(4 + 3t) - 3(6 + 4t) + 5(5 + 2t) -10 = 0,

4t + 5 = 0, t = -

Подставив полученное значение параметра в уравнение прямой,

найдем координаты точки пересечения:

5 ö

. □

x = 4 + 3×ç -

, y = 6 + 4 ×ç -

÷ =1, z

= 5 + 2 ×ç -

4 ø

§ 11. Эллипс и его каноническое уравнение

Эллипсом называется множество точек плоскости, сумма рас- стояний от каждой из которых до двух заданных точек F1 и F2 , назы-

ваемых фокусами, есть величина постоянная, равная 2a .

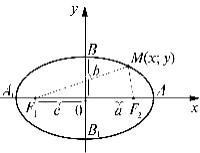
Выведем уравнение эллипса. Для этого выберем декартову систе- му координат Oxy так, чтобы ось

Ox проходила через фокусы F1 и F2 , расстояние между которыми обозначим 2c , а начало координат О находилось в середине отрезка F1F2

Рис. 1

(рис. 1).

135

Тогда фокусы будут иметь координаты: F1(-c;0) и F2 (c;0) (рис. 1). Если M (x; y) – произвольная точка эллипса, то согласно его определению, имеем:

MF1 + MF2 = 2a .

(1)

По формуле расстояния между двумя точками имеем

MF =

= (x + c)2 + y2 ,

MF =

= (x - c)2 + y2 .

(2)

Подставляя (2) в (1), будем иметь

(x + c)2 + y2 +

(x - c)2 + y2 = 2a .

(3)

Уравнение (3) и есть уравнение эллипса. Приведем его к так

называемому каноническому виду. Из (3) имеем

(x + c)2 + y2 = 2a - (x - c)2 + y2 .

Возведя обе части последнего равенства в квадрат, получим

x2 + 2xc + c2 + y2 = 4a2 - 4a (x - c) + y2 + x2 - 2xc + c2 + y2 .

Отсюда

a (x - c)2 + y2 = a2 - cx ,

(4)

или, возведя обе части равенства (4) в квадрат, будем иметь

a2 x2 - 2a2cx + a2c2 + a2 y2 = a4 - 2a2cx + c2 x2 .

(5)

Из (5) получаем

(a2 - c2 )x2 + a2 y2 = a2 (a2 - c2 ) .

(6)

Так как a > c , то a2 - c2 > 0 . Обозначим b =

a2 - c2 , тогда (6)

примет вид

b2 x2 + a2 y2 = a2b2 .

(7)

Разделив обе части (7) на a2b2 , получим уравнение эллипса вида:

=1.

(8)

Показано, что любая точка эллипса удовлетворяет уравнению (8).

Покажем теперь обратное: любая точка

M (x; y) ,

удовлетворяющая

уравнению (8), принадлежит эллипсу, т.е. удовлетворяет соотно- шению (1). Из уравнения (8) получаем

y2	= b2	æ	-	x	2	ö
		ç1				÷.
					2
		ç		a		÷
		è				ø

Используя это соотношение и учитывая, что b2 = a2 - c2 , находим

136

= x2 + 2cx + c2 + b2 -

x2 =

x2 + 2cx + a2 =

MF = (x + c)2 + y2

æ c

ö2

x + a ÷ =

a +

è a

Так как, в силу равенства (8),

£ a и,

кроме того, c < a , то

MF1 = a + ac x.

Аналогично можно получить формулу MF2 = a - ac x. Складывая

последние два равенства, получаем равенство (1).

Итак, соотношение (8) является уравнением эллипса. Оно называется каноническим уравнением эллипса. Такой эллипс изобра-

жен на рис. 1. Эллипс симметричен относительно обеих осей коорди-

нат. Из уравнения (8) при y = 0 получаем: x = ±a , т.е. эллипс пересе-
кает ось Ox	в двух точках: A(a;0) и	A1(-a;0) ; при x = 0 получаем:
y = ±b , т.е.	эллипс пересекает ось	Oy в	двух точках: B(0;b) и
B1(0;-b) . Эти четыре точки называют вершинами эллипса. Отрезок A1A
называется большой осью эллипса, а отрезок			B1B – его малой осью.
Значит, a – длина большой полуоси эллипса,			b – длина малой полу-
оси эллипса.
Уравнение (8) можно рассматривать и в случае a < b, оно опре-
деляет эллипс с большой полуосью		OB = b,	фокусы такого эллипса
лежат на оси Oy.
В том случае, когда a = b , уравнение (8) имеет вид x2 + y2 = a2

и определяет окружность радиуса а с центром в начале координат. В этом случае c = 0 .

Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси, т.е.

ε =

(9)

Поскольку c < a , то для любого эллипса 0 ≤ ε <1, причем случай

ε = 0 соответствует окружности.

Геометрически

характеризует

степень сжатия эллипса.

Действительно,

из

(9)

и равенства

b2 = a2 - c2 вытекает, что

ε 2

a2 - b2

æ b ö2

=1- ç

÷ .

è a ø

137

Значит,
	b
	b	= 1− ε 2 .	(10)
	a	= 1− ε 2 .	(10)
	a		b
Из (10) видно, что чем больше ε , тем меньше отношение			b	и
Из (10) видно, что чем больше ε , тем меньше отношение			a	и
			a

тем больше вытянут эллипс. Две прямые, перпендикулярные большой

оси эллипса и расположенные симметрично относительно центра на

расстоянии	a	от него, называются директрисами эллипса.
расстоянии	ε	от него, называются директрисами эллипса.
	ε
Если эллипс задан каноническим уравнением (8), то уравнения
директрис имеют вид
		x = −	a	и x =	a	.	(11)
		x = −	ε	и x =		.	(11)
			ε		ε

Так как ε <1 , то εa > a . Откуда заключаем, что правая директриса

расположена правее правой вершины эллипса, а левая – левее его левой вершины. Важность понятия директрис будет установлена позднее.

Пример 1. Найти параметры эллипса, заданного уравнением


x2	+		y2		= 2 .
9	+	4			= 2 .
9		4
			Решение. Приведем данное уравнение к каноническому виду
x2	+		y2			=1. Отсюда вытекает, что a = 3					, b = 2						, c =					=		,
x2			y2							2					2				18 − 8				10
18		8								2					2				18 − 8				10
18		8
ε =			10			=		5	. Уравнения директрис:	x = −		9		10		, x =		9		10	. □
	3						3						5						5
	3			2			3						5						5

§ 12. Гипербола и ее каноническое уравнение

Гиперболой называется множество точек плоскости, модуль раз- ности расстояний от каждой из которых до двух заданных точек F1 и F2 ,

называемых фокусами, есть величина постоянная, равная 2a < F1F2 . Пусть 2c – расстояние между фокусами F1 и F2 . Выберем декартову систему координат Oxy так, чтобы F1 и F2 находились

на оси Ox симметрично относительно начала координат (рис. 1). Если M (x; y) – произвольная точка гиперболы, то, по опреде-

лению,

138

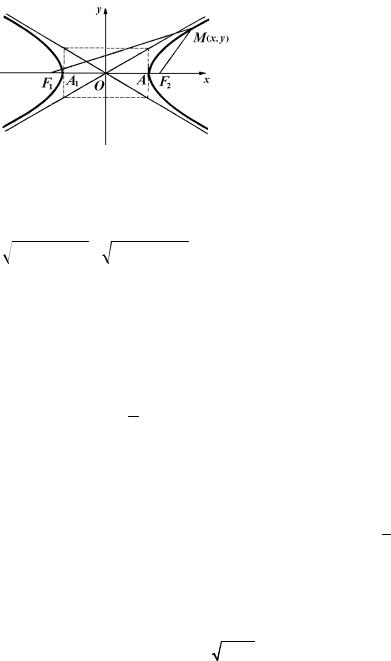
MF1 - MF2 = 2a или MF2 - MF1 = -2a .

Эти условия можно запи-

	сать так:
				MF1 - MF2 = ±2a .
				Отметим, что		a < c , так
	как			из треугольника F1MF2
	имеем 2a < 2c .
				Рассуждая аналогично, как
	и при выводе канонического
	уравнения эллипса, получим ка-
Рис. 1	ноническое уравнение гиперболы
		x2		y2
			-		=1, где b2 = c2 - a2 .(1)
		a2
				b2
Упражнение 1. Доказать эквивалентность канонического
уравнения (1) с иррациональным				уравнением		гиперболы

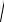(x + c)2 + y2 - (y - c)2 + y2 = ±2a.

Такая гипербола изображена на рис. 1. Она симметрична отно- сительно обеих осей координат и состоит из двух частей, которые называют ее ветвями.

Если y = 0 , то из уравнения (1) получаем x = ±a , т.е. гипербола пересекает ось Ox в двух точках: A(a;0) и A1(-a;0) , называемых

вершинами гиперболы. Отрезок A1A = 2a называется действительной осью гиперболы, а отрезок B1B = 2b – мнимой осью.

Прямые y = ± ba x называются асимптотами гиперболы, к кото-

рым приближаются ветви гиперболы при увеличении х по абсолютной величине. Для их построения целесообразно предварительно построить прямоугольник со сторонами 2а и 2b, параллельными координатным осям и с центром в точке О (рис.1), который называют еще основным прямоугольником гиперболы.

Эксцентриситетом гиперболы называют отношение ε = ac . Так как

а < с, то для любой гиперболы ε >1 . С учетом b2 = c2 - a2 , получаем

ε 2

+ b2

æ b ö2

=1+ ç

÷ .

Отсюда

è a ø

= ε 2 -1 .

(2)

139

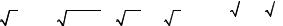
Из (2) видно, что, чем меньше ε , т.е. чем ближе ε к единице, тем больше вытянут основной прямоугольник по оси Ох.

Если у гиперболы (1) a = b , то она называется равносторонней

или равнобочной и ее уравнение принимает вид

x2 − y2 = a2 .						(3)
Асимптотами этой гиперболы являются взаимно перпендику-
лярные прямые y = ±x .
Уравнение
−	x2	+	y	2	=1	(4)
−	a2	+	b2		=1	(4)
	a2		b2

определяет гиперболу с действительной осью Oy.

Гиперболы, определяемые уравнениями (1) и (4) в одной и той же системе координат с одинаковыми значениями a и b , называются

сопряженными.
Две прямые, заданные уравнениями
x = −	a	и x =			a	,	(5)
x = −		и x =			ε	,	(5)
	ε				ε
называют директрисами гиперболы (1).
Так как для гиперболы ε >1 , то			a	< a и из (5) следует, что правая
Так как для гиперболы ε >1 , то			ε	< a и из (5) следует, что правая
			ε

директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной гиперболы.

Пример 1. Найти параметры гиперболы, заданной уравнением

x2 − 2y2 =16 .

Решение. Приведем данное уравнение к каноническому виду

−

=1 . Отсюда получаем, что

a = 4, b = 2 2, c = 16 + 8 =

24 = 2 6, ε =

. □

§ 13. Парабола и ее каноническое уравнение

Параболой называется множество точек плоскости, равноуда- ленных от данной точки F, называемой фокусом, и от данной прямой L,

называемой директрисой.

Для вывода канонического уравнения параболы выберем декар- тову систему координат Оху так, чтобы ось Ох проходила через фокус

140

F перпендикулярно директрисе, а на- чало координат О поместим на одина- ковых расстояниях от фокуса и дирек- трисы (рис.1).

Расстояние от фокуса до дирек- трисы, называемое параметром пара- болы, обозначим через р. Тогда фокус

имеет координаты

F ç

, а уравне-

нием директрисы является x = -

Рис. 1

Пусть М(х;у) – произвольная

точка параболы. Тогда, согласно ее определению, имеем

MF = MA .

(1)

Точка А имеет координаты çæ -

; y

÷ö . Имеем

p ö2

ö2

MF =

ç x -

+ y2 ,MA =

ç x +

(2)

2 ø

Из (1) и (2) получаем

ö2

+ y2

p ö2

ç x -

ç x +

÷ .

(3)

p ö2

Отсюда ç x -

+ y

ç x +

или

2 ø

x2 - px +

+ y2

= x2

+ px +

. Окончательно получаем

y2 = 2 px .

(4)

Уравнение (4) называется каноническим уравнением параболы,

изображенной на рис. 1.

Упражнение 1. Установить равносильность уравнений (3) и (4).

Отметим, что уравнение (4) имеет смысл только для неотрица- тельных значений х, т.е. все точки параболы лежат в I и IV квадрантах. Уравнение (4) не меняется при замене у на –у, т.е. парабола симмет- рична относительно оси Ох.

Точка О называется вершиной параболы, ось симметрии (ось Ох)– осью параболы. Выясним геометрический смысл параметра па-

141

раболы р. Для этого возьмем x =1 и найдем из уравнения (4) соответ- ствующие значения ординаты y = ±2 p . Получаем на параболе две,


симметричные			относительно ее оси, точки M1 (1;+				) и
						2 p
M2 (1;−		).	Расстояние между ними равно 2		. Отсюда заклю-
	2 p			2 p

чаем, что это расстояние тем больше, чем больше р, т.е. параметр р характеризует «ширину» области, ограниченной параболой.

Парабола, уравнение которой y2 = −2 px, p > 0 , расположена

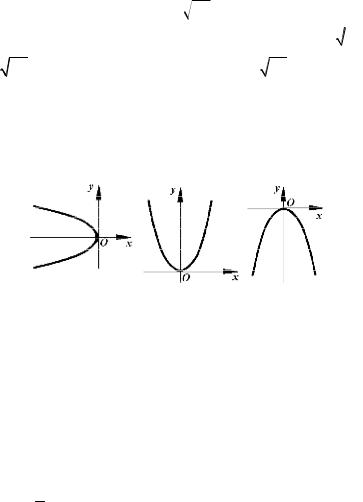
слева от оси ординат (рис. 2а)). Ее вершина совпадает с началом коор- динат О, осью симметрии является ось Ох.

Рис. 2 а)	Рис. 2 б)	Рис. 2 в)
Уравнение x2 = 2 py,	p > 0 , является уравнением параболы с

вершиной в точке О и осью симметрии Оу (рис.2б)). Такая парабола лежит выше оси абсцисс. Уравнение x2 = −2 py, p > 0 , определяет

параболу, которая лежит ниже оси Ох, с вершиной в точке О и осью симметрии Оу (рис.2в)).

Пример 1. Парабола с вершиной в начале координат проходит через точку М0(3;1) и симметрична относительно оси Оу. Написать ее каноническое уравнение.

Решение. Подставляя координаты точки M0 в уравнение x2 = 2 py ,

находим p = 92 . Значит, уравнение искомой параболы x2 = 9y . □

§ 14. Общее уравнение кривых второго порядка

Одной из основных задач аналитической геометрии является исследование уравнения линии второго порядка и приведение его к простейшим формам.

Рассмотрим сначала преобразование декартовых координат на плоскости.

142

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 6014 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20181.61 Mб16Маркетинг 1-18,24-27.doc
#
18.02.201698.41 Кб50Маркетинг готовые шпоры.docx
#
14.04.201960.88 Кб3Мат логіка 2 курс 3 семестр.docx
#
12.08.20192.49 Mб37Мат Моделирование (конспект).doc
#
18.02.20162.81 Mб110Математика для инженеров(практика) I часть.pdf
#
18.02.20164.09 Mб103Математика для инженеров(теория)I том.pdf
#
18.02.20161.05 Mб68Математика шпоры заочники.docx
#
27.09.2019302.06 Кб5МАТЕМАТИКА ШПОРЫ.docx
#
19.11.2019602.11 Кб2материал хоз процесс.doc
#
18.02.2016217.6 Кб77Материалы для шпор.doc
#
22.11.201962.98 Кб3Материалы к зачету ЭУП, ПЛ з.о. 1 сем.doc