Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика для инженеров(теория)I том

.pdf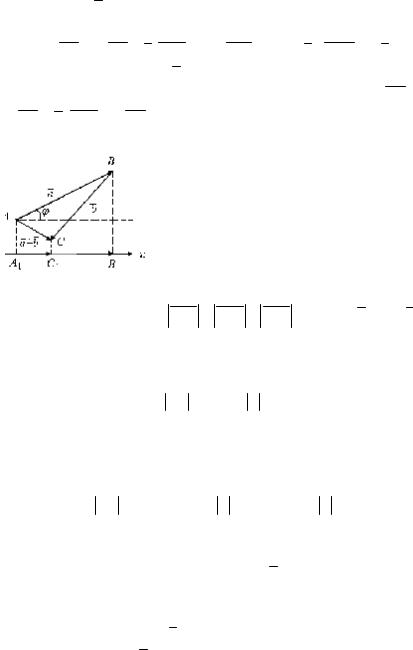

Скачиваний:

103

Добавлен:

18.02.2016

Размер:

4.09 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 6010 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

векторы a и b неколлинеарны, то свойство 5) вытекает из подо- б и я т р е у г о л ь н и к о в А В С и AB1C1 ( р и с . 3 а ) , г д е

AB = a, BC = b , AB 1 = α a, AC1 = α(a + b ), B 1C1 = α b.

Если векторы a и b коллинеарны, то свойство 5) вытекает из подобия треугольников АСВ и AC1B1 (рис. 3 б)), где CD = a,

DB = b , AC1 = α AC. При α < 0 свойство 5) проверяется аналогично, а при α = 0 оно очевидно. □


	Докажем, что для проекций векто-
	ров a и		на ось u справедливы сле-
		b
		дующие равенства:
	npu (a +				) = npua + npu		,	(1)
				b		b
	npu (α a) = α npu a, α .							(2)
	Доказательство. Формула (1) выте-
Рис. 4	кает из определений проекции вектора
	на ось и суммы векторов (рис. 4). Дейст-

вительно, имеем npu a = A1B1 = A1C1 + C1B1 = npu (a + b ) − npub , от-

куда и получаем (1).

Докажем формулу (2). Пусть ϕ = . Если α > , то с уче-

(a,u) 0

том формулы (3.1) имеем

npu (α a) = α a cosϕ = α a cosϕ = α npu a .

Если α < 0 , то векторы a и α a направлены противопо-

ложно и, значит,

(αa,u) = π −ϕ.

Тогда

npu (α a) = α a cos(π −ϕ) = −α a cos(π −ϕ) = α a cosϕ = α npu a .

При α = 0 равенство (2) очевидно. □

Из формулы (2) вытекает, что если a = (X ;Y;Z) , то α a = (α X ;α Y;αZ), т.е. векторы a и b коллинеарны в том и

только том случае, когда их координаты пропорциональны. Из формулы (1) получаем, что если a = (X1;Y1;Z1) и

b = (X2;Y2;Z2 ), то

a + b = (X1 + X2; Y1 + Y2; Z1 + Z2 ) . □

§ 6. Разложение вектора по базису

Рассмотрим декартову систему координат Охуz. Пусть

i , j , k – единичные векторы соответствующих осей координат Ох,

Оу, Оz,

т.е.

=1, и каждый из них

одинаково направлен с соответст-

вующей осью координат (рис. 1).

Тройка векторов

называется

базисом.

Теорема 1. Любой вектор a

можно единственным образом разло-

жить по базису

, т.е. предста-

в и

в и д

a = ax

+ ay

+ az

(1)

Рис. 1

где ax , ay , az - числа.

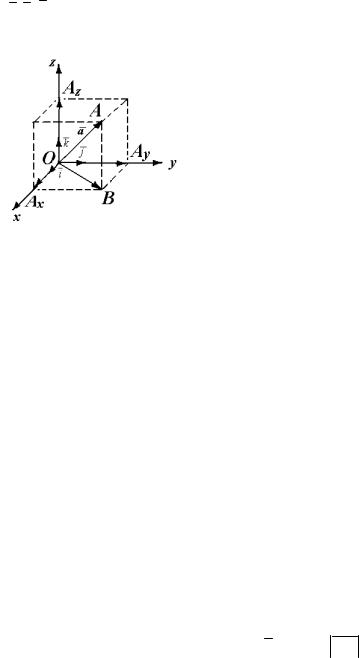
Доказательство. Отнесем вектор a к началу координат и обо-

значим его конец через А. Проведем через точку А плоскости, перпендикулярные осям координат и обозначим через

Ax , Ay , Az – точки пересечения их с соответствующими осями ко-

ординат. По определению сложения векторов, имеем

a =

OAz

OAx

OAy

. Значит,

a =

(2)

OAx

OAy

OAz

Так как векторы

коллинеар-

OAx

OAy

OAz

= ax

= ay

= az

(3)

OAx

OAy

OAz

где ax , ay , az – числа.

Из равенства (2 ) и соотношений

(3 ) получаем

a = ax

+ ay

+ az

Для доказательства единственности представления (1) по-

кажем, что ax = X ,

ay = Y,

az = Z , где X ,Y , Z –

координаты век-

Покажем, например, что ay = Y. Так как Y =

, если

OAy

имеет то же направление, что и вектор j , и Y = − OAy , если вектор

OAy имеет направление, противоположное направлению вектора j ,

то OAy = Y j . Согласно этому равенству и второй из формул (3),

получаем ay = Y. Аналогично доказывается, что ax = X , az = Z. □

§ 7. Скалярное произведение векторов

10. Определение скалярного произведения, его свойства и ме-

ханический смысл. Скалярным произведением a ×b двух ненулевых

векторов a и b называется число, равное произведению длин

векторов на косинус угла между ними. Если хотя бы один из век-

торов a и

нулевой, то скалярное произведе-

ние равно нулю.

Таким образом,

a ×

cosϕ,

(1)

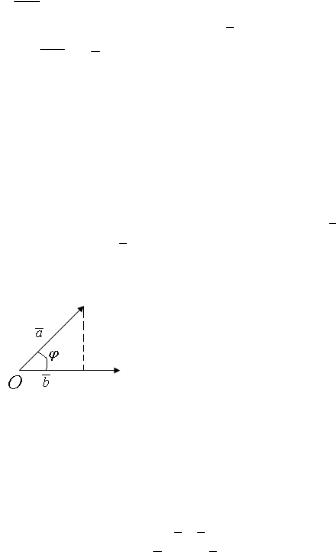
где ϕ – угол между векторами a и

(рис. 1).

Рис. 1

Скалярное произведение обозначают

символом a ×

, или (

) , или

ab .

По формуле (3.1)

cosϕ = np

cosϕ = npa

, поэтому вы-

ражение (1) можно записать:

a ×

a =

npa

(2)

Для скалярного произведения векторов справедливы сле-

дующие свойства:

1)a ×b = b × a – коммутативность;

2)(λ a) ×b = λ (a ×b ) – ассоциативность, λ ;

	3) (a +		) ×c = a ×c +		×c	– дистрибутивность;
	3) (a +	b	) ×c = a ×c +	b	×c	– дистрибутивность;
			4) a × a =				a	2 .
			4) a × a =				a	2 .
	Доказательство. Коммутативность скалярного произведения
	непосредственно вытекает из формулы (1).
	Докажем свойство 2). С учетом формул (2) и (5.2), будем
и	м		е					т	ь

(λ a) ×

λ np

a = λ (

a) = λ (a ×

(3)

Доказательство свойства 3). По формуле (2)

(a +

) ×c =

npc (a +

(4)

Согласно формуле (5.1),

npc (a +

) = npc a + npc

Таким образом, с учетом (4) и формулы (2), получаем

(a + b ) ×c = c (npc a + npc b ) = c npc a + c npc b = a ×c + b ×c.

Для доказательства свойства 4) заметим, что по формуле (1) a × a = a a cos0 = a 2 , если a ¹ 0 , т.е. если a ¹ 0 . Если же a = 0 , то

также, по определению скалярного произведения, a × a = 0. Но, тогда a = 0 и, поэтому, равенство a × a = a 2 в случае a = 0 также

справедливо. □

Скалярное произведение a × a называется скалярным квадратом вектора a и обозначается a2 . На основании свойства 4)

имеем: a2 = a 2 , отсюда, в частности, a 2 = a .
Из свойств 1) и 2) вытекает, что
(λ a) ×(μ b ) = (λμ) ×(a ×b ), λ,μ Î .	(5)

Из свойства 3) следует, что при скалярном умножении векторных многочленов можно выполнять действия почленно и, в силу (5), объединять коэффициенты векторных сомножителей.

Пример 1. Найти скалярное произведение (3a + 7b ) ×(4c + 5d ).

Решение. Имеем

(3a + 7b ) ×(4c + 5d ) = (3a) ×(4c + 5d ) + (7b ) ×(4c + 5d ) = = (3a) ×(4c ) + (3a) ×(5d ) + (7b ) ×(4c ) + (7b ) ×(5d ) =

=12a ×c +15a × d + 28b ×c + 35b × d.

Выясним механический смысл скалярно-

го произведения. Из физики известно, что ра-

бота А, совершаемая силой

при перемеще-

нии

, равна произведению величины этой си-

лы на величину перемещения: A =

, если

Рис. 2

направление силы совпадает с направлением

перемещения.

Если сила направлена под углом α к направлению дви-

жения (рис. 2), то на тело оказывает влияние составляющая


	OD силы	F	, которая направлена по прямой перемещения.
П е р			п е н д и к у л я р н а я

составляющая компенсируется сопротивлением.						Поэтому
(	р	и	с	.	2	)

A = S × ( F cosα) = S OD = S ×OD = S F cosα.

Таким образом, скалярное произведение двух векторов численно равно работе некоторой силы при перемещении тела.

20. Условие перпендикулярности двух векторов. Угол между двумя векторами. Сформулируем необходимое и достаточное усло-

вие перпендикулярности двух векторов.

Свойство 5). Два ненулевых вектора a и

перпендикуляр-

ны тогда и только тогда, когда их скалярное произведение a ×

рав-

Доказательство. Необходимость. Пусть ϕ =

(a,b ) =

a ¹ 0,

¹ 0 . Тогда cosϕ = 0 и a ×

cos

π = 0.

Достаточность. Пусть a ×

= 0 и a ¹ 0,

¹ 0. Используя

формулу (1), получаем

cosϕ = 0 лишь если cosϕ = 0 или

ϕ = π

. Значит, a ^

□

Из равенства (1) получаем формулу для определения коси-

нуса угла между ненулевыми векторами:

cosϕ =

a ×

(6)

Отметим, что из свойств 4) и 5) для базисных векторов

непосредственно получаем следующие равенства:

2 =

2 =1,

= 0.

(7)

30. Выражение скалярного произведения через координаты век-

торов. Если векторы a и

заданы своими координатами:

a = (X1;Y1;Z1), b = (X2;Y2;Z2 ) , то их скалярное произведение вы-

числяется по формуле


a ×		= X1X2 + Y1Y2 + Z1Z2 .		(8)
a ×	b	= X1X2 + Y1Y2 + Z1Z2 .		(8)
Доказательство. Разложим векторы a и				по базису		,		,
			b						k
			b		i		j		k
согласно формуле (6.1):

a = X1i + Y1 j + Z1k , b = X2i + Y2 j + Z2k .


Тогда													2 + X Y																													2
a ×					= X			X													+ X			Z						+ Y X								+ Y Y					+
			b																										k
							1		2		i						i		j				1		2	i							2		j		i				j
											1					2										1													1	2					. (9)
+Y Z						+ Z X									+ Z Y							+ Z Z						2 = X				X				+ Y Y				+ Z Z
				k								k						k									k
	2	j								2				i						j					2						1			2										2
1							1				1					2							1													1			2	1

Из формулы (8) и свойства 5) вытекает необходимое и доста-

точное условие перпендикулярности ненулевых векторов

a = (X1;Y1;Z1) и b = (X2;Y2;Z2 ) : сумма произведений одноименных

координат этих векторов равна нулю, т.е.

X1X2 + Y1Y2 + Z1Z2 = 0 .

(10)

Пример 2. Даны три точки A(2;2;2), B(3;1;1), C(2;0;5). Найти

ÐABC .

Решение. Имеем

= (1;-1;-1);

= (0;- 2;3). По формуле

(6), с учетом (8), получаем

cosÐABC =

1×0 + (-1)(-2) + (-1) ×3

-1

= -

12 + (-1)2 + (-1)2 × 02 + (-2)2 + 32

ÐABC = arccos(-

) = π - arccos(

) .

□

§ 8. Векторное произведение векторов

10. Ориентация тройки векторов в пространстве. Тройку

векторов называют упорядоченной, если указано, какой из векторов считается первым, какой вторым и какой третьим. В записи

(a;b;c ) вектор a считается первым, b – вторым, c – третьим; в записи (c;b;a) вектор c – первый, b – второй, a – третий.

Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу кратчайший

поворот от первого ко второму вектору наблюдается с конца третьего вектора против часовой стрелки. В противном случае указанная тройка векторов называется левой.

20. Векторное произведение двух векторов, его свойства, гео- метрический и физический смысл. Векторным произведением век-

торов a и b называется вектор c , длина которого численно рав-

на площади параллелограмма, построенного на векторах a и b ,

приведенных к общему началу, который перпендикулярен пере-

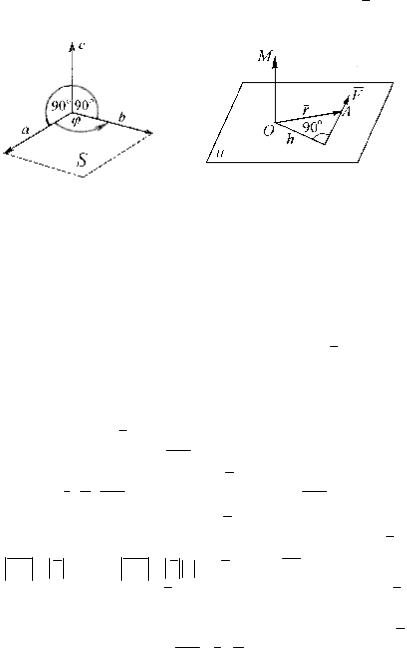
множаемым векторам и направлен так, что векторы a,b ,c обра-

зуют правую тройку векторов (рис. 1).

Рис. 1		Рис. 2
Если векторы a и		коллинеарны, то их векторное произве-
	b

дение равно нулевому вектору.

Из определения векторного произведения следует, что

(

)

sinϕ = S ,

(1)

где ϕ –

угол между векторами a и

, S – площадь параллело-

Векторное произведение двух векторов a и b обозначают

символом

	é	ù	é	ù

a ´b , или ëa b û			, или ëa,b û .

Выясним физический смысл векторного произведения. В фи-

зике момент силы F с точкой приложения А относительно точки

О изображают вектором OM , перпендикулярным плоскости, в которой лежат точка О и вектор F (рис. 2), таким, что тройка векторов r, F, OM – правая. Длина вектора OM определяется как произведение длины вектора F на плечо h , где h – расстояние от точки О до прямой, на которой лежит вектор силы F , т.е.

= × = =

OM F h , или OM F r sin(F,r ), (r OA – радиус–вектор

точки приложения силы F) . Таким образом, момент силы F относительно некоторой точки O , есть векторное произведение ра- диус–вектора r точки приложения силы на вектор силы F :

OM = r ´ F .

Свойства векторного произведения.

1. При перестановке сомножителей векторное произведение ме-

няет знак (антикоммутативность), т.е.

a ×

= −(

× a) .

(2)

Доказательство. Если векторы a и

коллинеарны, то ра-

венство (2) очевидно, т.к. a ×

× a – нулевые векторы.

Пусть a и

неколлинеарны.

Из определения векторного произ-

ведения вытекает, что векторы

a ×

× a имеют одинаковые

длины и коллинеарны, но направ-

лены противоположно (рис. 3), т.к.

векторы a,

,a ×

,a,

× a обра-

Рис. 3

Рис. 4

зуют правые тройки. Значит,

a ×

= −(

× a) . □

2. Ассоциативность:

(α a) ×

= α(a ×

), α .

(3)

Для доказательства равенства (3) используем следующие

рассуждения. Векторы (α a) ×

и α(a ×

) имеют одинаковую

длину, т.к. при α > 0 получаем

(α a) ×

α a

sinϕ = α

a ×

;

при α < 0 имеем

(α a) ×

α a

sin(π −ϕ) = −α

sinϕ = −α

a ×

где ϕ = (a,b ). Кроме того, рассматриваемые векторы одинаково

направлены (рис. 4). Действительно, при α > 0 оба имеют то же

направление, что и вектор a ×

, а при α < 0 – противоположное.

Если α = 0 , то равенство (3) очевидно. □

Упражнение 1. Используя свойства 1 и 2, доказать, что

a × (α

) = α (a ×

) .

(4)

3. Дистрибутивность:

(a +

) × c = a × c +

× c .

(5)

Доказательство.

Если векторы a и

коллинеарны вектору

или хотя бы один из векторов a,

,c нулевой,

то формула (5)

100

Докажем, что формула (5) справедлива, если в качестве векто-

ра c в ней рассматривается единичный вектор c 0 = cc . Для этого

осуществим соответствующее построение (рис. 5). Проведем через начало вектора c 0 плоскость П, перпендикулярную этому вектору и рассмотрим треугольник ОАВ, в котором OA = a, AB = b , OB = a + b.

Спроектируем треугольник ОАВ на плоскость П, в результате получим треугольник OA1B1 .

Рис. 5

Повернем в плоскости П каждый из векторов OA1, A1B1, OB1

на угол 90o вокруг точки О по часовой стрелке, если смотреть с

конца вектора c 0 . Тогда треугольник OA B займет положение

треугольника OA2B2 . Обозначим через ϕ угол между векторами

c 0 и a . Пусть, для определенности 0 < ϕ < π

, как на рис. 5. Тогда

ÐAOA = π -ϕ . Остальные случаи угла ϕ рассматриваются ана-

логично.

Рассмотрим вектор

. Длина его

OA2

cos(π -ϕ) = =

c 0

sinϕ , т.к.

c 0

=1. Далее

OA2 ^c 0 , OA2 ^a и векторы a,c 0 ,OA2 образуют правую тройку, тогда OA2 = a ´ c 0 .

Если вектор b перенести в точку О, то, используя аналогичные рассуждения, получаем A2B2 = b ´ c 0 . Аналогично получа-

ем OB2 = (a + b ) ´ c 0. Но, так как OB2 = OA2 + A2B2 , то

101

(a +

) ´ c 0 = a ´ c 0 +

´ c 0.

( 5′ )

Вектор c направлен так же, как c 0 . Поэтому c =

×c 0.

Умножим обе части равенства ( 5′ ) на

, получим

c ((a + b ) ´ c 0 )= c (a ´ c 0 + b ´ c 0 ). Отсюда, согласно свойству 2, (a + b ) ´ c c 0 = a ´ c c 0 + b ´ c c 0. Заменяя здесь c c 0 на c , получа-

ем формулу (5). □

	Упражнение 2. Используя формулу (5) и свойство 1, доказать,
ч			т			о
	a ´ (		+ c ) = a ´		+ a ´ c.	(6)
		b		b

Отметим, что формулы (3) – (6) позволяют при векторном умножении векторных многочленов выполнять действия почленно и объединять числовые коэффициенты векторных сомножите-

лей. Например,

(3a + 7b )´ (6c + 5d ) = (3a + 7b ) ´ 6c + (3a + 7b ) ´5d =

=3a ´ 6c + 7b ´ 6c + 3a ´5d + 7b ´5d =

=18(a ´ c ) + 42(b ´ c ) +15(a ´ d ) + 35(b ´ d ). □

4. Векторное произведение a ´b = 0 , ес-
ли a и b – коллинеарные векторы.
Доказательство. Если векторы a и b
коллинеарны, то sinϕ = 0. Поэтому,
a ´b = a b sinϕ = 0 , т.е. длина вектора
Рис. 6	равна нулю,
a ´b
а значит, и сам вектор a ´b	равен нулю. □
Согласно определению и свойствам 1, 4 векторного произведе-

ния, получаем следующие равенства для базисных векторов i , j ,k

(

)

= 0;

;

= -

;

= -

;

= 0;

;

(7)

;

= -

;

= 0.

30. Векторное произведение в координатной форме. Условие коллинеарности векторов. Пусть векторы a и b заданы своими

102

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 6010 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20181.61 Mб16Маркетинг 1-18,24-27.doc
#
18.02.201698.41 Кб50Маркетинг готовые шпоры.docx
#
14.04.201960.88 Кб3Мат логіка 2 курс 3 семестр.docx
#
12.08.20192.49 Mб37Мат Моделирование (конспект).doc
#
18.02.20162.81 Mб110Математика для инженеров(практика) I часть.pdf
#
18.02.20164.09 Mб103Математика для инженеров(теория)I том.pdf
#
18.02.20161.05 Mб68Математика шпоры заочники.docx
#
27.09.2019302.06 Кб5МАТЕМАТИКА ШПОРЫ.docx
#
19.11.2019602.11 Кб2материал хоз процесс.doc
#
18.02.2016217.6 Кб77Материалы для шпор.doc
#
22.11.201962.98 Кб3Материалы к зачету ЭУП, ПЛ з.о. 1 сем.doc