1. Понятие матрицы. Линейные операции над матрицами. Произведение ит ранспонирование матриц. Матрицей размером m×n наз-ся совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Для краткости матрицу обозн-т заглавн.букв. А. a_ij: i-строка, j-столбец. Квадратная матр. – число строк равно числу столбцов. Матрица, состоящая из одной строки или столбца – вектор. Нулевая матрица – матрица, все элементы кот-й равны нулю. Треугольная матрица – квадратная матрица, у кот-й все элементы, лежащие ниже главной диагонали, равны нулю. Диагональная матрица – квадратная матрица, у кот-й все элементы, кроме главной диагонали, равны нулю. Единичная матрица (обозн-ся E) – диагональная матрица, у кот-й диагональные элементы равны единице. Линейные операции: сложения элементов матриц и умножения матриц на число. Сложение возможно только для матриц одинаковых размеров. Результатом сложения матриц A = || ai j || и B = || bi j || является матрица C = || ci j || , элементы кот-й равны сумме соответствующих матричных элементов. При умножении матрицы A на число каждый ее элемент умножается на это число.Произведение. Перемножать можно только те матрицы, у кот-х число столбцов первой матрицы совпадает с числом строк второй матрицы. Произведением матрицы A на B наз-ся новая матрица C=AB, элементы кот-й составляются след. образом:.

Элементы матрицы-произведения – сумма произведения строк первой матрицы на столбцы второй матрицы. Перемножая две квадратные матрицы одного порядка, получаем квадратную матрицу того же порядка. Квадратную матрицу можно умножить саму на себя, т.е. возвести в квадрат.

Перемноженая векторы, причём ширина первого д.б. равна высоте второй, получаем матрицу первого порядка (т.е. один элемент):

.

A∙B ≠ B∙A – операция умножение неперестановочная

(AB)C=A(BC) и (A+B)C=AC+BC

AE=EA=A

Произведение 2-х не нулевых матриц может оказаться равным нулевой матрице:

Транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу A^T наз-т транспонированной к матрице A, если столбцы А записать в строчку.

2. Определители 2 и 3-го порядков. Вычисление определителя n-го порядка. Свойства определителей 3-го порядка.

Вычисление определителей второго порядка.

Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:

Запомнить просто: произведение элементов, стоящих на главной диагонали, минус

произведение элементов, стоящих на побочной.

Вычисление определителей третьего порядка.

Определитель третьего порядка вычисляется по правилу:

Запомнить порядок сомножителей, конечно же, очень трудно, если не знать

визуального представления этого правила, которое называется правило треугольников:

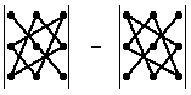
Здесь схематично показано, какие сомножители соседствуют в слагаемых.

Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца.

Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей : если оно четное «+», нечетное «-».

Инверсия - когда большее число стоит перед меньшим.

Св-ва определителей:

1. В определителе строки и столбцы равнозначны.

2. Если все Эл-ты в строке или столбце = 0, то определитель =0.

3.Обратная матрица и ее построение. Теорема существования и единственности обратной матрицы. Матричный метод решения невырожденных систем линейных алгебраических уравнений.

Матрица А наз. невырожденной,если ее определитель не равен 0

Матрица А^-1 наз. обратной к матрице А,если АА^-1= А^-1А=Е, где Е-единичная матрица. Всякая невырожденная матрица имеет единствен. обратную матрицу.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем:

Пусть дана система линейных уравнений с неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:АХ=В, где А — основная матрица системы, В и Х — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на А^-1 — матрицу, обратную к матрице А:А^-1(АХ)= А^-1В Так как А^-1А=Е, получаемХ= А^-1В. Правая часть этого уравнения даст столбец решений исходной системы

4. Ранг матрицы. Вычисление ранга матрицы методом окаймляющих миноров и с помощью элементарных преобразований.

Наибольший из порядков миноров данной матрицы отличный от нуля называется рангом матрицы.

rank A = rg A = r

Свойства ранга:

- при транспонировании матрицы ранг не меняется

- если вычеркнуть из матрицы нулевую строку, то ранг не меняется

- ранг матрицы не меняется при элементарных преобразованиях над строками матрицы.

Максимальный порядок r отличных от нуля миноров матрицы A называется ее рангом, а любой минор порядка r, отличный от нуля - базисным минором.

Основные методы вычисления ранга матрицы:

Метод окаймляющих миноров. Пусть в матрице найден минор k-го порядка M, отличный от нуля. Рассмотрим лишь те миноры (k+1)− го порядка, которые содержат в себе (окаймляют) минор M: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор (k+1)−го порядка, и вся процедура повторяется.

Метод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования матрицу можно привести к такому виду, когда все ее элементы кроме a11,a22,...,arr (r≤min(m,n)), равны нулю. Следовательно, ранг матрицы равен r.

5. ВопросСистемы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Формулы Крамера.

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

где числа a_ij называются коэффициентами системы, числа b_i— свободными членами. Подлежат нахождению числа x_n.Такую систему удобно записывать в компактной матричной формеAX=B

Здесь А — матрица коэффициентов системы, называемая основной матрицей;— вектор-столбец из неизвестных x_j.— вектор-столбец из свободных членов b_i.

Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов

Решением системы называется n значений неизвестных  х₁=c₁, x₂=c₂, ..., x_n=c_n, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записатьв виде матрицы-столбца

Система уравнений называется совместной, если она имеет хотя бы одно решение, инесовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

 Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

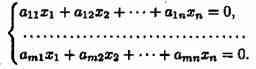
Однородная система всегда совместна, так как  x₁=x₂=x₃=...=x_n=0 является решением системы. Это решение называется нулевым или тривиальным.