Линейный двучлен. Теорема Безу.
Линейный двучлен есть многочлен первой степени: a x + b. Если разделить многочлен, содержащий букву x , на линейный двучлен x – b, где b – некоторое число (положительное или отрицательное), то остаток будет только многочленом нулевой степени, т.е. некоторым числом N , которое можно определить, не находя частного. Более точно, это число равно значению многочлена, получаемому при x = b. Это свойство вытекает из теоремы Безу: многочлен a0 xm + a1 xm-1 + a2 xm-2 + …+ am делится на двучлен x – b с остатком N = a0 bm + a1 bm-1 + a2 bm-2 + …+ am .
Д о к а з а т е л ь с т в о. В соответствии с определением операции деления многочленов имеем: a0 xm + a1 xm-1 + a2 xm-2 + …+ am = ( x – b ) Q + N ,
где Q – некоторый многочлен, N – некоторое число.
Подставим x = b , тогда слагаемое ( x – b ) Q обращается в нуль, и мы получаем:
a0 bm + a1 bm-1 + a2 bm-2 + …+ am = N .
З а м е ч а н и е . При N = 0 число b является корнем уравнения:
a0 xm + a1 xm-1 + a2 xm-2 + …+ am = 0 . Теорема доказана.
Деление многочленов
Что значит разделить один многочлен P на другой Q ? Это значит найти многочлены М (частное) и N (остаток), удовлетворяющие двум требованиям:
1) имеет место равенство: MQ + N = P ;
2) степень многочлена N меньше степени многочлена Q.
33ВОПРОСМножества и действия над ними. Элементы математической логики. Логические символы.
Множеством именуется некоторая совокупность элементов, объединенных по какому-либо признаку. Если есть такая совокупность, разумеется, как единое целое, говорят, что имеют дело с множеством. Приведенное определение не может рассматриваться как математически строгое, поскольку понятие множества является исходным, на основе него строятся остальные понятия математики. Тем не менее, из при веденного определения ясно, как можно говорить с множестве, например, действительных чисел или множестве плоских фигур. Если множество состоит из конечного числа элементов, оно называется конечным. Остальные множества называются бесконечными. Для множества используются следующие обозначения: А = {а,b,с,d}
Множество, в котором не содержится ни одного элемента, называется пустым. Обозначается оно знаком Ø.
Множества, состоящие из одних и тех же элементов, называют совпадающими. Например, совпадают два конечных множества, которые отличаются друг от друга порядком их элементов.
Определение 1. Пересечением множеств А и В называют их общую часть С. Другими словами, пересечение множеств А и В образуют элементы, принадлежащие равно как А, так и В (обозначается пересечение - n)
Определение 2. Объединением множеств А и В, называют множество С, составленное из элементов, принадлежащих хотя бы одному из этих множеств
Определение 3. Разностью множеств А и В называют множество С = В / А,
Многие
математические понятия удобно записывать
в виде выражений, содержащих некоторые
логические символы. Так, символ
,
называемыйквантором
общности,
используется вместо слов: «для
любого»,
«для всех»,
«каково бы
ни было…»
и т.д., а символ
–квантор
существования
– вместо слов «существует»,
«найдется
хотя бы один…»,
«имеется»
и т.д.
Основной объект математической логики - высказывание. Высказыванием называется повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но не как и то, и другое вместе.
Если
высказывание истинно, будем говорить,
что его значение истинности - истина
(или
(от английского true); если - ложно, то
значение истинности – ложь (
от false).
Высказывания
в математической логике обычно
обозначаются прописными латинскими
буквами:
,
,
и т.д. Для того чтобы из высказываний
получать новые высказывания, применяются
специальные операции -логические
связки.
Рассмотрим пять основных логических
связок. Сначала дадим неформальное
объяснение. Однако оно чревато
неточностями, поэтому дадим логическим
операциям также строгое определение.
Определить высказывание — значит,
указать, в каких случаях оно истинно,
а в каких ложно.
Отрицание
— это высказывание, которое получается
из данного высказывания
с помощью слова «не».
Отрицание можно обозначать по-разному:
,
,
.
Простое
добавление слова «не»
к высказыванию чаще всего будет
противоречить языковым нормам. Поэтому
в конкретных случаях требуется «перевод»
полученного высказывания на русский
язык. Пусть, например,
= «Завтра пойдет дождь». Что значит «Не
(Завтра пойдет дождь)»: «Дождь пойдет
не завтра», «Завтра пойдет не дождь»
или «Завтра не пойдет дождь»? Здравый
смысл подсказывает, что отрицанием
высказывания
является третье предложение. Чтобы
определить точно, дадим формальное
определение отрицания.
Отрицанием
высказывания
называется такое высказывание, которое
принимает значение
(ложно), если высказывание
истинно, и значение
(истинно), если высказывание
ложно.
В нашем примере этому условию удовлетворяет
только третье предложение.
Итак,
=
«Завтра
не
пойдет дождь».
Дизъюнкция
- это
высказывание, которое получается из
двух
данных
высказываний
и
спомощью
союза «или». Дизъюнкция
обозначается
.
Дизъюнкция
строится с помощью неисключающего
«или». Таким образом,
дизъюнкция
истинна,
когда истинно, по крайней мере, одно
из высказываний
и
илиоба
вместе. Другими словами,
дизъюнкция
ложна в том и только в том случае, когда
оба высказывания ложны.
Конъюнкция
- это
высказывание, которое получается из
двух данных
высказываний
и
с
помощью
союза «и». Конъюнкция обозначается
.
Конъюнкция
справедлива в том и только в том случае,
когда оба высказывания истинны.
Импликация
образуется
из высказываний
и
с помощью слов «если...
то...». Получается высказывание вида
«если
то
».
Напомним,
что математическая логика носит
формальный характер, содержанием
высказываний она не, занимается.
На
примере импликации хорошо видна разница
между обычным
языком и языком логики. В обычном языке
сложное предложение
«если
,
то
»
предполагает
между
и
отношение
посылки и
следствия, или же причины и обусловленного
ею действия.
В логике импликация связывает любые
два высказывания.
Импликация
обозначается
,
при
этом говорят: «
влечет
»
или «
при условии, что
»,
«
,
если
»,
«
есть достаточное условиедля
»,
«
есть
необходимое условие для
».
Договорились,
что импликация
ложна в том и только в том случае,
когда высказывание
истинно, а высказывание
ложно.Такое
определение подсказано здравым смыслом:
разумно считать импликацию истинной,
если
истинно,
независимо от значения
;
если оба участника импликации ложны,
импликация, естественно, также
истинна. В единственном случае, когда
«предпосылка» импликации
истинна, а «вывод» ложен, импликация
считается ложной.
Эквиваленция
образуется из высказываний
и
с помощью слов«...тогда
и только тогда, когда...»:
Утверждение
«
тогда
и только тогда, когда
»
не
означает в логике, что составляющие
высказывания
и
имеют
одно
и то же значение или один и тот же смысл.
Эквиваленция
обозначается
.
Синонимы для эквиваленции: «если
,
то
,
и если
,
то
»,
«
в том и только в том случае, когда
»,
«И есть необходимое и достаточное
условие для
»,
«
есть необходимое и достаточное условие
для
».
Разумное определение эквиваленции:
эквиваленция истинна в том и только в
том случае, когда высказывания
и
имеют одинаковое значение истинности
(либо оба истинны, либо оба ложны).
Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.
В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.
34. Необходимое и достаточное условия. Прямая и обратная теоремы.
Необходимыми условиями правильности утверждения А наз-ся такие условия, без соблюдения кот-х утверждение А заведомо не м.б. верным, а достаточными условиями правильности утверждения А наз-ся условия, при выполнении кот-х утверждение А заведомо верно. Пример: необходимым условием делимости целого числа на 2 явл-ся то, чтобы число, будучи записано в десятичной системе счисления, не кончалось цифрой 7. Условие это необходимо, но не достаточно, так как, например, число 23 не кончается цифрой 7 и всё-таки не делится на 2. Достаточным условием делимости числа на 2 явл-ся то, чтобы оно кончалось цифрой 0. Это условие достаточно, но не необходимо, так как число 38 не кончается цифрой 0 и все-таки делится на 2. Обычно употребляемый признак делимости на 2 (чтобы число делилось на 2, необходимо и достаточно, чтобы последняя его цифра делилась на 2) явл-ся примером условия одновременно необходимого и достаточного.
Обратная теорема - теорема, условием к-рой служит заключение теоремы исходной (прямой), а заключением - условие. Обратной к обр. теор. будет исходная (прямая) теорема, так что прямая и обр.т. взаимно обратны. Обр. теор. равносильна теореме, противоположной к прямой, т. е. теореме, в к-рой условие и заключение прямой теоремы заменены их отрицаниями. Поэтому прямая теорема равносильна противоположной к обратной, т. е. теореме, утверждающей, что если неверно заключение прямой теоремы, то неверно и ее условие. Известный способ "доказательства от противного" как раз и представляет собой замену доказательства прямой теоремы доказательством теоремы, противоположной к обратной. Справедливость обеих взаимно обратных теорем означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения
35ВОПРОСМетод математической индукции. Бином Ньютона.
Математическая
индукция - специальный метод доказательства
предложений типа 
(или
,
Этот метод хотя и называется индуктивным,
по своей структуре представляет собой
дедуктивное рассуждение, опирающееся
на аксиому математической индукции:
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
Где
—биномиальные
коэффициенты,n-
неотрицательное целое
число.
36ВОПРОСМножество действительных чисел. Модуль действительного числа. Ограниченные и неограниченные числовые множества. Наибольший и наименьший элементы числового множества. Верхняя и нижняя грани числового множества.
Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел(целые+рациональные(дроби)+иррациональные)
Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: | х | = - х.
Числовое множество(в конспекте-последовательность) наз. огранниченным,если существует такое число М,что все члены множества(в конспекте-последовательности) будут меньше чем М
Множество Х R наз. ограниченным сверху,если существует такое число b ∈ R, что для всех х ∈ Х имеет место неравенство х b.
Число b наз. в этом случае числом,ограничивающим сверху множество Х.
Множество Х наз. ограниченным снизу,если существует такое число а∈ R, что для всех х∈ Х выполняется неравенство х ≥ а.
Число а наз. в этом случае числом,ограничивающим снизу множество Х.
Множество,ограниченное сверху и снизу наз. ограниченным.
Множество,не являющееся ограниченным,наз. неограниченным.
Множество Х наз. неограниченным сверху,если для любого числа b∈ R найдется такой х∈ Х, что х>b.
Верхняя грань множества Е действительных чисел — наименьшее из всех чисел А, обладающих тем свойством, что для любого х из Е выполняется неравенство х ≤ А.
обозначается sup Е
Аналогично понятию Верхняя грань множества определяется нижняя грань (Н. г.) множества Е как наибольшее из чисел В, обладающих тем свойством, что для любого х из Е выполняется неравенство x ≥ B.
обозначается inf Е
Элемент а ∈ X называется наибольшим или максимальным (наименьшим или минимальным) элементом множества X R, если х ≤ а (соответственно x ≥ а) для любого элемента х ∈ X.
Если Х-числовое множество и для некоторого числа а и всех х∈ Х выполняется неравенство х ≤ а(соответственно x ≥ а),то sup ≤ а(inf х≥а), так как supХ(соответственно infХ) является наименьшим(наибольшим) среди всех чисел,ограничивающих сверху(снизу)множество Х.
37ВОПРОСПонятие предела числовой последовательности. Бесконечно малые числовые последовательности и их свойства. Свойства сходящихся последовательностей. Монотонные последовательности, теорема Вейерштрасса.
Предел числовой последовательности — предел последовательностиэлементов числового пространства. Числовое пространство — этометрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому,
предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.
Числовая последовательность — это последовательностьэлементов числового пространства.
Бесконечно малая последовательность — это последовательность, пределкоторой равеннулю.
Свойства бесконечно малых последовательностей
Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью…
Сходящаяся
последовательность —
это последовательность элементов
множества 
,
имеющаяпределв
этом множестве.
Свойства сходящихся последовательностей:
Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.
Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
Любая сходящаяся последовательность элементов хаусдорфова пространстваимеет только один предел.
Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределысовпадают.
Если
последовательность 
сходится,
но не является бесконечно малой, то,
начиная с некоторого номера, определена
последовательность
,
которая является ограниченной.
Сумма сходящихся последовательностей также является сходящейся последовательностью.
Разность сходящихся последовательностей также является сходящейся последовательностью.
Произведение сходящихся последовательностей также является сходящейся последовательностью
Любую сходящуюся
последовательность 
можно
представить в виде
,
где
—
предел последовательности
,
а
—
некоторая бесконечно малая
последовательность.
Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).
Монотонные поверхности. Теорема Вейерштрасса.
Определение. Последовательность 
не
убывает (не возрастает),
если 
для
.
Определение. Последовательность 
возрастает
(убывает),
если 
для
.
Определение. Строго возрастающая или строго убывающая последовательность называется монотонной последовательностью.
Теорема. Если 
-
не убывает и ограничена сверху, то она
сходится. Если
-
не возрастает и ограничена снизу, то
она сходится.
Доказательство. При
выполнении условия теоремы
последовательность 
ограниченна.
В силу
ограниченности 
,
1) Если
последовательность не убывает, то 
2) Если
последовательность не возрастает, то 
Рассмотрим первый случай.
По определению :
: 
Т.к. 
не
убывает, то при
при 
при 
.
Второй случай рассматривается аналогично.
38ВОПРОСПонятие функции. Предел функции в точке и на бесконечности. Односторонние пределы. Свойства функций, имеющих предел.
|
Пусть задано числовое множество
|
Если
каждому числу 
поставлено
в соответствие единственное числоy,
то говорят, что на множестве D задана
числоваяфункция: y = f (x), 
Множество D называется областью
определения функции и
обозначается D (f (x)).
Множество, состоящее из всех
элементов f (x),
где 
называетсяобластью
значений функции и
обозначается E (f (x)).
Число x часто
называют аргументом
функции или
независимой переменной, а число y –
зависимой переменной или,
собственно, функцией переменной x.
Число
соответствующее значению
называютзначением
функции в
точке 
и
обозначают
или
Преде́л
фу́нкции —
одно из основных понятий математического
анализа.
Функция 
имеет
предел
в
точке
если
для всех значений
,
достаточно близких к
,
значение
близко
к
.
Односторонние пределы
Односторонние пределы
Пусть
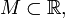и
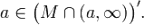Тогда
система множеств
является фильтром
и обозначается 
или
Предел
называется
правосторонним пределом
функции
при
стремящемся
к
Пусть
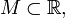и
Тогда
система множеств
является фильтром
и обозначается 
или
Предел
называется
левосторонним пределом
функции
при
стремящемся
к
Пределы на бесконечности
Пусть
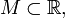и
Тогда
система множеств
называется
пределом функции 
при
стремящемся
к бесконечности.
Пусть
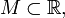и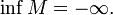
Тогда
система множеств
является фильтром
и обозначается 
Предел
называется
пределом функции
при
стремящемся
к минус-бесконечности.
Свойства пределов функции
1) Предел постоянной величины
Предел
постоянной величины равен самой
постоянной величине:
2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы:
Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:
Расширенное свойство предела произведения
Предел произведения нескольких функций равен произведению пределов этих функций:
5) Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций. Эквивалентные функции и их применение к вычислению пределов
Бесконечно большая функция (б.б.ф)
Функция y
= f
(x)
называется бесконечно большой при х→
х0,
если для любого числа М > 0 существует
число δ = δ (М) > 0, что для всех х,
удовлетворяющих неравенству 0 < |х-
х0|
< δ, выполняется неравенство |f(х)|
> М. Записывают
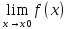= ∞ илиf
(x)
→ ∞ при х → х0.
Если f(х)
стремится к бесконечности при х → х0
и принимает лишь положительные значения,
то пишут
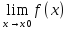= + ∞; если лишь отрицательные значения,
то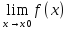
= - ∞.
Бесконечно малая функция (б.м.ф.)
Функция у = f(x)
называется бесконечно малой при х→
х0,
если
.
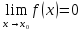По определению предела функции равенство
означает: для любого числаɛ
> 0 найдется число δ > 0 такое, что
для всех х, удовлетворяющих неравенству
0 < |х – х0|
< δ, выполняется неравенство |f
(x)|
< ɛ.
Аналогично определяется б.м.ф. при х→ х0 + 0, х→ х0 – 0, х→ + ∞, х→ - ∞: во всех этих случаях f (x) →0.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, β и т.д.
Сравнение бесконечно малых функций
Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Две б.м.ф.сравниваются между собой с помощью их отношения.
Пусть α = α(х) и β =
β(х) есть б.м.ф. при х → х0,
т.е.
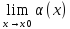= 0 и
= 0.
1.если
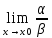= А ≠ 0 (А €R),
то α и β называются бесконечно малыми
одного порядка.
2.если
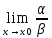= 0, то α называется бесконечно малой
более высокого порядка, чем β.
3если
= ∞, то α называется бесконечно малой
более низкого порядка, чем β.
4.если
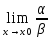не существует, то α и β называются
несравнимыми бесконечно малыми.
Отметим, что такое же правило сравнения б.м.ф.при х → ± ∞, х → х0 ± 0.
Эквивалентные функции
Среди бесконечно малых функций одного порядка особую роль играют так назывемые эквивалентные бесконечно малые.
Если
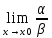= 1, то α и β называются эквивалентными
бесконечно малыми (при х → х0);
это обозначается так: α ~ β.
Применение эквивалентных функций для вычисления пределов
Для раскрытия
неопределенностей вида
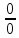часто бывают полезным применять принцип
замены бесконечно малых эквивалентными
и другие свойства эквивалентных
бесконечно малых функций. Как известно,sin
x
~ х при х → 0, tg
х ~ х при х → 0.
важнейшие эквивалентности, которые используют для вычисления пределов:
sin х ~ х при х → 0;
tg х ~ х (х → 0);
arcsin х ~ х (х → 0);
arctg х ~ х (х → 0);
1 – cos х ~
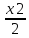(х → 0);
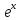- 1 ~ х (х → 0);
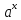- 1 ~ х * ln
а (х → 0);ln (1+х) ~ х (х → 0);
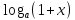~ х *
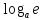(х → 0);(1 + х)k – 1 ~ k * х, k > 0 (х → 0);
в частности,
- 1 ~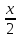
.
40ВОПРОС Непрерывность функции в точке и на отрезке. Свойства функций, непрерывных в точке.
Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Тот
же факт можно записать иначе:
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
Свойства функций, непрерывных в точке
Поскольку
точки 
непрерывно
сти
функции
задаются
условием
,
то часть свойств функций, непрерывных
в точке
,
следует непосредственно из свойств
пределов. Сформулируем их в виде
следующей теоремы.
Теорема 3.1 Пусть
функции 
и
непрерывны
в точке
.
Тогда функции
,
,
непрерывны
в точке
.
Если
,
то функция
также
непрерывна в точке
.
Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение 3.3 Рассмотрим
множество всех функций, определённых
в некоторой фиксированной
окрестности 
точки
и
непрерывных в этой точке. Тогда это
множество
является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
Доказательство.
Действительно, постоянные 
и
--
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке
пpоизведения
и
.
Но тогда по этой же теоpеме непpеpывна
в точке
и
сумма
.
Теорема 3.2 Пусть
функции 
и
таковы,
что существует композиция
,
.
Пусть функция
непрерывна
в точке
,
а функция
непрерывна
в соответствующей точке
.
Тогда композиция
непрерывна
в точке
.
Доказательство.
Заметим, что равенство 
означает,
что при
будет
.
Значит,
(последнее
равенство следует из непрерывности
функции 
в
точке
).
Значит,
а
это равенство означает, что
композиция 
непрерывна
в точке
.
Заметим,
что, очевидно, в предыдущих двух теоремах
можно было бы заменить базу 
на
односторонние базы
или
и
получить аналогичные утверждения для
непрерывности слева или справа:
Теорема 3.3 Пусть
функции 
и
непрерывны
слева (справа) в точке
.
Тогда функции
,
,
непрерывны
слева (соотв. справа) в точке
.
Если
,
то функция
также
непрерывна слева (спpава) в точке
.
Теорема 3.4 Пусть
функция 
непрерывна
слева (справа) в точке
,
а функция
непрерывна
в точке
.
Тогда композиция
непрерывна
слева (соотв. справа) в точке
.
41ВОПРОС Точки разрыва функции и их классификация. Непрерывность элементарных функций.
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
-
Существуют левосторонний предел 
и
правосторонний предел
;
-Эти односторонние пределы конечны.
При этом возможно следующие два случая:
-Левосторонний предел и правосторонний предел равны друг другу:
Такая
точка называется точкой
устранимого разрыва.
-Левосторонний
предел и правосторонний предел не равны
друг другу:
Такая
точка называетсяточкой
конечного разрыва.
Модуль
разности значений односторонних
пределов
называетсяскачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Непрерывность элементарных функций
Целая
и дробная рациональные
функции. Непрерывность f(x)=const и f(x)=x непосредственно
ясна. На основании теоремы о произведении
непрерывных функций вытекает непрерывность
любого одночленного выражения axm,
по теореме о сумме непрерывных функций
- непрерывность многочлена a0xn +
a1xn-1 +
... +an-1 +
an.
Непрерывность данных функций имеет
место на всем интервале 
.
Частное двух многочленов
непрерывно
всюду, кроме точекb0xm +
b1xm-1 +...+
bm-1x
+ bm =
0 (в
этих точках - либо разрыв 2-го рода, либо
устранимый разрыв).
Показательная
функция y=ax(a>1) монотонно
возрастает на всем интервале 
.
Ее значения заполняют весь интервал
.
Из существования логарифма следует
непрерывность данной функции.
Логарифмическая
функция 
.
Рассмотрим случайa>1.
Эта функция возрастает при 
,
и принимает любое значение из
.
Отсюда следует ее непрерывность.
Степенная
функция 
.
При возрастанииx от
0 до 
возрастает
или
убывает
на
интервале
.
Следовательно, данная функция непрерывна.
Тригонометрические
функции 
,
,
,
,
,
.
Остановимся на функции
.
Ее непрерывность на отрезке
вытекает
из ее монотонности, а также из факта
(устанавливаемого геометрически), что
при этом она принимает все значения от
-1 до 1. То же относится к любому
промежутку
.
Следовательно, функция
непрерывна
для всех значенийx.
Аналогично - для функции 
.
По свойствам непрерывных функций
вытекает непрерывность функций
.
Исключение для первых двух функций -
значенияx вида 
,
при которых
,
для других двух - значения вида
,
при которых
.
Обратные
тригонометрические функции 
,
,
,
.
Первые две непрерывны на
,
остальные - на