
- •2. Определители 2 и 3-го порядков. Вычисление определителя n-го порядка. Свойства определителей 3-го порядка.
- •3.Обратная матрица и ее построение. Теорема существования и единственности обратной матрицы. Матричный метод решения невырожденных систем линейных алгебраических уравнений.
- •4. Ранг матрицы. Вычисление ранга матрицы методом окаймляющих миноров и с помощью элементарных преобразований.
- •4.2. Решение систем линейных уравнений.
- •4.3 Решение невырожденных линейных систем. Формулы Крамера
- •7 Вопрос Системы линейных однородных уравнений
- •6Вопрос Решение систем линейных уравнений методом Гаусса
- •8 Вопрос Декартова система координат. Понятие вектора. Линейные операции над векторами. Координаты вектора. Линейная зависимость и независимость векторов. Понятие базиса.
- •5.2. Линейные операции над векторами
- •Линейная зависимость и независимость векторов
- •20. Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью.
- •Эллипсоид
- •Однополостный гиперболоид
- •Двуполостный гиперболоид
- •Гиперболический параболоид
- •Эллиптический цилиндр
- •Гиперболический цилиндр
- •Параболический цилиндр
- •22 Вопрос Эллипсоид.
- •24. Параболоиды.
- •26. Евклидово пространство. Неравенство Буняковского-Коши. Ортогональный и ортонормированный базисы. Разложение вектора по ортогональному базису.
- •Вопрос 27 Линейные операторы. Матрица линейного оператора. Действия над линейными операторами. Зависимость между матрицами линейного оператора в различных базисах.
- •Применение квадратичных форм к исследованию кривых второго прядка
- •Линейный двучлен. Теорема Безу.
- •Деление многочленов
- •42.Замечательные пределы.
- •Вопрос 43
- •1. Теорема Ролля
- •2. Теорема Лагранжа
- •3. Теорема Коши
- •4. Правило Лопиталя
- •Геометрический смысл производной
- •Механический смысл производной
Геометрический смысл производной
Пусть
функция ![]() определена
в некоторой окрестности
определена
в некоторой окрестности![]() токи
токи![]() ,
непрерывна в этой точке и
,
непрерывна в этой точке и![]() ,
а
,
а![]()
Придав
произвольное приращение аргументу ![]() ,
так
,
так![]() чтобы ,
перейдем к точке
чтобы ,
перейдем к точке![]() с
абсциссой
с
абсциссой![]() и
ординатой
и
ординатой![]() ,
где
,
где![]() .
.
Уравнение
прямой, проходящей через точки ![]() и
и![]() (секущей
графика функции
(секущей
графика функции![]() ,
имеет вид:
,
имеет вид:![]() ,
где отношение
,
где отношение![]() представляет
собой угловой коэффициент секущей (
представляет
собой угловой коэффициент секущей (![]() .
.
Касательной
к графику функции ![]() в
точке
в
точке![]() называется
предельное положение секущей
называется
предельное положение секущей![]() ,
при стремлении точки
,
при стремлении точки![]() по
графику
по
графику![]() к
точке
к
точке![]() .
.
Для
того, чтобы секущая ![]() при
при![]() стремилась
к предельному положению, отличному от
вертикальной прямой , необходимо и
достаточно, чтобы существовал конечный
предел
стремилась
к предельному положению, отличному от
вертикальной прямой , необходимо и
достаточно, чтобы существовал конечный
предел![]() ,
то есть , чтобы существовала конечная
производная функции
,
то есть , чтобы существовала конечная
производная функции![]() в
точке
в
точке![]() .Угловой
коэффициент касательной получается
путем перехода от
.Угловой
коэффициент касательной получается
путем перехода от![]() к
пределу при
к
пределу при![]() :
:![]()
Таким
образом, получим, что ![]() ,
где
,
где![]() -
угол наклона касательной к оси
-
угол наклона касательной к оси![]() (см.
рис.), а значение производной равно
угловому коэффициенту касательной к
графику функции. В этом
заключаетсягеометрический
смысл производной.
(см.
рис.), а значение производной равно
угловому коэффициенту касательной к
графику функции. В этом
заключаетсягеометрический
смысл производной.
Механический смысл производной
Пусть
материальная точка движется прямолинейно
и ![]() -
длина пути, проходимого за время
-
длина пути, проходимого за время![]() ,
отсчитываемого от некоторого момента
времени
,
отсчитываемого от некоторого момента
времени![]() .
.
Для
определения скорости ![]() в
данный момент
в
данный момент![]() придадим
переменной
придадим
переменной![]() некоторое
приращение
некоторое
приращение![]() ,
при этом приращение пути будет равно
,
при этом приращение пути будет равно![]() .
.
Отношение ![]() называется
в физике величиной средней скорости
движения за промежуток времени, начиная
с момента времени
называется
в физике величиной средней скорости
движения за промежуток времени, начиная
с момента времени![]() ,
и обозначается
,
и обозначается![]()
Предел ![]() называется
величиной мгновенной скорости движения
в момент времени
называется
величиной мгновенной скорости движения
в момент времени![]() .
.
Таким
образом, мгновенная скорость в момент
времени ![]() прямолинейного
движения, совершаемого по закону
прямолинейного
движения, совершаемого по закону![]() равна
значению производной
равна
значению производной![]() .
.
56 ВОПРОСКасательная прямая и нормальная плоскость к пространственной кривой. Кривизна и кручение пространственной кривой. Формулы Френе.
Соприкасающаяся плоскость и нормали
Если
взять в качестве ![]() плоскость,
проходящую через точку
плоскость,
проходящую через точку![]() кривой
кривой![]() ,
то условие соприкосновения
при
,
то условие соприкосновения
при![]() определяетсоприкасающуюся
плоскость кривой
(рис. 1). Дважды дифференцируемая кривая
в каждой точке имеет соприкасающуюся
плоскость. Она либо единственная, либо
любая плоскость, проходящая через
касательную кривой, является
соприкасающейся.
определяетсоприкасающуюся
плоскость кривой
(рис. 1). Дважды дифференцируемая кривая
в каждой точке имеет соприкасающуюся
плоскость. Она либо единственная, либо
любая плоскость, проходящая через
касательную кривой, является
соприкасающейся.
Пусть ![]() —
уравнение кривой. Тогда уравнение
—
уравнение кривой. Тогда уравнение![]() её
соприкасающейся плоскости определяется
из соотношения:
её
соприкасающейся плоскости определяется
из соотношения:
![]()
В координатах оно имеет вид:
![]()
Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Также нормалью и бинормалью для краткости могут называть единичные векторы вдоль этих прямых (при этом направление вектора главной нормали обычно выбирают совпадающим с направлением вектора кривизны кривой[1]).
Векторное
уравнение бинормали в точке, отвечающей
значению ![]() параметра
параметра![]() ,
имеет вид:
,
имеет вид:![]()
Направление
главной нормали может быть получено
как двойное векторное
произведение: ![]() .
.
Для
плоской кривой содержащая её плоскость
совпадает с соприкасающейся. Нормаль,
с точностью до знака, только одна —
главная, и её уравнение в точке ![]() имеет
следующий вид.
имеет
следующий вид.
Параметрическое
задание: ![]()
Явное задание:
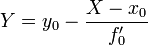
Неявное задание:
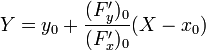
Кривизна
При движении вдоль кривой её касательная меняет направление. Скорость этого вращения (отношение угла поворота касательной за бесконечно малый промежуток времени к этому промежутку) при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. Производная же по времени положительного единичного вектора касательной называется в этом случае вектором кривизны кривой. То и другое - функции точки кривой. Кривизна есть абсолютная величина вектора кривизны.
В случае произвольного параметрического задания кривой[2] кривизна кривой в трехмерном пространстве определяется по формуле
![]() ,где
,где ![]() —
вектор-функция с координатами
—
вектор-функция с координатами![]() .
.
В координатах:
![]()
Для кривой в более многомерном пространстве можно заменить векторное произведение, обозначенное здесь квадратными скобками, на внешнее произведение.
Также для кривой в пространстве любой размерности можно воспользоваться формулой вектора кривизны:
![]()
и фактом, что кривизна есть его модуль, а также выражением для единичного вектора касательной
![]() и
и![]()
и получить для кривизны формулу:
![]() или,
раскрыв скобки:
или,
раскрыв скобки:![]()
Прямые и только прямые имеют всюду равную нулю кривизну. Поэтому кривизна наглядно показывает, насколько (в данной точке) кривая отличается от прямой линии: чем ближе кривизна к нулю, тем это отличие меньше. Кривизна окружности радиуса R равна 1/R.
Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость.
Для
плоских кривых можно различать
направление вращения касательной при
движении вдоль кривой, поэтому кривизне
можно приписывать знак в зависимости
от направления этого вращения. Кривизна
плоской кривой, задаваемой уравнениями ![]() ,
определяется по формуле
,
определяется по формуле
![]() .
.
Знак ![]() или - берётся
по соглашению, но сохраняется вдоль
всей кривой.
или - берётся
по соглашению, но сохраняется вдоль
всей кривой.
]Кручение
При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная к кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения.
Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определённое кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле
![]() здесь
здесь ![]() обозначаетсмешанное
произведение.
В координатах для натуральной
параметризации:
обозначаетсмешанное
произведение.
В координатах для натуральной
параметризации:
![]()
Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская.
ФОРМУЛЫ ФРЕНЕ.
Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе,). Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей.
Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой:
![]()
где ![]() и
и![]() —
кривизна и кручение кривой в указанной
точке.
—
кривизна и кручение кривой в указанной
точке.
Единичные
векторы ![]() ,
соответственно для касательной, главной
нормали и бинормали кривой, при движении
вдоль кривой изменяются. При соответствующем
выборе направления этих векторов из
определения кривизны и кручения
получаются формулы:
,
соответственно для касательной, главной
нормали и бинормали кривой, при движении
вдоль кривой изменяются. При соответствующем
выборе направления этих векторов из
определения кривизны и кручения
получаются формулы:
|
|
|
|
|
|
|
|
