Вопрос 27 Линейные операторы. Матрица линейного оператора. Действия над линейными операторами. Зависимость между матрицами линейного оператора в различных базисах.

пусть заданы линейные пространства X и Y. Правило, по которому  каждому элементу x e X ставится в соответствие единственный элемент y e Y , называется оператором, действующим в линейных пространствах X , Y. Результат  действия оператора A на элемент x обозначают y = A x или  y = A(x).  Если элементы x и y связаны соотношением y = A x, то y называют образом элемента x; элемент x прообразом элемента y.

Множество элементов линейного пространства X, для которых определено действие оператора A, называют областью определения оператора и обозначают D(A).

Множество элементов линейного пространства Y, которые являются образами элементов из области определения  оператора A, называют образом оператора и обозначают Im(A). Если y = A x  , то x e D(A), y e Im(A) .

Оператор A, действующий в линейных пространствах X , Y называется линейным оператором, если

A(u+v)=A(u)+A(v) и A(au)=aA(u)  и  для любых u,v e X  и для любого числа a.

Если пространства X и Y совпадают, то говорят, что оператор действует в пространстве X. В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве X.

Линейный оператор и его матрица. Переход к другому базису

Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X, dim(x)=n  и пусть e₁,  e₂, ..., e_n - базис в X. Обозначим через A e₁ = (a₁₁,...,a_n1), ... , A e_n = (a_1n,...,a_nn) образы базисных векторов e₁,  e₂, ..., e_n .

Матрица

столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно - каждая  квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения

с одной стороны, связывают координаты образа y = A x с координатами прообраза X, с другой стороны,  описывают действие оператора, заданного матрицей A.

При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве X произошел переход от базиса e = {e₁, ... , e_n}  к базису e' = {e'₁, ... , e'_n} . Связь между матрицей A_e  оператора A в базисе e  и матрицей A_e'  этого оператора в базисе e' задается формулой 

Здесь  -  матрица перехода от базиса e к базису  e' и обратная к ней.

Сложение линейных операторов обладает, очевидно, следующими свойствами:

1. А + В = В +А.

2. (А +В) +Е = А + (В + Е).

3. А + О = А  для любого А.

4. (–А) + А = О.

Справедливы следующие свойства умножения линейных операторов:

1. АВ) = (А )В.

2. (АВ)Е = А (ВЕ).

3. (А + В)Е = АЕ + ВЕ,  Е(А + В) = ЕА + ЕВ.

Для умножения линейного оператора на число справедливы, очевидно, следующие свойства:1. А = А; 0А = О; (–1)А= –А. 2.βА) А.3.А =А +βА. 4. (А + В) =А +В.

28ВОПРОС Собственные векторы и собственные значения матриц и их свойства. Характеристическое уравнение и многочлен матрицы. Приведение матрицы к диагональному виду.

Будем говорить, что на множестве векторов R задано преобразование А, если каждому вектору хR по некоторому правилу поставлен в соответствие вектор АхR. 

Определение 9.1. Преобразование А называется линейным, если для любых векторов х и у и для любого действительного числа λ выполняются равенства:

               А(х + у)=Ах + Ау,   А(λх) = λ Ах.                                                           (9.1) 

Определение 9.2.  Линейное преобразование называется тождественным, если оно преобразует любой вектор х в самого себя.  

Тождественное преобразование обозначается Е:  Ех = х.

   Рассмотрим трехмерное пространство с базисом е₁, е₂, е₃, в котором задано линейное преобразование А. Применив его к базисным векторам, мы получим векторы Ае₁, Ае₂, Ае₃, принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса:

                    Ае₁ = а₁₁ е₁ + а₂₁ е₂ +а₃₁ е₃,

                    Ае₂ = а₁₂ е₁ + а₂₂ е₂ + а₃₂ е₃,                                                                     (9.2)

                    Ае₃ = а₁₃е₁ + а₂₃ е₂ + а₃₃ е₃    .

Матрица     называется матрицей линейного преобразования А в базисе е₁, е₂, е_3 . Столбцы этой матрицы составлены из коэффициентов в формулах (9.2) преобразования базиса. 

Замечание. Очевидно, что матрицей тождественного преобразования является единичная матрица Е. 

  Для произвольного вектора х =х₁е₁ + х₂е₂ + х₃е₃ результатом применения к нему линейного преобразования А будет вектор Ах, который можно разложить по векторам того же базиса: Ах =х`<sub>1</sub>е<sub>1</sub> + х`₂е₂ + х`<sub>3</sub>е<sub>3</sub>, где координаты x`_i можно найти по формулам:

        х`₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃,

        x`₂ = a₂₁x₁ + a₂₂x₂ + a₂₃x₃,                                                                                     (9.3)

        x`₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃.

Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.

                         Преобразование матрицы линейного преобразования при переходе к новому базису. 

   Рассмотрим линейное преобразование А и два базиса в трехмерном пространстве: е₁, е₂, е₃ и е₁, е₂, е_3.  Пусть матрица С задает формулы перехода от базиса {e_k} к базису {e_k}. Если в первом из этих базисов выбранное линейное преобразование задается матрицей А, а во втором – матрицей А, то можно найти связь между этими матрицами, а именно:

                                        А = С^-1АС                                                                (9.4)

Действительно,  , тогда А. С другой стороны, результаты применения одного и того же линейного преобразования А в базисе {e_k}, т.е. , и в базисе {e_k}: соответственно  - связаны матрицей С: , откуда следует, что СА=АС. Умножая обе части этого равенства слева на С^-1, получим  С^-1СА  = = С^-1АС, что доказывает справедливость формулы (9.4). 

               Собственные числа и собственные векторы матрицы. 

Определение 9.3. Вектор х называется собственным вектором  матрицы А, если найдется такое число λ, что выполняется равенство: Ах = λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называется собственным числом  матрицы А.

  Подставив в формулы (9.3)  x`_j = λx_j, получим систему уравнений для определения координат собственного вектора:

    .

Отсюда

                                          .                                (9.5)

Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

                             

получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:

                            | A -  λE | = 0,                                                                            (9.6)

поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ   | A -  λE| называется характеристическим многочленом  матрицы А. 

                   Свойства характеристического многочлена:

1)       Характеристический многочлен линейного преобразования не зависит от выбора базиса.                                                                                                           Доказательство. (см. (9.4)), но  следовательно, . Таким образом,  не зависит от выбора базиса. Значит, и |A-λE| не изменяется при переходе к новому базису.

2)       Если матрица А линейного преобразования является симметрической (т.е. а_ij=a_ji), то все корни характеристического уравнения (9.6) – действительные числа. 

              Свойства собственных чисел и собственных векторов:

1)        Если выбрать базис из собственных векторов х₁, х₂, х₃, соответствующих собственным значениям  λ₁, λ₂, λ₃ матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

                                                                                    (9.7)                                                    Доказательство этого свойства следует из определения собственных векторов.

2)        Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.

3)        Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

29ВОПРОСКвадратичные формы и их матрицы. Приведение квадратичной формы к каноническому виду ортогональным преобразованием. Знакоопределённые квадратичные формы. Условия знакоопределённости квадратичных форм.

Квадратичной формой /(хих2,...,х„) п действительных переменных х1,х2,...,х„ называется сумма вида

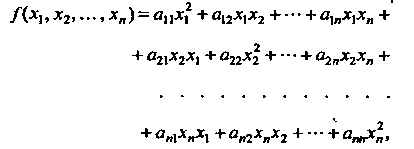
Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты соответственно действительными или комплексными числами. Будем рассматривать действительные квадратичные формы.

Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (11.1) соответствует единственная симметрическая матрица

(11.3)

И наоборот, всякой симметрической матрице (11.3) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма п переменных называется невырожденной, если ее матрица невырожденная, т. е. г = п, и вырожденной, если г < п.

Квадратичную форму (11.1) п переменных хх, х2, ...,х„ можно записать в матричном вцце. Действительно, если X - матрица-столбец из переменных

- матрица, полученная транспонированием матрицыТ. е. матрица-строка из тех же переменных, то

(11.4)

Где А определяется формулой (11.3).

Ортогональное преобразование. Для того чтобы привести квадратич­ную форму f(x_l,x₂,x₃) к каноническому виду (10.4), необходимо выписать матрицу квадратичной формы

у которой A_ij = A_ji т. е. элементы, симметричные относительно главной диа­гонали, совпадают. Затем составляем и решаем характеристическое уравне­ние:

Так как матрица симметричная, то корни λ₁,λ₂,λ₃ характеристического уравнения являются действительные числа. Найденные собственные числа являются коэффициентами в каноническом виде квадратичной формы в ба­зисе е'₁,е'₂, е'₃:

f(x'₁,x'₂, x'₃)= f₁x'²₁ + f₂x'²₂ + f₃x'²₃

Пусть найдены нормированные собственные векторы, соответствую­щие характеристическим числам γ ₁ γ ₂, γ₃ в ортонормированном базисе е₁ е₂, е₃:

е'₁ = q₁₁ е₁+ q₂₁ е₂ + q₃₁ е₃ ,

е'₂ = q₁₂ е₁+ q₂₂ е₂ + q₃₂ е₃ ,

е'₃ = q₁₃ е₁+ q₂₃ е₂ + q₃₃ е₃ ,

В свою очередь, векторы е'_ь е'₂, е'з образуют ортонормированный базис. Матрица

является матрицей перехода от базиса e₁, е₂, е₃ к базису е'₁,е'₂, е'₃

Формулы преобразования координат при переходе к новому ортонор-мированному базису имеют вид:

Принято говорить, что квадратичная форма f(x_l,x₂,x₃) приведена к каноническому виду с помощью ортогонального преобразования В.

Метод Лагранжа выделения полных квадратов. Пусть дана квадра­тичная форма (Ю.З) и пусть все коэффициенты a_ij (при квадратах х_i²), i=1,2,3. равны нулю и в тоже время форма не равна тождественно нулю, то отлично от нуля хотя бы одно произведение, например 2a_l2x₁x₂ , т. е.

f(x_l,x₂,x₃)= 2a_l2x₁x₂

Выполним преобразование базиса, при котором координаты векторов в старом и новом базисах связаны формулами:

x₁= x'₁ - x'₂

x₂= x'₁ + x'₂

x₃= x'₃

Тогда   f(x_l,x₂,x₃)-2a_l2x₁x₂.= 2a₁₂( х'₁² - х'₂²)=2а₁₂х'₁² -2а₁₂х'₂²,   и   так как, по предположению,а₁₁ = а₂₂ =0, то коэффициент при х'₁² отличен от

нуля.

Таким образом, всегда найдется такой базис, в котором в квадратичной форме хотя бы один коэффициент при квадрате отличен от нуля.

Действительная квадратичная форма /(х,, х2,  называется положитель

Но-определенной, если она приводится к нормальному виду, состоящему из л положительных квадратов: /(х],х2,...,х„)~у(у1,у2,...,у„), где

Ч>(.У1,У2,-,У„) = У?+у1+-+У*,  (Н.9)

Т. е. если ранг и положительный индекс инерции равны числу неизвестных.

Систему значений хих2,...,хП назовем нулевой, если хх=х2=...= = х„ = О, и ненулевой, если хотя бы одно из них отлично от нуля.

Т ео рем а 11.6. Действительная квадратичная форма /(*,, *2,..., х„) является положительно-определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений переменных

*1> Х2у... , Хп.

Пусть дана квадратичная форма /(хи х2,... ,хп) с матрицей А = (ац). Главными минорами квадратичной формы/называются миноры

Т. е. миноры порядкаМатрицы, расположенные в левом верхнем углу;

Последний из них совпадает с определителем матрицы.

Теорема 11.7. Квадратичная формаС действительной

Матрицей является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны.

Действительная квадратичная форма называется отрицательно-определенной, если она является невырожденной и приводится к нормальному виду, содержащему только отрицательные квадраты всех переменных; эту форму можно привести к виду

(11.10)

Теорема 11.8. Квадратичная форма является отрицательно-определенной тогда и только тогда, когда ее главные миноры четного порядка положительны, а нечетного — отрицательны.

Положительно-определенные и отрицательно-определенные квадратичные формы называются знакоопределенными квадратичными формами.

Вырожденные квадратичные формы, нормальный ввд которых состоит из квадратов одного знака, называются полуопределенными.

Неопределенными называются квадратичные формы, нормальный вид которых содержит как положительные, так и отрицательные квадраты переменных.

30 ВОПРОС Применение квадратичных форм к исследованию кривых и поверхностей второго порядка.

Квадратичной формой отнеизвестныхназывается сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.