
Математика для инженеров(теория)I том
.pdf

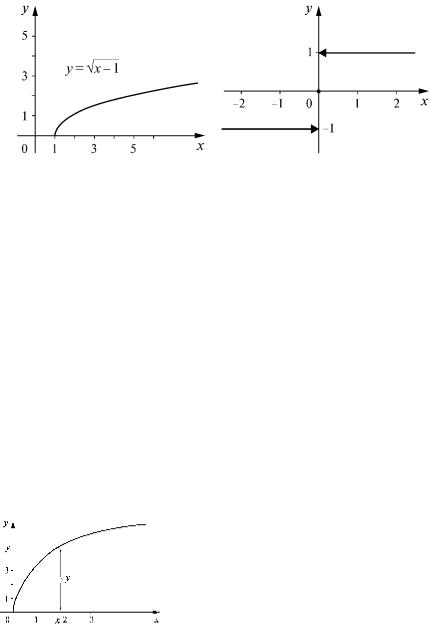
Рис. 1 а) Рис. 1 б)
2) Табличный способ. Предположим, что нас интересует зависи- мость расхода топлива от скорости движения легкового автомобиля опре- деленной марки. В инструкции к автомобилю имеется следующая таблица:
Скорость движения (км/час) |
70 |
80 |
90 |
100 |
110 |
120 |
|
|
|
|
|
|
|
Расход топлива (л) |
6,6 |
6,3 |
6,1 |
6,4 |
7,0 |
8,0 |
|
|
|
|
|
|
|
Из таблицы видно, что расход топлива изменяется в зависимости от скорости движения автомобиля и, если каждому значению скорости, записанному в первой строке таблицы, поставить в соответствие число литров топлива, стоящих во второй строке и в этом столбце, то получим функцию, заданную таблично. Областью определения этой функции является множество из 6 чисел, стоящих в первой строке. Множеством значений является также совокупность из 6 чисел второй строки.
С помощью таблицы часто задают функции, значения которых вычислить сложно. Например, широко известны таблицы тригономет- рических функций, показательной и логарифмической функций и т.д.
3) Графический способ. В данном случае предполагается, что задан график функции y = f (x) (рис. 2).
|
Здесь, чтобы для некоторого значе- |
|
ния аргумента x найти соответствующее |
|
значение функции, нужно построить на оси |
|
Ох точку х, затем восстановить в этой точке |
|
перпендикуляр к оси Ох, найти точку пере- |
|
сечения этого перпендикуляра с графиком |
|
и найти длину этого перпендикуляра. |
Рис. 2 |
Значение функции будет равно этому числу |
с соответствующим знаком. |
Примерами графического изображения могут быть записи самопишущих приборов (барографы, осциллографы и т.д.).
236
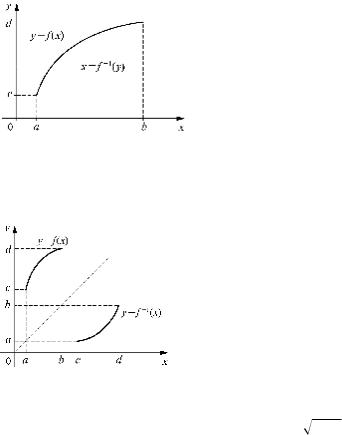

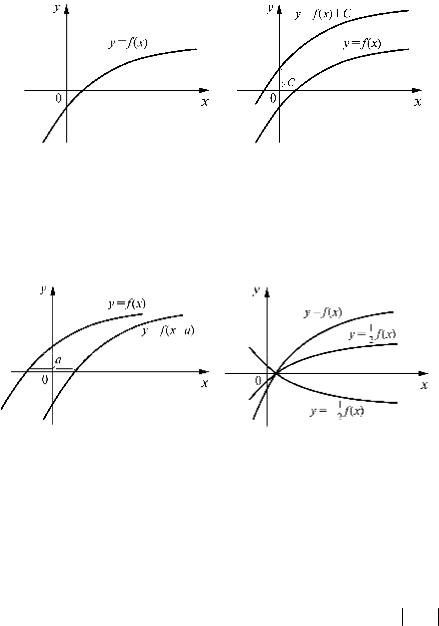
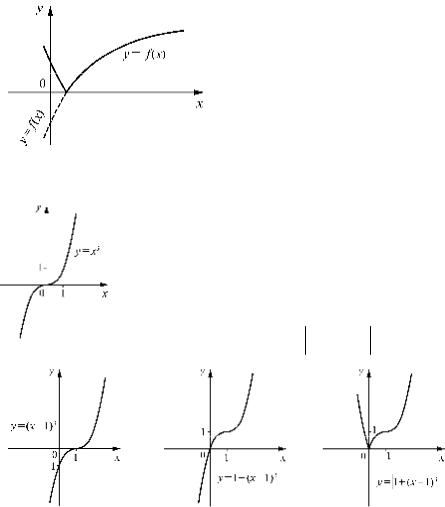

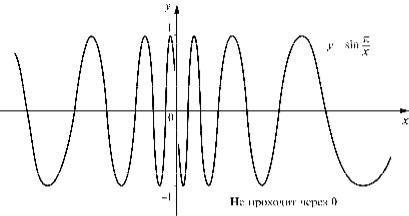
Рис. 1
Упражнение 1. Доказать эквивалентность двух приведенных определений предела функции.
20. Односторонние пределы. В определении предела функции
lim f (x) = b считается, что х стремится к а любым способом: оставаясь
x→a
меньше, чем а (слева от а) или больше, чем а (справа от а).
Бывают случаи, когда способ приближения аргумента х к а существенно влияет на значение предела функции. Поэтому вводят понятие односторонних пределов.
Число b называется правым пределом (пределом справа) в точке x = a , если для любой сходящейся к а последовательности { xn} , члены которой больше или равны а ( "nÎ : xn ³ a ), соответствующая
последовательность { f (xn )} сходится к b; обозначается: |
lim |
f (x) = b . |
||||
|
|
|
|
|
x→a+0 |
|
|
Аналогично, число b называется левым пределом (слева) в точке |
|||||
x = a , если "{ x } |
lim x |
= a , |
"nÎ : x £ a , соответствующая по- |
|||
|
n |
n→∞ n |
|
n |
|
|
следовательность { f (xn )} |
сходится к b; обозначается: |
lim |
f (x) = b . |
|||
|
|
|
|
|
x→a−0 |
|
|
Естественно, что можно сформулировать эти определения |
|||||
«на языке ε − δ ». |
|
|
|
|
|
|
|
Правый и левый пределы функций в точке называются одно- |
|||||
сторонними. В случае, |
когда |
a = 0 , используются |
обозначения: |
|||
lim |
f (x) , lim f (x) . |
|
|
|
|
|
x→+0 |
x→−0 |
|
|
|
|
|
|
Коротко предел слева и справа обозначают f (a - 0), |
f (a + 0) . |
||||
|
242 |
|
|
|
|
|





 Если же условиться и в случае функции
Если же условиться и в случае функции 
