
Математика для инженеров(теория)I том
.pdf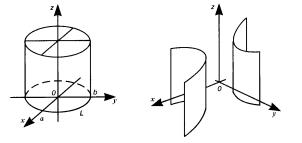
|
x2 |
+ |
|
y2 |
=1, |
(2) |
|
a2 |
|
b2 |
|||
|
|
|
|
|
||
гиперболический цилиндр |
|
|
|
|
|
|
|
x2 |
− |
|
y2 |
=1, |
(3) |
|
a2 |
|
b2 |
|||
|
|
|
|
|
||
параболический цилиндр |
|
|
|
|
|
|
|
y2 = 2 px . |
(4) |
||||
Образующие всех трех цилиндров, определяемых уравнениями (2), (3), (4), параллельны оси Oz, а направляющей служит соответст- вующая кривая второго порядка (эллипс, гипербола, парабола), лежащая в плоскости Oxy.
Отметим, что кривую в пространстве можно задать либо параметрически, либо в виде линии пересечения двух поверхностей. Например, уравнения направляющей эллиптического цилиндра, т.е. уравнения эллипса в плоскости Oxy, имеют вид
|
x2 |
+ |
y2 |
=1, z = 0 . |
|
a2 |
b2 |
||
|
|
|
||
Пример 3. Определить, какую поверхность в пространстве задает |
||||
уравнение x2 = 4y . |
|
|
|
|
Решение. Уравнение x2 = 4y |
определяет параболический цилиндр |
|||
с образующими, параллельными оси Oz. Направляющей цилиндрической поверхности является парабола x2 = 4y, z = 0 . □
Поверхности (2), (3), (4) схематически изображены на рисунках 1, 2, 3.
Рис. 1 |
Рис. 2 |
153
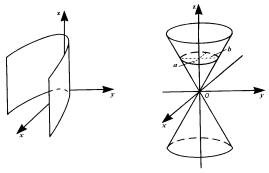
Рис. 3 |
Рис. 4 |
30. Конические поверхности. Конической называется поверх-
ность, описываемая прямой (образующей), движущейся вдоль некото- рой линии (направляющей) и проходящей через некоторую точку (вершину). Уравнение конуса второго порядка с вершиной в начале координат, осью которого служит ось Oz, записывается в виде
|
x2 |
+ |
y2 |
− |
z2 |
= 0 . |
|
|
|
|
|
|
|
(5) |
|||||
|
a2 |
b2 |
c2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Геометрически коническую поверхность можно изобразить, как |
|||||||||||||||||||
показано на рис. 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, уравнения |
|
x2 |
|
− |
y2 |
+ |
z2 |
= 0 , |
− |
x2 |
+ |
y2 |
+ |
z2 |
= 0 |
||||
|
a2 |
b2 |
c2 |
a2 |
b2 |
c2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох.
Пример 4. По какой линии пересекается конус x2 + y2 − 2z2 = 0
с плоскостью y = 2 ? |
|
|
|
|
|
Решение. |
Исключив |
из системы уравнений у, получим |
|||
x2 + 4 − 2z2 = 0 |
или |
z2 |
− |
x2 |
=1 . Значит, искомой линией пересечения |
2 |
|
||||
|
|
4 |
|
||
будет гипербола, лежащая в плоскости y = 2 ; ее действительная ось
параллельна оси Oz, а мнимая – оси Ох. □
Пример 5. Составить уравнение конической поверхности, вершиной которой служит точка М(1;1;1), а направляющей – эллипс
(x −1)2 |
(y −1)2 |
|
|||
|
|
+ |
|
|
=1, z = 3 . |
25 |
|
|
9 |
||
|
|
|
|
||
|
Решение. Составим уравнение образующей АМ, где |
||||
A(x0; y0; z0 ) |
– точка, лежащая на эллипсе. Это уравнение имеет вид |
||||
|
154 |
|
|
|
|
|
x −1 |
= |
|
y −1 |
|
= |
z −1 |
. |
Так |
как точка |
А лежит на |
эллипсе, |
то ее |
||||||||||||||||||||||||||||||||
|
|
|
y |
|
−1 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x −1 |
|
|
|
z |
0 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
координаты |
|
|
|
|
|
удовлетворяют |
|
|
|
|
|
|
|
уравнению |
эллипса, |
т.е. |
|||||||||||||||||||||||||||||
|
(x −1)2 |
|
(y |
|
−1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
|
|
+ |
|
|
|
0 |
|
|
|
|
|
|
=1, |
z0 = 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
25 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Исключив x0 , y0 , z0 из системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
x −1 |
|
|
|
z −1 |
|
|
y −1 |
|
|
z −1 |
|
|
|
(x −1)2 |
(y |
0 |
−1)2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
, |
|
|
|
|
= |
|
|
|
, |
|
|
0 |
|
+ |
|
|
|
|
|
=1, z0 = 3, |
|
||||||||
|
|
|
x0 −1 |
|
z0 −1 |
y0 |
−1 |
z0 −1 |
|
|
|
|
|
|
|
|
9 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
получим уравнение искомого конуса |
|
(x −1)2 |
+ |
(y −1)2 |
− |
(z −1)2 |
= 0 . □ |
||||||||||||||||||||||||||||||||||||||
|
|
25 |
|
|
|
|
9 |
|
9 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
40. Пары плоскостей. Пара пересекающихся плоскостей задается |
|||||||||||||||||||||||||||||||||||||||||||
уравнением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
− |
|
y2 |
|
|
= 0 , |
|
|
|
|
|
|
|
|
|
|
(6) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пара параллельных плоскостей задается уравнением |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
=1, |
|
|
|
|
|
|
|
|
|
|
|
(7) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а пара совпадающих плоскостей – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
(8) |
||||||||
|
|
Пример 6. Какую поверхность определяет в пространстве урав- |
|||||||||||||||||||||||||||||||||||||||||||
нение z2 = xz ? |
|
|
|
|
|
|
|
|
|
|
z2 = xz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Решение. |
Уравнение |
|
может быть представлено в виде |
||||||||||||||||||||||||||||||||||||||||
|
z(z − x) = 0 |
|
|
и распадается на два уравнения z = 0, z = x , т.е. оно опреде- |
|||||||||||||||||||||||||||||||||||||||||
ляет две пересекающиеся плоскости – плоскость Оху и биссектральную плоскость z = x , проходящую через ось Оу. □
§ 17. Эллипсоид
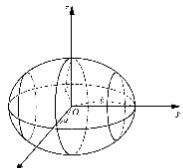
Эллипсоидом (рис. 1) называется п о в е р х н о с т ь , о п р е д е л я е м а я в декартовой системе координат Oxyz
к а н о н и ч е с к и м у р а в н е н и е м
x2 |
+ |
y2 |
+ |
z2 |
=1, |
(1) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
где величины а, b, c называют полуосями эллипсоида.
155

И з уравнения (1) вытекает, что координатные плоскости являются плоскостями симметрии эллипсои-
д а , а начало координат – |
центром симметрии . |
||||
Точки пересечения осей координат с эллипсоидом |
|||||
называют вершинами эллипсоида. |
плоскостью z = h, |
|
h |
|
< c , |
Рассмотрим сечение эллипсоида |
|
|
|||
|
|
||||
параллельной плоскости Оху. Тогда линия, которая получается в сечении, определяется системой уравнений:
|
|
|
|
|
x2 |
+ |
|
y2 |
=1− |
h2 |
, z = h . |
|
(2) |
|
|
|
|
|
|
a2 |
|
b2 |
c2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
Обозначим |
k2 =1− |
h2 |
|
и |
|
перепишем |
(2) |
в виде |
|||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
||
x2 |
+ |
y2 |
=1, z = h . |
|
|
|
|
|
|
|
|
|
||
(ak)2 |
(bk)2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Таким образом, |
сечение |
эллипсоида |
(1) |
плоскостью |
|||||||||
z = h, где h < c , представляет собой эллипс с полуосями ak и bk. Если
h = ±c , то этот эллипс стягивается в точку – вершину эллипсоида
(0;0;+с) или (0;0;−c) .
Аналогичная картина получается при рассмотрении сечений эллипсоида плоскостями, параллельными координатным плоскостям Oxz и Oyz. Заметим только, что плоскость Oхz пересекает эллипсоид по эллипсу, который определяется системой
|
x2 |
+ |
z2 |
=1, |
|
y = 0 , |
|
||||||
|
a2 |
c2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
плоскость Oyz – по эллипсу, определяемому уравнениями |
|
||||||||||||
|
y2 |
|
+ |
z2 |
|
=1, |
|
x = 0 . |
|
||||
|
b2 |
|
c2 |
|
|
a = b , из (1) |
|||||||
|
|
|
|
|
|
|
|
|
|||||
Если две полуоси эллипсоида равны, например |
|||||||||||||
получаем уравнение |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
+ |
y2 |
+ |
z2 |
=1. |
(3) |
|||||
|
|
a2 |
a2 |
c2 |
|||||||||
|
|
|
|
|
|
|
|||||||
Если пересечь эллипсоид (3) |
плоскостью z = h , |
то получим |
|||||||||||
окружность |
|
|
|
|
|
|
|
|
|
|
|
||
x2 + y2 = (1− h2 )a2 , z = h c2
156

с центром на оси Oz. Поэтому такой эллипсо- ид можно получить вращением расположен-
ного в плоскости Oхz эллипса x2 + z2 =1 во- a2 c2
круг оси Oz. Эллипсоид (3) называют эллипсои-
д о м |
в р а щ е н и я . |
Отметим также, что в случае a = b = c эл- |
|
л и п с о и д я в л я е т с я с ф е р о й .
§18. Гиперболоиды
10. Однополостный гиперболоид. Однопо-
Рис. 1 лостным гиперболоидом называется поверхность, которая в декартовой системе координат Oxyz определяется канониче-
ским уравнением
x2 |
+ |
y2 |
- |
z2 |
=1. |
(1) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
Установим форму поверхности (1). Для этого рассмотрим сечения ее координатными плоскостями Oxz и Oyz. Получаем соответственно системы уравнений:
ì x2 |
- |
z2 |
=1, |
|
ï |
|
|
||
|
c2 |
|||
ía2 |
|
|
||
ï |
|
|
|
|
îy = 0, |
|
|||
ì y2 |
- |
z2 |
=1, |
|
|
ï |
|
|
(2) |
||
|
c2 |
||||
íb2 |
|
|
|||
ï |
|
|
|
|
|
îx = 0. |
|
|
|
||
Из (2) следует, что в сечениях будут гиперболы соответственно в п л о с к о с т я х O x z и O y z .
Рассмотрим теперь сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Оху. В сечениях полу- ч и м л и н и и , о п р е д е л я е м ы е с и с т е м о й у р а в н е н и й
Введя величины a1 = a 1+ h2
c2
тему (3) в виде
ì x2 |
+ |
y2 |
=1+ |
h2 |
, |
|
|
ï |
|
|
|
(3) |
|||
|
b2 |
c2 |
|||||
ía2 |
|
|
|
||||
ï |
|
|
|
|
|
|
|
îz = h. |
|
|
|
|
|
||
и b1 = b 1+ h2 , перепишем сис- c2
157

ì x2 |
+ |
y2 |
=1, |
|
|
ï |
|
|
( 3′ ) |
||
|
b 2 |
||||
ía 2 |
|
|
|||
ï |
1 |
|
1 |
|
|
îz = h. |
|
|
|
||
Из ( 3′ ) заключаем, что плоскость z = h пересекает гиперболоид по эллипсу с полуосями а1 и b1.
Рассмотренные сечения показывают, что однополостный гипер- болоид изображается в виде бесконечной трубки, бесконечно расши- ряющейся в обе стороны по мере удаления от плоскости Оху (рис. 1).
Величины a, b, c называются полуосями однополостного гипер- болоида.
20. Двуполостный гиперболоид. Двуполостным гиперболоидом
называют поверхность, определяемую в декартовой системе координат Oxyz каноническим уравнением
x2 |
+ |
y2 |
- |
z2 |
= -1. |
(4) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
Для установления формы поверхности (4) рассмотрим сечения этой поверхности координатными плоскостями Oxz и Oyz. Получим
соответственно системы уравнений
ì x2 |
- |
z2 |
= -1, |
ì y2 |
- |
z2 |
= -1, |
||
ï |
|
|
ï |
|
|
||||
|
c2 |
|
c2 |
||||||
ía2 |
|
|
и íb2 |
|
|
||||
ï |
|
|
|
|
ï |
|
|
|
|
îy = 0 |
|
|
îx = 0, |
|
|
||||
из которых вытекает, что сечения представляются гиперболами. Изучим теперь сечения гиперболоида (1) плоскостями z = h . В сечениях
получаем линии
ì x2 ïía22 ïîz =
+ y2 =1,
b22
h,
ì x2 |
+ |
y2 |
= |
h2 |
-1, |
|
ï |
|
|
|
|||
|
b2 |
c2 |
||||
ía2 |
|
|
|
|||
ï |
|
|
|
|
|
|
îz = h |
|
|
|
|
||
|
|
|
|
|
|
(5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
где a |
2 |
= a |
h2 |
-1 и b = b |
|
h2 |
-1 . |
|||||
|
|
|
|
|
|
|||||||
|
|
c2 |
2 |
|
c2 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
При |
|
h |
|
> c (c > 0) |
плоскость |
||||||
|
|
|
||||||||||
или
z = h
пересекает гиперболоид по эллипсу с полу- осями а2 и b2, причем при увеличении h величины а2 и b2 также увеличиваются.
Если |
|
h = ±c , то из |
системы (5) получаем только две точки: |
||
(0;0;+с) и |
(0;0;−c) , и поэтому плоскости z = ±h касаются данной по- |
||||
верхности. |
|
h |
|
< c система |
|
При |
|
|
(5) определяет мнимый эллипс, т.е. плос- |
||
|
|
||||
кость z = h не пересекается с гиперболоидом (4).
Рассмотренные сечения позволяют изобразить двуполостный гиперболоид в виде поверхности, состоящей из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши (рис. 2).
Величины a, b, c называют полуосями двуполостного гиперболоида. Если полуоси a и b гиперболоида (однополостного или двуполост- ного) равны, то он называется гиперболоидом вращения и получается
вращением вокруг оси |
Oz гиперболы |
x2 |
− |
z2 |
|
=1, y = 0 в случае одно- |
|||||
a2 |
c2 |
||||||||||
|
|
|
|
|
|
|
|||||
полостного гиперболоида и гиперболы |
|
x2 |
− |
|
z2 |
= −1, y = 0 в случае |
|||||
|
a2 |
|
c2 |
||||||||
|
|
|
|
|
|
|
|
||||
двуполостного гиперболоида.
§ 19. Параболоиды
Эллиптическим параболоидом (рис. 1) называется поверхность,
определяемая в декартовой системе координат Oxyz каноническим
уравнением
z = |
x2 |
+ |
|
y2 |
. |
(1) |
|
a2 |
|
b2 |
|||||
|
|
|
|
|
|
||
Гиперболическим параболоидом (рис. 2) называется поверхность, |
|||||||
определяемая каноническим уравнением |
|
|
|||||
z = |
|
x2 |
− |
|
y2 |
. |
(2) |
|
a2 |
|
b2 |
||||
|
|
|
|
|
|
||
159
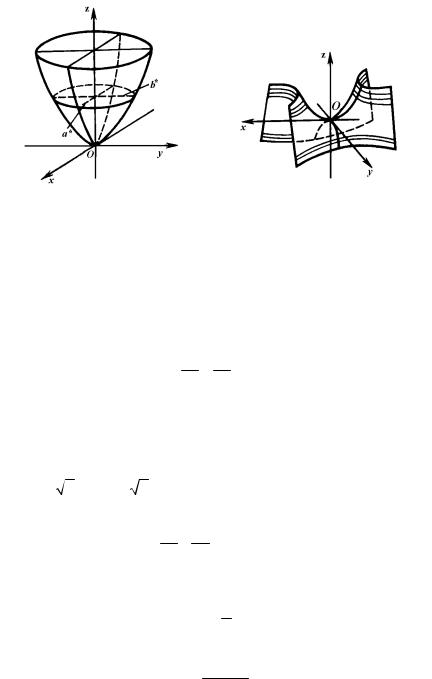
Рис. 1. |
Рис. 2. |
Из уравнений (1) и (2) вытекает, что плоскости Oxz и Oyz являются плоскостями симметрии параболоидов.
Ось Oz называется осью параболоида, а точка ее пересечения с поверхностью параболоида – вершиной.
Оба параболоида плоскостями, параллельными координатным плоскостям Oxz и Oyz, пересекаются по параболам. Например, плос- кость x = h пересекает эллиптический параболоид по параболе
z − h2 = y2 , x = h . a2 b2
Из уравнения (1) заключаем, что плоскость z = h (h > 0) , парал- лельная плоскости Oxу, пересекает эллиптический параболоид по эллипсу
x2 |
+ |
y2 |
=1, z = h , |
|
(a*)2 |
(b*)2 |
|||
|
|
где a* = a
 h и b* = b
h и b* = b
 h . Из уравнения (2) получаем, что плоскость z = h (h ¹ 0) пересекает гиперболический параболоид по гиперболе
h . Из уравнения (2) получаем, что плоскость z = h (h ¹ 0) пересекает гиперболический параболоид по гиперболе
x2 − y2 = h, z = h . a2 b2
Плоскость Оху пересекает гиперболический параболоид по двум пересекающимся прямым
x = ± ba y, z = 0 .
При a = b эллиптический параболоид, заданный уравнением
z = x2 + y2 , a2
160

называется параболоидом вращения. Он получается при вращении
параболы z = x2 , y = 0 вокруг оси Oz. a2
Задания для самостоятельной работы
1. Найти множество точек, координаты x, y которых удовлетворяют уравнению x + y =1 .
2. Установить, какое множество точек задает неравенство x2 + y2 £ 4x + 4y .
3.На плоскости даны точки А и В. Найти множество точек плоскости, удаленных от А вдвое дальше, чем от В.
ìïx2 + y2 =1, 4. Установить, при каких значениях параметра а система í
ïîx + y = a
не имеет решений, имеет единственное решение, имеет бесчислен- ное множество решений.
5.Составить уравнение прямой, отсекающей на оси Oy отрезок b = 4
иобразующей с осью Ox угол α = π4 .
6.Построить прямую, заданную уравнением y = 0,75x + 2.
7.Составить уравнение прямой, проходящей через точку М (2; 1) и
образующей с осью Ox угол α = π6 .
8.Составить уравнение прямой, проходящей через точки M1(3;1) и
M2 (5; 4) .
9.Дано общее уравнение прямой 12x − 5y − 65 = 0 . Написать уравнение этой прямой с угловым коэффициентом.
10.Прямая задана уравнением 3x − 5y +15 = 0 . Составить для этой прямой уравнение «в отрезках» и построить прямую.
11.Установить, какую линию описывает середина отрезка между двумя пешеходами, идущими по двум взаимно перпендикулярным дорогам с одинаковой скоростью (рассмотреть все возможные случаи).
161
12.Прямые заданы уравнениями y = x − 0,5 и y = 2x +1. Найти угол между этими прямыми.
13.Показать, что прямые 3x − 5y + 7 = 0 и 10x + 6y − 5 = 0 перпенди- кулярны.
14.Показать, что прямые x + y −1 = 0 и 2x + 2y − 3 = 0 параллельны.
15. Прямая L задана уравнением x − 5y +11 = 0 и дана
точка М (5; 2). Найти расстояние d от точки М до прямой L.
16.Найти уравнение прямой, проходящей через точку пересечения прямых 2x − 3y −1 = 0 и 3x − y − 2 = 0 и перпендикулярной прямой y = x +1.
17.Составить уравнение плоскости, проходящей через
линию пересечения плоскостей x + y + 5z −1 = 0, 2x + 3y − z + 2 = 0 и через точку М(3; 2;1).
18.Составить уравнение плоскости, проходящей через точку М(2; 3; 4) и перпендикулярной к оси Ox.
19.Записать уравнение плоскости, проходящей через
|
ось Oy и точку М(1; 2; 3). |
|
|
20. Найти |
расстояние |
между |
плоскостями |
x − 3y + 6z −12 = 0 и 2x − 6y +12z + 36 = 0 .
21. Найти угол между двумя плоскостями:
а) 4x − 5y + 3z −1 = 0, x − 4y − z + 9 = 0;
б) x − 3y + z + 5 = 0, 5x − 3y + z −1 = 0 .
22.Найти угол между плоскостями, проходящими через точку М(1; 3; 4), одна из которых содержит ось Oy , другая – ось Oz .
23. Две грани куба |
лежат соответственно на плоскостях |
3x − 2y + 6z − 7 = 0, |
3x − 2y + 6z − 35 = 0 . Вычислить объем |
этого куба. |
|
24. Написать канонические уравнения следующих пря-
|
|
|
мых: |
|
|
а) |
ì3x - 2y + z - 4 = 0, |
б) |
ìx + 2y + z - 4 = 0, |
||
í |
= 0; |
í |
= 0. |
||
|
î5x + 2y - 3z - 4 |
|
î2x - y + 2z - 3 |
||
162
