Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

6.54 Mб

Скачать

☆

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 4222 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Краткий курс школьной математики	211

3.(ax2 + bx + c)′ = 2ax + b , где a, b, c R, a ≠ 0 .

4.(xn )′ = nxn −1 , где n N .

Верна и формула (xr )′ = rxr −1 , где r R .

(4)Таблица производных.

1.(c)′ = 0 , где c = const ;

2.(xn )′ = nxn −1 , где n R ;

		1
3. (	x )′ =
				, т.к.
				, т.к.
	2		x

		1	′	1	, т.к. (x
4.			= −
				2
	x			x

′

−

x 2

;

−1 )′ = − x−2 = −

;

5.(sin x)′ = cos x ;

6.(cos x)′ = − sin x ;

(tg x)′ =

;

cos2

(ctg x)′ = −

;

sin 2 x

(a x )′ = a x ln a - производная показательной функции, где ln a - на-

туральный логарифм основания a > 0, a ≠ 1 - см. темы XXI – XXII.

10. (ex )′ = e x -

производная показательной

функции

с основанием

e ≈ 2, 72 .

11. (loga x)′ =

- производная логарифмической

функции,

где

x ln a

loga x - логарифм по основанию и числа

x , где a > 0, a ≠ 1 -

см.

Темы XXI – XXII.

212	В.А.Битнер

12. (ln x)′ = 1 - производная натурального логарифма. x

13. (arcsin x)′ =

;

1 − x

14. (arccos x)′ = −

;

1 − x

15. (arctg x)′

;

1 + x

16. (arcctg x)′ = −

1 + x

Решение упражнений.

Найти производные функций.

p 1

(x5 + 4x3 − 7 x2 + 6)′ = 5x4 +12x2 − 14x ;

p 2

′

−

′

−

x 2

+ x

7 = −

2 +

7 =

−

;

7 7 x5

x x

2 x x

p 3

′

1 + x2 − 2x

1 − x2

;

(1 + x2 )2

1 + x

p 4

p 5

′

2 −

4 x3

(7 − x2 )

(7 − x2 ) +

+ 4 x3

2 −

x + x 4

2 −

′

−

4 3

×(7 − x

)

= −

− x

)+ 2

−

(−2 x ) =

−

(7 − x2 ) − 2x

−

+ 4 x3

f ( x) = x − 4

Дано:

x , найти f ′ (4) ; f ′ (0, 01) ; f ′ (2 − x) .

Решение:

Краткий курс школьной математики	213

p10

p11

p12

f ′ ( x) = (x − 4							)′ = 1 −			2			; f ′ (4) = 1 −					2	=			1	;
					x					2								2				1


												x			4						2			;
																								;
f ′ (0, 01) = 1 −						2		= 1 − 20 = −19; f ′ (2 − x)													= 1 −			2


						0, 01																		2 − x
						0, 01																		2 − x
((2x − 7)14 )′ = 14 (2x − 7) (2x − 7)′ = 28 (2x − 7) ;
(3				)′ =				1						′	1	(9x2 −16)−			2	(9 x2 − 16)′ =
			2 − 16			(9x2		− 16)						=
		9x									3								3
		9x									3								3
															3
=			1			18x		=						6x			;


	3 3 (9 x2 − 16)
	3 3 (9 x2 − 16)								3 (9x2 − 16)2

(3 cos (2, 3x −10π ))′ = −3 sin (2, 3x −10π ) 2, 3 = −6, 9 sin (2, 3x − 10π ) ;

′

5 tg (2x + 3) + 2 tg

;

(2 x + 3)

cos2

(4 ctg (2t + 3))′ = −

;

sin 2

(2t + 3)

(arcsin x2 )′

2 x

;

1 − x

(arcctg2 (x3 − 2 x + 1))′ = 2 arcctg (x2 − 2 x + 1) (arcctg (x3 − 2 x + 1))′ ×

× (x3 − 2 x + 1)′ = 2 arcctg (x3 − 2 x + 1)	−1	(3x2 − 2) =
	1 + (x3 − 2 x + 1)2

2 (3x2 −1)arcctg (x3 − 2 x + 1)

= −

1 + (x3 − 2 x + 1)2

Упражнения для самостоятельного решения

Найти производные функций

214	В.А.Битнер

p10

p11

p12

p13

p14

p15

(7 x5 + 2

)′ ;

′

− 3x4

;

4x2

′

x −

;

1 + 2x ′

;

3 −

x3 + 2

′

;

4 + x + x

Дано: f ( x)

= x2 − 3x , найти f ′ (0) ; f ′ (−1) ; f ′ (2) ; f ′ ( x +1) ;

((3 + 5x)10 )′ ;

((5x − 2)13 − (3x + 7)20 )′ ;

(4x2 − 1)′ ;

(2 x2 − 30 cos (5x + 6))′ ;

(3 tg (2x +1))′ ;

(7 ctg (2 x − π ))′ ;

(arccos2 x)′ ;

(5 arctg (2x2 − 3x +1))′ ;

(sin3 x)′ .

Ответы:
p 1	35x4 +	1		;
	35x4 +			;
			x

Краткий курс школьной математики	215

p 2

−

− 12x3 ;

p 3

10x

x +

;

3x2 3 x2

p 4

;

p 5

(3 − 5x)2

+ 2 x

+12x

− 4 x − 2

;

(4 + x + x

2 )2

p10

p11

f ′ (0) = −3; f ′ (−1) = −5; f ′ (2) = 1; f ′ ( x +1) = 2x −1; 50 (3 + 5x)9 ;

65 (5x − 2)12 − 60 (3x + 7)19 ;

4x ;

4 x2 − 1

4x +150 sin (5x + 6) ;

cos2 (2x + 1) ;

p 12	−	14			;

		sin 2
				2 x
p 13	−	2	arccos			x	;


				2
		1 − x
p 14		5 (4x − 3)								;

	1 + (2x2 − 3x +1)2
p 15	3sin 2			x cos x =				3	sin 2 x sin x .

				2

(5)Уравнение касательной к кривой. Геометрический смысл производной.

Пусть имеем кривую y = f ( x) , AM - касательная к этой кривой в точ-

ке M ( x0 ; y0 ) - см. рис.1.

Тогда уравнение этой касательной имеет вид:

216	В.А.Битнер

рис. 1

y − y0 = f ′ ( x0 ) ( x − x0 ) ,	где
y = f ( x0 ) и M ( x0 ; y0 )	- точка каса-
ния.

Геометрический смысл производной: f ′ ( x0 ) = tg α , где α -

угол касательной к графику функции y = f ( x) в точке касания ( x0 ; y0 ) с положительным направлением оси

0x .

Найти тангенс угла наклона касательной к графику функции занной точке:

p 1

f ( x) = x2 , M (−3; 9) .

Решение:

f ′ ( x) = 2x; x0 = −3; tg α = f ′ (−3) = −6 .

p 2

Ответ: −6 .

f ( x) =

4x − x

; M

(0; 0)

; M

(2;1) ; M

(4; 0) .

′

f ′ ( x) = x

−

= 1 −

x; tg α1 = f ′ (0) = 1; tg α 2 = f ′ (2)

tg α3 = f ′ (4) = −1 , откуда α1 = 450 ,α 2 = 00 ,α3 = 1350 .

Ответ: 1; 0; −1 .

f в ука-

= 0;

Написать уравнение касательной к графику функции f в точке с указанной абсциссой:

p 3

y =

; x = −1.

Решение:

′

Имеем x0 = −1; y0

= −3; y ′ =

f ′ ( x) =

= −

;

−1

f ′ (−1) = −

= −3 ;

тогда уравнение касательной имеет вид:

(−1)2

Краткий курс школьной математики

217

y + 3 = −3 ( x + 1)

или y = −3x − 6 .

Ответ:

y = −3x − 6 .

p 4

y =

, x

= 4 .

Решение:

Имеем

= 4; y

= 2; f ′ ( x) = (

)′ =

;

f ′ (4) =

, тогда имеем уравнение касательной

y − 2 =

( x − 4)

или y =

x + 1. Ответ: y =

x + 1.

p 5

y = tg x; x =

Решение:

Имеем x

; y = tg

= 1; f ′ ( x) = (tg x)′ =

;

cos2

f ′

= 2 , тогда уравнение касательной имеет вид

cos

2 π

y − 1 = 2 x −

или y = 2x +1 +

Ответ: y = 2x +1 + π . 2

Упражнения для самостоятельного решения.

Найти тангенс угла наклона касательной к графику функции f в указанной точке:

p 1	f ( x) = −	2	; M (1; −2) ;

		x
p 2	f ( x) = x3 ; M (−2; −8) ;

Написать уравнение касательной к графику функции f в точке с указанной абсциссой:

p 3 y = x3 , x = 2 ;

218

В.А.Битнер

p 4

y = 2 sin 2x, x =

;

p 5

В какой точке графика функции y =

x касательная наклонена

к оси абсцисс под углом в 450 ?

Ответы:

p 1

p 2

p 3 y = 12x − 16

p 4

p 5

y = 2x + 3 −

;

4 2

(6) Применение производной в физике.

Пусть точка движения по прямой и в момент времени t находится в точке с координатой x (t ) . Тогда V (t ) = x′ (t ) - скорость точки в любой

момент времени t .
Если точка движется по закону	x (t ) = pt	2 + qt + r p ≠ 0 ,	(1)
		1
то V (t ) = x′ (t ) = 2 p + q ,			(2)
a (t ) = V ′ (t ) = 2 p -			(3)

скорость изменения скорости в движении, заданном формулой (1) – это ускорение точки в момент времени t . В этом случае a = co nst .

e p > 0 , то движение равноускоренное, e p < 0 - то равнозамедленное.

Верно и обратное утверждение. Из (3) получаем p = a , при t = 0 2

x0 = x (0) = r , V0 = V (0) = q . Поэтому формулу (1) можно переписать в

виде x (t ) =	at 2	+ V t + x ,		(4)

2		0	0

где V0 - начальная скорость,				x0 - начальная координата, a - ускорение.
Формула (4) – это закон равнопеременного движения.
p 1 Тело движется по закону x (t ) = 2t 3 + t −1 (см).
Найти ускорение a				в момент времени t . В какой момент

Краткий курс школьной математики

219

см

времени a = 1

, a =

сек2

Решение:

Имеем a (t ) = x′′ (t ) = (6t 2 +1)

′ = 12t

см

e a = 1, то

сек2

12t = 1, t =

сек

e a = 2 , то 12t = 2, t =

(сек)

Ответ: 12t

см

;

сек;

сек.

сек2

p 2 Тело движется по окружности по закону

ϕ (t ) = 3t 2 − 4t + 2 ( рад.)

Найти угловую скорость ω (t ) ,ω (4) .

Решение: ω (t ) = ϕ ′ (t )

= 6t − 4

рад

, ω

(4) = 24 − 4 = 20

рад

сек

Самостоятельно.

p 3

Тело массой

2 кг.

движется

прямолинейно по закону

x (t ) = t 2 + t + 1(см) , время t

измеряется в сек .

Найти: 1) действующую силу F ; 2)

кинетическую энер-

гию E тела через 2 сек. после начала движения.

p 4

Точка движется прямолинейно по закону x (t ) = t . Пока-

жите, что ее ускорение пропорционально кубу скорости.

Ответы:

p 3

1)0, 04H ; 2)25дж ;

p 4

Показать, что a (t ) V

3 (t ) .

(7)Применение производной при исследовании функций.

1. Достаточное условие возрастания (убывания) функций.

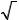
220								В.А.Битнер


t 1	1)	e для функции			f	на промежутке I		выполняется усло-
		вие	f ′ > 0	в каждой точке из I , то			f	возрастает на I .
	2)	e для функции			f	на промежутке I		выполняется усло-
		вие	f ′ < 0	в каждой точке из I , то			f	убывает на I .

2. Экстремумы функции.

oТочки, в которых производная равна 0 или не существует, называются критическими.

Необходимое условие существования экстремума.

t 2	e точка x0	является точкой экстремума для функции f ( x)
Ферма	и в этой точке существует производная, то она равна 0 , то
	есть f ′ ( x0 )	= 0 .

Так как теорема Ферма – лишь необходимое условие существования

экстремума, то из того, что		f ′ ( x0 ) = 0 не обязательно следует, что в
этой точке функция имеет экстремум.
Первое достаточное условие существования экстремума.
t 3	e функция f непрерывна в точке x0 и		f ′ ( x) > 0 на (a; x0 ) ,

	и f ′ ( x) < 0 на ( x0 ; b)	, то x0 - точка максимума функции f
	на (a; b) .

Короче говоря, e при переходе через точку x0			производная меняет
знак с плюса на минус, то x0		- точка максимума.
t 4	e функция f непрерывна в точке x0 и		f ′ ( x) < 0 на (a; x0 ) ,

	и f ′ ( x) > 0 на ( x0 ; b)	, то x0 - точка минимума функции f
	на (a; b) .

Короче говоря, e при переходе через точку x0			производная меняет
знак с минуса на плюс, то x0		- точка минимума.

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 4222 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.07.2019400.64 Кб4bestref-201996.rtf
#
12.03.20152.74 Mб10BhagavatGita_kak_ona_est.pdf
#
16.04.201995.65 Кб3Bilety_dlq_ekzamena_po_kursu_Socialogiq_i_psiho....docx
#
25.09.2019173.57 Кб3Bilety_IGA_po_190604TA4.doc
#
19.09.2019507.9 Кб7Biologia.doc
#
12.03.20156.54 Mб83Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki.pdf
#
08.09.2019652.29 Кб4biznes_plan_po_Petrulevich.doc
#
22.03.201663.12 Кб4breaking.pdf
#
12.03.2015931.33 Кб9Broshyura (1).doc
#
12.03.2015826.37 Кб7Broshyura.doc
#
23.11.2019823.3 Кб1Broshyura.doc