Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki
.pdf
222 |
В.А.Битнер |
|
|
3.Исследование функции с помощью производной
( Схема исследования функции – см. тему XI – (8) )
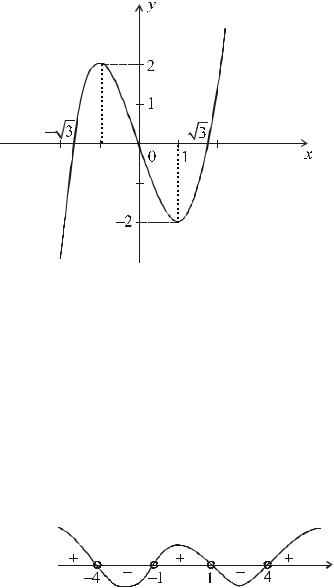
Исследовать функции и построить их графики. p 1 y = x3 − 3x .
1) D ( y ) = R ;
2) f (− x) = (− x)3 − 3(− x) = − x3 + 3x = − (x3 − 3x) = − f ( x) , сле-
довательно,функция нечетная и график ее симметричен началу координат;
3)при x = 0 y = 0 , то есть (0; 0) - точка пересечения графи-
ка с 0 y ;
|
y = 0 x3 − 3x = 0, x ( x2 − 3) = 0, x = 0, x |
|
|
|
|
|
||||||||
4) |
|
= ± |
3 , то |
есть |
||||||||||
|
1 |
2,3 |
|
|
|
|
||||||||
|
(0; 0) ; (− |
|
|
|
|
|
|
|
||||||
|
3; 0); ( 3; 0) - точки пересечения графика с 0x ; |
|||||||||||||
5) |
y > 0 x3 − 3x > 0 x (x + |
|
) (x + |
|
) |
> 0 |
|
то |
есть |
|||||
3 |
3 |
|
||||||||||||
|
|
|
y > 0, e x (− |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3; 0) ( 3; +∞) и y < 0, e x (−∞; − 3 ) (0; 3 ); |
||||||||||||||||||||||
6) |
|
y ′ = 3x |
2 − 3, y ′ = 0 3x |
2 − 3 = 0, x |
= ±1 |
- |
критические |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
( |
) |
|
−1 |
|
( |
|
) |
|
1 |
( |
1; |
+∞ |
) |
y |
max |
= |
y ( |
) |
|
|
|||
|
|
|
−∞; −1 |
|
|
|
|
|
−1;1 |
|
|
|
|
|
|
−1 = 2 |
|||||||||
y ′ |
|
+ |
|
0 |
|
|
− |
|
|
|
0 |
+ |
|
|
ymin |
= y (1) = −2 |
|||||||||
y |
|
|
|
2 |
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
Краткий курс школьной математики |
223 |
|
|
7)E ( y) = R ;
8)График – см. рис. 3.
|
рис. 3 |
|
|
|
p 2 y = x4 − 5x2 + 4 . |
|
|
|
|
1) |
D ( y ) = R ; |
|
|
|
2) |
f (− x) = (− x)4 − 5 (− x)2 + 4 = x4 − 5x |
2 + 4 = f ( x) |
- четная, |
|
|
график симметричен 0 y ; |
|
|
|
3) |
(0, 4) - точка пересечения графика с 0 y ; |
|
||
4) |
y = 0 x4 − 5x + 4 = 0, (x2 ) = 1, ( x2 ) |
|
= 4, x = ±1; x = ±2 , |
|
|
1 |
2 |
1,2 |
3,4 |
|
то есть (−2; 0) ; (−1; 0) ; (1; 0) ; (2; 0) |
- точки пересечения с |
||
|
0x . |
|
|
|
5) |
y > 0 x4 − 5x2 + 4 > 0 ( x +1) ( x − 1) ( x + 4) ( x − 4) > 0 |
|||
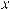то есть
y> 0, e x (−∞; −4) (−1; 4) (4; +∞) ;
y< 0, e x (−4; −1) (1; 4) ;
226 В.А.Битнер
2. y ′ = 0 4x ( x |
2 −1) = 0 x |
= 0, x = ±1 - критические |
|
1 |
2,3 |
точки.
3.f (−3) = 81 −18 + 5 = 68; f (−1) = 1 − 2 + 5 = 4; f (0) = 5; f (1) = ;
=f (−1) = 4; f (3) = f (−3) = 68
4.Получили " 4 " - наименьшее значение, "68" - наибольшее значение функции на [ −3; 3] .
Пишут:
min f ( x) = f (−1) = f (1) = 4, max f ( x) = f (−3) = f (3) = 68 . |
|
[−3;3] |
[−3;3] |
Ответ: 4; 68 .
(9)Задачи на наименьшее и наибольшее значения.
Алгоритм решения таких задач.
1.Из числа переменных величин в данной задаче выбираем аргумент и находим область его изменения.
2.Выражаем через аргумент функцию, наибольшее или наименьшее значение которой надо найти.
3.Находим значение аргумента, при котором функция принимает наименьшее или наибольшее значение и определяем соответствующее значение функции.
Решение задач. |
|
|
|
|
|
|
|
Задача 1. |
Вписать в круг радиуса R прямоугольник наибольшей пло- |
||||||
|
щади. |
|
|
|
|
|
|
|
Решение: |
|
|
|
|
||
|
1. |
n |
x |
- длина одной из сторон |
|||
|
прямоугольника, |
где |
0 ≤ x ≤ 2R , |
тогда |
|||
|
|
4R2 − x2 |
- длина другой стороны. |
|
|||
|
2. |
Площадь прямоугольника |
|
||||
|
S ( x) = x |
4R2 − x2 . |
|
|
|||
Краткий курс школьной математики |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
227 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. S ′ ( x) = (x |
|
|
)′ = |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4R2 − x2 |
4R2 − x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
−2 x |
|
|
4R |
2 − x2 − x2 |
4R2 − 2x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
+ x |
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 4R2 − x2 |
|
|
|
4R2 − x2 |
|
|
4R2 − x2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
S ′ ( x) = 0 при x = ±R 2 и S ′ ( x) не существует при x = ±2R . Это |
|||||||||||||||||||||||||||||||||
критические точки. |
Так как 0 ≤ x ≤ 2R , то надо сравнить значения |
||||||||||||||||||||||||||||||||
функции S ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
в точках x1 = 0, x2 |
= R 2, x3 = 2R и выбрать из этих |
|||||||||||||||||||||||||||||||
значений наибольшее. Имеем: |
S (0) = 0, S (R |
|
|
) = 2R |
2 , S (2R) = 0 . |
||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||
Отсюда max S ( x) = S (R |
|
) = 2R2 . Получили |
x = R |
|
|
|
- длина од- |
||||||||||||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||||||
|
|
[0;2 R] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
ной стороны, тогда |
|
4R2 − x2 = |
|
|
4R2 − 2R2 = R 2 |
- длина другой |
|||||||||||||||||||||||||||
стороны.
Ответ: среди прямоугольников, вписанных в круг радиуса R наи-
большую площадь имеет квадрат со стороной R
2 .
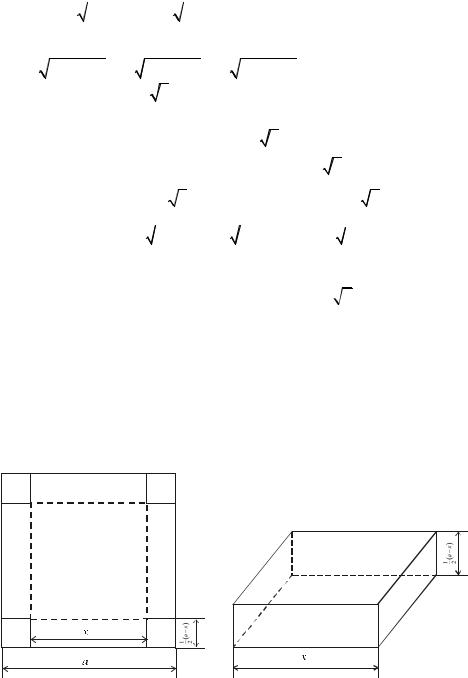
Задача 2. Из квадратного листа жести со стороной a надо изготовить открытую сверху коробку, вырезав по углам квадратики и загнув образовавшиеся кромки.
Какой должна быть сторона основания коробки, чтобы ее объем был наибольшим?
Решение:
228 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В.А.Битнер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1. |
Обозначим |
через x |
длину стороны основания коробки, где |
|||||||||||||||||||||||||||||||
|
0 < x < a . Тогда длины сторон вырезанных квадратиков равны |
|||||||||||||||||||||||||||||||||
|
|
1 |
(a − x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
Объем коробки V ( x) = |
1 |
x2 (a − x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x2 (a − x) ′ |
|
2 x |
(a − x) − x2 |
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||
3. V ′ ( x) = |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= ax − |
|
|
x2 , |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
V ′ ( x) = 0 ax − |
3 |
x2 |
= 0, x |
= 0, x |
= |
2 |
|
a - критические точки |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
функции. Будем искать наибольшее значение функции V ( x) на |
|||||||||||||||||||||||||||||||||
|
отрезке [0; a] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
V (0) = V (a ) = |
|
|
2 |
|
|
|
1 |
|
2 |
|
|
|
4 |
|
2 = |
2 |
a3 |
max V (x ) = |
|||||||||||||||
|
0,V |
|
a = |
|
a − |
|
|
|
|
|
|
|
|
a |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
3 |
|
|
|
9 |
|
|
27 |
|
[0;a] |
|||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
= V |
|
a = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: при длине основания коробки |
|
2 |
a |
ее объем будет наиболь- |
||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
шим. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 3. |
В арифметической прогрессии шестой член равен 3, раз- |
|||||||||||||||||||||||||||||||||
ность прогрессии d ≥ |
1 |
. При каком значении d |
произведение пер- |
|||||||
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
вого, четвертого и пятого членов будет наибольшим? |
||||||||||
Решение. |
|
|
|
|
|
|
|
|||
1. |
n первый член прогрессии a1 , |
тогда по формуле n − го члена |
||||||||
|
шестой |
|
член |
прогрессии равен a6 = a1 + 5d = 3 , откуда |
||||||
|
a1 = 3 − 5d , где |
|
|
|
|
|
||||
|
d ≥ |
1 |
, a = a + |
3d = 3 − 5d + 3d = |
3 − 2d , a = a − d = 3 − d . |
|||||
|
|
|||||||||
|
2 |
|
4 |
1 |
|
|
|
5 |
6 |
|
|
|
|
|
|
|
|
|
|
||
2. |
Обозначим произведение a1a4 a5 |
= P (d ) = (3 − 5d ) (3 − 2d ) (3 − d ) . |
||||||||
Краткий курс школьной математики |
229 |
|
|
3.P′ (d ) = ((3 − 5d )(3 − 2d )(3 − d ))′ = −5 (3 − 2d )(3 − d ) −
−2 (3 − 5d ) (3 − d ) − (3 − 5d ) (3 − 2d ) = −30d 2 +102d − 72, P′ (d ) = 0 −30d 2 + 102d − 72 = 0,10d 2 − 34d +12 =
= 0, 5d 2 −17d + 6 = 0 , |
D = 289 −120 = 169, d = |
17 − 13 |
= |
2 |
< |
1 |
- |
||
|
|
|
|||||||
|
|
1 |
10 |
5 |
2 |
|
|||
|
|
|
|
||||||
не удовлетворяет условию, d2 = 3, P′ (2) > 0, P ′ (4) < 0 . Так как |
|||||||||
при переходе через точку d = 3 производная P (d ) |
меняет знак |
||||||||
с плюса на минус, то из первого достаточного условия сущест- |
|||||||||
вования экстремума max P (d ) = P (3) . |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
;+∞ |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Ответ: при разности d = 3 .
|
Задача 4. Число 16 разбить на два положительных слагаемых так, |
|
чтобы сумма кубов этих слагаемых была наименьшей. |
|
Решение. |
1. |
n x - первое слагаемое, где 0 < x < 16 , тогда 16 − x - второе сла- |
|
гаемое. |
2. |
Обозначим сумму кубов этих слагаемых f ( x) = x3 + (16 − x)3 . |
3. |
f ′ ( x) = 3x2 − 3(16 − x)2 = 3(x2 − x2 + 32x − 256) = 96 ( x − 8) . |
f ′ ( x) = 0 x − 8 = 0, x = 8 - критическая точка.
+
4.f ′′ ( x) = 96 > 0 («вода наливается») и из второго достаточного
условия существования экстремума имеем max f ( x) = f (8) , тогда
(0;16)
второе слагаемое 16 − 8 = 8 .
Ответ: сумма кубов двух положительных слагаемых наименьшая, если каждое слагаемое равно восьми.
230 |
В.А.Битнер |
|
|
Упражнения для самостоятельного решения.
Задача 1. Как согнуть кусок проволоки данной длины l , чтобы площадь ограниченного ею прямоугольника была наибольшей.
Задача 2. Число 180 представить в виде суммы трех неотрицательных слагаемых так, чтобы два из них относились как 1 : 2 , а произведение трех слагаемых было наибольшим.
Задача 3. Требуется изготовить ящик с крышкой, объем которого был бы равен 72см3 , причем стороны основания относились бы как 1 : 2 . Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?
Задача 4. Какое положительное число, будучи сложенным с обратным числом, дает наименьшую сумму?
Задача 5. Покажите, что из всех равнобедренных треугольников, вписанных в данный круг, наибольшую площадь имеет равносторонний треугольник.
Задача 6. Из всех прямоугольников, вписанных в полукруг (одна сторона прямоугольника лежит на диаметре полукруга), найдите прямоугольник наибольшей площади.
Задача 7. Найдите наименьшее и наибольшее значения функции g ( x) = x3 − 3x2 + 3 на отрезке [1; 3] .
Задача 8. Найдите наименьшее и наибольшее значения функции f ( x) = x4 − 8x2 − 9 в промежутке [ −1;1] .
Ответы:
Задача 1. Прямоугольник должен быть квадратом .
Задача 2. e слагаемые равны 40, 60 и 80 , то их произведение наибольшее.