
Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki
.pdf


194 |
|
|
|
|
|
|
|
|
|
|
|
В.А.Битнер |
|
p13 |
|
5π |
+ π n | n Z |
|
|
|
|
|
|
|
|
|
|
± |
|
; |
|
|
|
|
|
|
|
|
|||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
p14 |
1; Указание: предварительно доказать, что |
|
|
|
|||||||||
|
|
|
|
arctg x + arcctg x = π ; |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
p15 |
1; |
|
|
|
|
p16 arctg 2 + π n; arctg |
1 + π n | n Z ; |
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
p17 |
|
|
1 |
|
|
p18 |
π |
|
|
|
|
|
|
-arctg |
+ π n | n Z ; |
|
n | n Z |
|
|
|
|||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
p19 |
π |
|
|
|
|
p20 |
|
−1) |
n |
1 |
|
|
|
|
n | n Z ; |
|
( |
|
arcsin |
+ π n | n Z . |
|
||||||
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
(21) |
Тригонометрические неравенства |
|
|
|
|||||||||
К простейшим тригонометрическим неравенствам относятся неравен- |
|||||||||||||
ства |
вида: |
T (kx + b ) > a, T (kx + b ) < a,T (kx + b ) ≥ a,T (kx + b ) ≤ a , |
где |
||||||||||
k , a, b R, k ≠ 0, T - знак любой из тригонометрических функций. В за- |
|||||||||||||
висимости от значения |
a и с учетом |
E (T ) эти уравнения могут не |
|||||||||||
иметь решений или иметь бесчисленное множество решений. Рассмот- |
|||||||||||||
рим решение тригонометрических неравенств на конкретных приме- |
|||||||||||||
рах. Решать их будем с помощью определений тригонометрических |
|||||||||||||
функций, единичной числовой окружности, осей |
|
y |
|
||||||||||
тангенсов и котангенсов – сначала графически, |
|
|
|
||||||||||
потом выписывать ответ. |
|
|
|
|
|
5π |
|
π |
|||||
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Решить неравенства. |
|
|
|
|
|
|
0 |
|
x |
||||
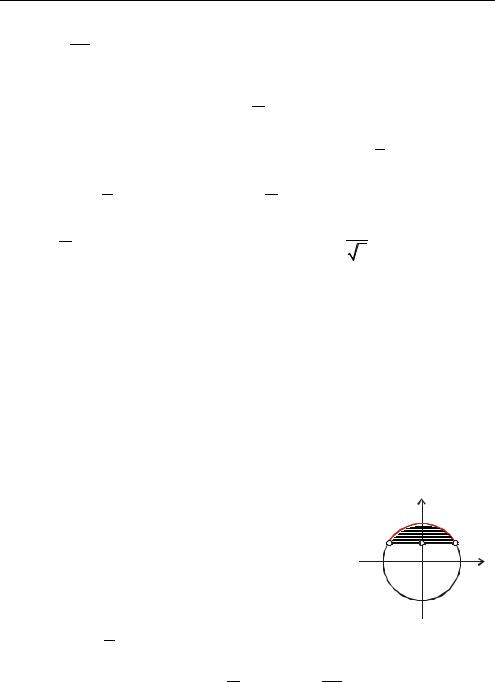
p11 |
sin x > 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
синус – это ордината π + 2π n < x < 5π + 2π n, n Z |
|
|
||||||||||
|
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
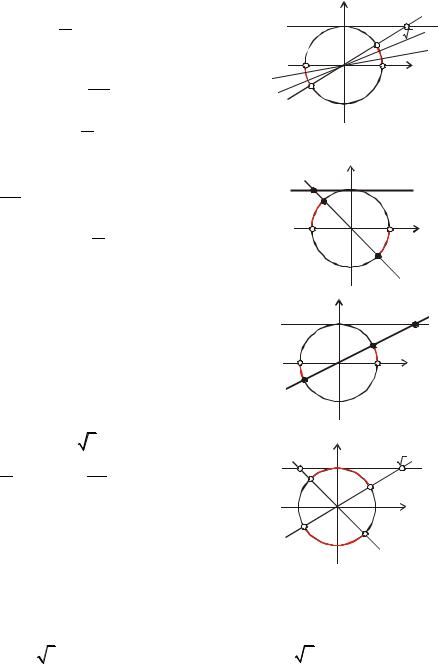
198 |
В.А.Битнер |
|
|
|
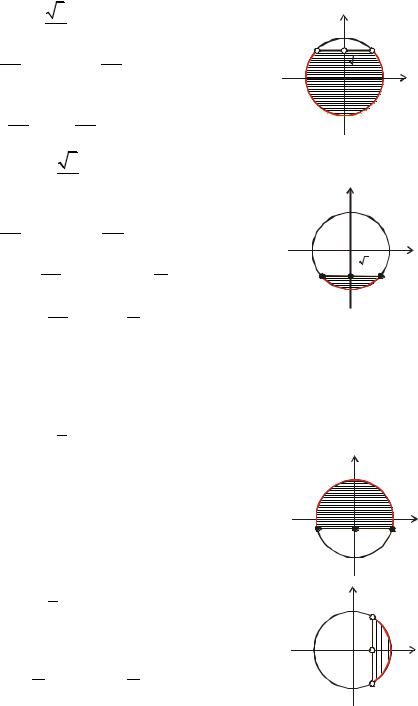
π n < x < π + π n, n Z или можно |
|
y |
|
|
|
||||
|
|
π |
|
|
3 |
|||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
записать ответ в виде |
π |
|
0 |
|
|||||
|
π + π n < x < 7π + π n, n Z , или |
|
0 |
|
|
x |
||||
|
7π |
|
|
|
|
|||||
|
|
|
|
|
6 |
6 |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
Ответ: |
π n; |
+ π n , n Z |
|
|
|
|
|
||
|
|
|
|
6 |
|
|
|
|
|
|
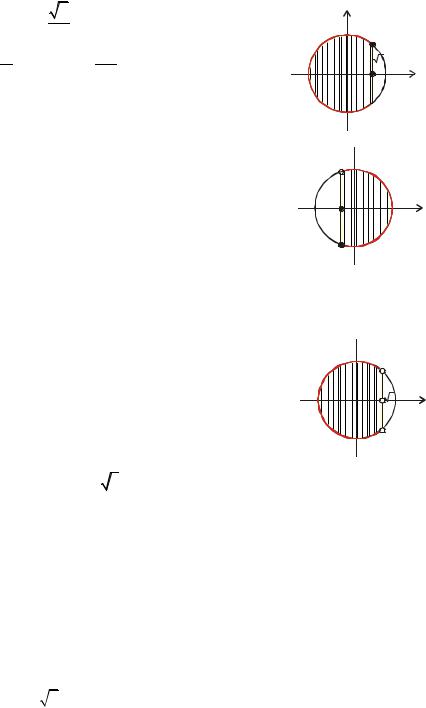
p20 |
ctg x ≤ −1 |
|
|
y |
|
|
|
|||
|
3π + π n ≤ x < π + π n, n Z |
|
|
|
|
|||||
|
−1 |
|
|
|
|
|||||
|
4 |
|
|
|
|
|
3π |
|
|
|
|
или в виде: − π + π n ≤ x < π n, n Z |
π |
4 |
|
0 |
|
||||
|
|
|
|
|||||||
|
|
0 |
|
|
x |
|||||
|
|
|
|
|
4 |
|
|
− |
π |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
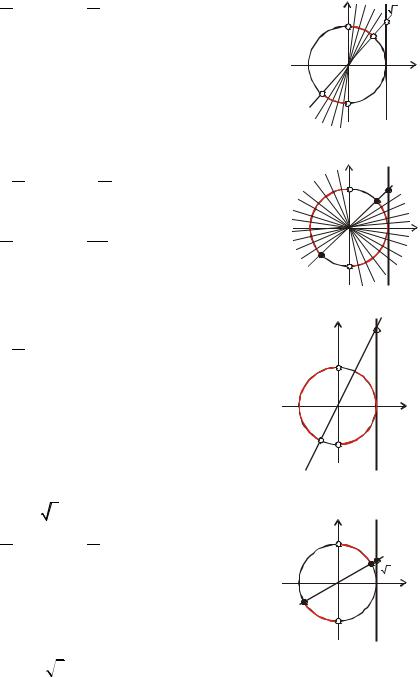
p |
ctg |
x |
≥ 2 |
|
|
|
y |
|
|
|
21 |
|
|
|
|
|
|
|
|
||
|
π n < x ≤ arcctg 2 + π n, n Z |
|
|
|
|
2 |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
arcctg 2 |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
x |
|
|
|
|
|
|
|
|
|
||
p22 |
−1 |
< ctg x < |
|
3 |
|
y |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
3π |
|
−1 |
3 |
|
+ π n < x |
< |
+ π n, n Z |
3π |
|
|||
|
6 |
4 |
|
|||||
|
|
|
|
|
4 |
π |
||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
0 |
x |
Упражнения для самостоятельного решения
p1 sin x > |
3 |
p2 |
cos x ≥ |
2 |
|
|
|
||||
2 |
2 |
||||
|
|
|


200 |
В.А.Битнер |
|
|
(22)Формулы аркфункций
С помощью основных тригонометрических тождеств, определений и свойств тригонометрических и обратных тригонометрических функций легко вывести формулы обратных тригонометрических функций.
1. Выразим тригонометрические функции через arcsin a .
1)sin (arcsin a ) = a ;
2)cos(arcsin a) = 1 − sin 2 (arcsin a) =  1 − a2 ;
1 − a2 ;
3) |
tg (arcsin a) = |
sin (arcsin a) |
= |
|
|
|
a |
|
|
|
; |
||
cos (arcsin a) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
1 − a |
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
1 − a |
2 |
|
|
|
||||
4) |
ctg (arcsin a) = |
|
|
= |
|
|
|
|
. |
||||
tg (arcsin a) |
|
|
|
a |
|||||||||
2. |
Выразим тригонометрические функции через arccos a . |
||||||||||||
1)cos (arccos a) = a ;
2)sin (arccos a) =  1 − a2 ;
1 − a2 ;
3) |
tg (arccos a) = |
|
1 − a2 |
|
; |
||||
|
|
|
|
||||||
|
|
a |
|
||||||
|
|
|
|
|
|
|
|
||
4) |
ctg (arccos a ) = |
|
a |
|
|
|
. |
||
|
|
|
|
||||||
|
|
|
|
|
|||||
1 − a |
2 |
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
Вывод этих формул аналогичен предыдущим. |
|||||||||
3. |
Выразим тригонометрические функции через arctg a . |
||||||||
1) tg (arctg a) = a ;
2) |
ctg (arctg a) = |
1 |
= |
1 |
; |
|
|
|
|
|
|
|
|
|
|
||
tg (arctg a) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||
|
cos (arctg a) = |
1 |
|
|
|
1 |
|
|
|
|
|
|
|||||
3) |
|
|
|
|
|
|
|
= |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 + tg2 (arctg a) |
1 + a2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
sin (arctg a ) = tg (arctg a) |
× cos (arctg a) = |
|
|
a |
|
|
. |
|||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||
|
1 + a |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Выразим тригонометрические функции через arcctg a .


 3 sin
3 sin 
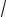 2 ;
2 ;
 3 −
3 − 
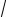 2 ;
2 ;
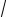 2; +∞
2; +∞ 7π 4
7π 4 y
y
 y
y
 3
3 arctg100
arctg100
 3
3