Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

e x и x - корни квадратного уравнения ax2 + bx + c = 0 , то выполняют-

ся соотношения

. Верна и обратная теорема.

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

6.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 428 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

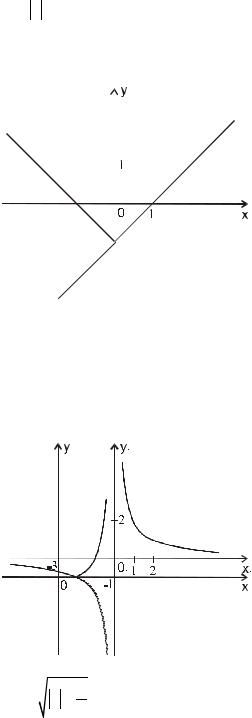
Краткий курс школьной математики	71

p 6

p 7

y = x −1 . При построении см. (4)-1.

1.Строим график функции y1 = x −1, x ≥ 0 .

2.Отобразим эту часть графика симметрично оси 0 y , получим искомый график.

y =

+ 1

x − 3

Вначале строим график функции y1 =

- см. (2) - p1

x − 3

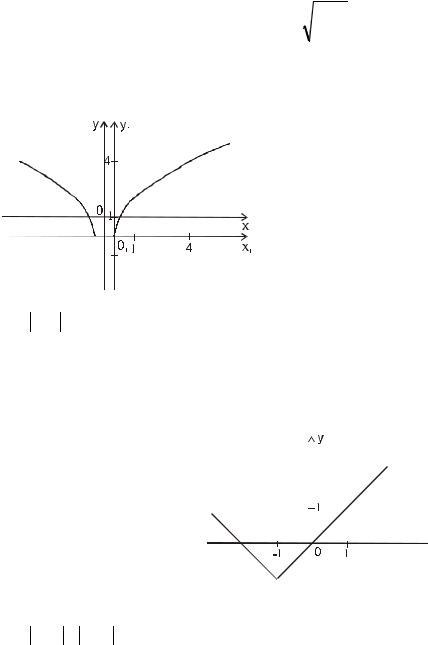
2.Часть графика, расположенную ниже оси 0x , отобразим симметрично оси 0x . Получим искомый график.

y = 2 x − 1 −1 . 2

72	В.А.Битнер

p 8

p 9

1. Вначале строим график функции y = 2 x −	1	−1 - см. (5) -

2

p1.

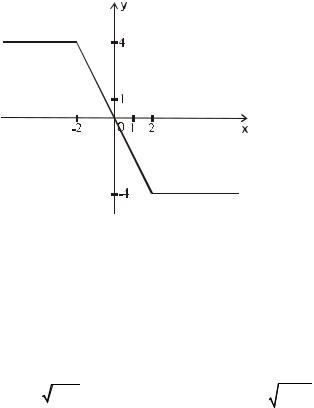
2.Отобразим построенный график симметрично оси 0 y , получим искомый график.

y = x + 1 −1.

Воспользуемся определением модуля, получим:

x + 1 −1, e x + 1 ≥ 0 x, e x ≥ −1

y = −x −1 −1, e x +1 < 0 = − x − 2, e x < −1.

Строим график полученной функции.

y = x − 2 − x + 2 .

Вновь воспользуемся определением модуля, получим:

Краткий курс школьной математики			73

− x + 2 + x + 2, e x < −2		4, e x < −2

y = − x + 2 − x − 2, e − 2	≤ x ≤ 2	= −2x, e − 2	≤ x ≤ 2 .

x − 2 − x − 2, e x > 2		−4, e x > 2

Строим график полученной сложной функции.

Упражнения для самостоятельного решения

p 1

y = −

−1 ;

p 7

y =

+1 ;

x + 2

p 2

y =

x + 3

;

p 8

x + 3

y =

;

x − 3

p 3

p 9

;

y =

x + 1

;

y =

+ 1

p 4

p 10

1 2

y =

x −1

x +1

;

y = 2

x −

;

p 5

y = − ( x + 2)3 − 2 ;

p 11

y =

−1 ;

( x − 2)2

p 6

p 12

y =

x +1

y =

−1

( x − 2)2

74	В.А.Битнер

Тема XIII. Квадратный трехчлен. Выделе- ние полного квадрата. Квадрат- ные уравнения. Разложение квадратного трехчлена на ли- нейные множители.

(1)Квадратный трехчлен. Выделение полного квадрата.

o 1 Выражение вида ax2 + bx + c , где a, b, c R, a ≠ 0 , называется квадратным трехчленом.

Выделим из квадратного трехчлена в общем виде полный квадрат:

ax2 + bx + c = a x

2 +

= a

+ 2 x

−

2a 4a2

4a2

b2 − 4ac

− 4ac

= a

x +

−

= a x +

−

p 1

Выделить

полный

квадрат

из

квадратного

трехчлена

+ 3x + 1 = 2

x +

+ 2x

−

4 16

16 2

3 2

= 2

x +

−

= 2 x

−

;

p 2

− 4x − 2 =

−

x −

− 2x

−

3 9

9 3

2 2

= 3

x −

−

= 3

x −

−

(2)Квадратные уравнения. Формула корней квадратного уравнения.

o 2	Уравнение вида ax2 + bx + c = 0	(1)
	где a, b, c R, a ≠ 0 , называется квадратным.

Краткий курс школьной математики	75

r квадратное уравнение (1), разделим обе части уравнения на	a ≠ 0 ,

получим: x2 + b x + c = 0 , и выделим в левой части уравнения полный

b 2

− 4ac

b 2

b2 − 4ac

квадрат:

x +

−

= 0 , далее имеем:

x +

откуда x +

= ±

b2 − 4ac

, где b2 − 4ac ≥ 0 .

x =

−b ±

b2 − 4ac

, где

D = b2 − 4ac ≥ 0 - дискриминант (различитель -

лат.)

1.Итак, если D > 0 , то квадратное уравнение (1) имеет 2 действительных различных корня

	x		=	−b ± D				(2)

	1,2				2a

2.	e D = 0 , то уравнение (1) имеет 2 действительных равных корня
	x1	= x2			= −	b	.

						2a
3.	e D < 0 , то уравнение (1) не имеет действительных корней.

(3)Неполные квадратные уравнения

r квадратное уравнение ax2 + bx + c = 0 , где a, b, c R, a ≠ 0 .

e b = 0 , то имеем ax2 + c = 0

(3)

x2 = −

и x = ±

−

, где

≥ 0 ;

1,2

e c = 0 , то имеем ax2 + bx = 0

(4)

x (ax + b ) = 0 , откуда x = 0, x

= −

;

e b = c = 0 , то имеем ax2

= 0

(5)

и x R .

Уравнения вида (3), (4) и (5) называются неполными квадратными уравнениями.

76	В.А.Битнер

(4)Формулы четного коэффициента

e в уравнении (1) второй коэффициент b = 2k - четное число (k Z ) ,

то

уравнение принимает

вид

ax2 + 2kx + c = 0 и

D = 4k 2 − 4ac , где

k =

, тогда

= k 2 − ac =

− ac и из формулы (2) при

> 0 имеем

(−k ±

)

−

k 2 − ac

−2k ±

− 4ac

x1,2

2 a

−

Итак, x =

, где

− ac

(6)

1,2

Формулы (6) называются формулами четного коэффициента.

(5)Особые случаи решения квадратных уравнений

t 1	e в квадратном уравнении ax2 + bx + c = 0 выполняется условие
	a + b + c = 0 , то x1 = 1, x2 =			c	.
	a + b + c = 0 , то x1 = 1, x2 =				.
				a
t 2	e для квадратного уравнения выполняется условие a − b + c = 0 ,
t 2
	то x1 = −1, x2 = −	c	.
	то x1 = −1, x2 = −		.
		a

Верны и обратные теоремы.

(6)Приведенные квадратные уравнения. Теорема Виета для приведенного квадратного уравнения и для квадратного уравнения в общем виде.

o 3 Квадратное уравнение вида x2 + px + q = 0 (7), где p, q R , называется приведенным квадратным уравнением (старший коэффициент равен 1).

Краткий курс школьной математики	77

te x1 и x2 - корни приведенного квадратного уравнения

Виета	(7), то выполняются соотношения: x1	+ x2 = − p .
(прямая)	(7), то выполняются соотношения: x1	+ x2 = − p .
	x1	x2 = q

te для некоторых постоянных p и q существуют числа

Виета	(об-		удовлетворяющих соотношениям x1 + x2 = − p ,
ратная)	x и	x ,	удовлетворяющих соотношениям x1 + x2 = − p ,
	1	2	x1 x2 = q
			x1 x2 = q
	то	x1 и	x2 являются корнями приведенного квадратного
	уравнения x2 + px + q = 0 .

Обобщенная теорема Виета.

(7)Разложение квадратного трехчлена на линейные множите- ли.

o 4	Значение	x = x называется	корнем		квадратного трехчлена
		0
	P ( x ) = ax2 + bx + c , если P ( x		) = ax 2	+ bx + c = 0 .
		0	0		0

Как и квадратное уравнение, квадратный трехчлен может иметь 2 действительных различных или 2 действительных равных корня, или не иметь действительных корней.

te x1 и x2 - корни квадратного трехчлена, то ax2 + bx + c = a ( x − x1 ) ( x − x2 ) .

z	e x = x , то ax2		+ bx + c = a ( x − x )2 .
	1	2	1

78	В.А.Битнер

Решение уравнений.

Решить квадратные уравнения и сводящиеся к ним.

p 1

p 2

2x2 + 5x −1 = 0 .

Решение:

D = 25 + 8 = 33, x =

−5 −

; x

−5 +

± 33

Ответ:

−5

x3 − 5x2 + 6x = 0 .

Решение:

= 0

+ 6) = 0

x1 = 0

x (x

− 5x

− 5x + 6

= 2 (по теореме Вие-

= 0

= 3

та).

Ответ: {0; 2; 3} .

3x2 − 2x −1 = 0 .

Решение:
Так как 3 − 2 −1 = 0 , то x				= 1; x = −		1		.
Так как 3 − 2 −1 = 0 , то x				= 1; x = −				.
			1	2		3
						3
Ответ: −	1	;1 .
Ответ: −		;1 .
	3
7 x2 + 4x − 3 = 0 .
Решение:
Так как 7 − 4 − 3 = 0 , то x				= −1; x =			3		.
Так как 7 − 4 − 3 = 0 , то x				= −1; x =					.
			1		2	7
						7
Ответ: −1;		3	.
Ответ: −1;			.
		7

4x2 − 8x + 1 = 0 .

Решение:

По формуле четного коэффициента D = 16 − 4 = 12 , 4

Краткий курс школьной математики	79

p 8

x =

4 − 12

4 − 2 3

2 − 3

; x =

2 + 3

−

2 +

Ответ:

;

x4 − 5x2 + 4 = 0 - биквадратное уравнение.

Решение:

Решить данное уравнение как квадратное

относительно

x2 ,

тогда по t Виета (x

2 )

= 1, (x2 )

= 4 и x

= ±1, x

= ±2 .

1,2

3,4

Ответ: {±1; ±2} .

x3 − 27

= 27 .

x − 3

Решение:

( x − 3)(x2 + 3x + 9)

+ 3

= 27

+ 9 = 27

−18 = 0 .

x − 3

x − 3 ≠ 0

≠ 3

По t Виета из квадратного уравнения в системе x1 = −6, x2

= 3 ,

но x ≠ 3 .

Ответ: {−6} .

x2 + x − 5

= 4 .

+ x − 5

Решение:

Введем замену

x2 + x − 5

= y ,

получаем

y +

= 4 , где y ≠ 0 .

y 2 − 4 y + 3 = 0 , по t Виета y

= 3, y

= 1.

a)x2 + x − 5 = 3 x2 + x − 5 = 3x, x ≠ 0

x2 − 2x − 5 = 0 по формуле четного коэффициента

x1,2	= 1 ±		6 ;
b)		x2 + x − 5			= 1 x2 + x − 5 = x, x ≠ 0
b)					= 1 x2 + x − 5 = x, x ≠ 0
		x
x2
x2	= 5, x		= ± 5				;
	3,4
Ответ: {1 ±						±			} .
Ответ: {1 ±				6;		±		5	} .

80	В.А.Битнер

p 9

p 10

p 11

x ( x + 3) ( x + 2) ( x + 5) = 72 .

Решение:

Перегруппируем сомножители и преобразуем полученное уравнение: (( x + 3) ( x + 2))(( x + 5) x ) = 72 ,

(x2 + 5x + 6)( x2 + 5x ) = 72 , введем замену

x2 + 5x = y , получим уравнение ( y + 6) y = 72 ,

y2 + 6 y − 72 = 0 , по t Виета y1 = −12, y2 = 6 .

a)x2 + 5x = −12, x2 + 5x + 12 = 0, D = 25 − 48 < 0, ;

b)x2 + 5x = 6, x2 + 5x − 6 = 0 , так как 1 + 5 − 6 = 0 , то

x1 = 1, x2 = −6 .

Ответ: {−6;1} .

4x2 + 12x + 12 + 42 = 47 .

Решение:

Перегруппируем слагаемые

дем замену x + 1 = y , тогда x

ние 4 ( y 2 − 2) +12 y − 47 = 0 .

4 x2

x2 +

+	1	+12 x +		1	= 47 и вве-
	x2
				x
1	= y	2 − 2 ,	получаем уравне-
2

4 y 2 +12 y − 55 = 0 ,															по		формуле			четного					коэффициента
	D	= 36 + 220 = 256, y =														−6 −16		= −	11	; y			=	−6 +16	=		5	.
		= 36 + 220 = 256, y =																= −		; y	2		=		=			.
4														1		4			2		2		4		2
4																4			2				4		2

a)		x +	1		= −				11			, 2x		2 + 11x + 2 = 0 . x						=		−11 ± 105				;
a)		x +			= −							, 2x		2 + 11x + 2 = 0 . x						=						;
			x						2										1,2				4
			x						2														4
b)		x +	1	=			5	, 2x2 − 5x + 2 = 0 x											2 − 2		1		x + 1 = 0 ,			по t Виета
b)		x +		=				, 2x2 − 5x + 2 = 0 x											2 − 2				x + 1 = 0 ,			по t Виета
			x				2														2
		x = 2, x =									1		.
		x = 2, x =											.
		3					4		2
									2
										−11 ±
														105
Ответ:					1	; 2;								105			.
Ответ:						; 2;											.
			2						4

x2 + x + 3x − 5 = 0 .

<<< < Предыдущая 1 2 3 4 5 6 78 / 428 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.07.2019400.64 Кб4bestref-201996.rtf
#
12.03.20152.74 Mб10BhagavatGita_kak_ona_est.pdf
#
16.04.201995.65 Кб3Bilety_dlq_ekzamena_po_kursu_Socialogiq_i_psiho....docx
#
25.09.2019173.57 Кб3Bilety_IGA_po_190604TA4.doc
#
19.09.2019507.9 Кб7Biologia.doc
#
12.03.20156.54 Mб83Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki.pdf
#
08.09.2019652.29 Кб4biznes_plan_po_Petrulevich.doc
#
22.03.201663.12 Кб4breaking.pdf
#
12.03.2015931.33 Кб9Broshyura (1).doc
#
12.03.2015826.37 Кб7Broshyura.doc
#
23.11.2019823.3 Кб1Broshyura.doc