Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

6.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 426 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Краткий курс школьной математики	51

Числовая прямая разбивается нулями модулей на три промежутка. Решим неравенство на каждом из этих промежутков.

x <

x ≤ −5 ;

≤ −5

−2x +1 + x − 2 ≥

≤ x ≤ 2

≤ x

≤ 2

;

2x −1 + x − 2 ≥ 4

≥

x > 2

x ≥ 3 .

2x −1 − x + 2 ≥ 4

≥ 3

Ответ: (−∞; −5] [3; +∞ ) .

Упражнения для самостоятельного решения.

Решить неравенства, системы и совокупности неравенств.

p 1

x −

x + 4

3x −1

< 3 ;

p 2

x −1

−

2 x + 3

< 2 −

x + 5

2 ;

1 −

x + 5

4 − x

< 3x −

x + 1

p 3

3x − 4 ≤ 8x + 6

2x −1 > 5x − 4 ;

11x − 9 ≤ 15x + 3

p 4

7 − x

− 3

3 + 4x

− 4

;

x + 5 (4 − x ) > 2 (4 − x )

52	В.А.Битнер

2 x + 7 ≤ 3 ; x − 6 > 2 ; 3 + x ≥ x ;

x + x + 3 < 5 .

Ответы:
p 1	(−∞; 2) ;
p 2	7	1
		;1	;

	9	5
p 3	[−2;1) ;
p 4	(−∞; +∞ ) ;
p 5	[−5; −2] ;
p 6
p 7	(−∞; 4) (8; +∞ );
p 8	(−4;1) .

Тема XI. Некоторые вопросы теории функ- ций.

(1)Определение функции, функциональная символика, область определения и множество значений функции.

o 1	Если каждому значению	некоторой	переменной величины
	x X соответствует единственное значение переменной y Y ,
	то говорят, что задана	функция и	пишут: y = f ( x ) или
	y = ϕ ( x ), y = g ( x ) и т.д.

Причем независимая переменная x называется аргументом (arg.), а зависимая переменная величина y - функцией, f - это совокупность

Краткий курс школьной математики	53

операций над arg x , чтобы получить функцию y , аналогично для ϕ , g и т.д.

Множество X называется областью определения функции и обозначается D ( y ) , а множество Y - областью изменения или множеством зна-

чений функции и обозначается E ( y ) .

(2)График функции.

o 2 Множество точек ( x; y ) координатной плоскости таких, что y = f ( x ) , x D ( y ) , y E ( y ) , называется графиком функции

y = f ( x ) . Обозначается график Г .

Можно записать определение графика функции f ( x ) только с помо-

щью символов:

Гf = {( x; y ) | y = f ( x ) , x D ( y ) , y E ( y )} .

(3)Четность и нечетность функции.

o 3	Функция y = f ( x ) называется четной, если x и − x D ( y ) и при
	этом f (− x ) = f ( x ) .

Очевидно, что график четной функции симметричен оси Oy .
o 4	Функция	y = f ( x ) называется нечетной, если x и − x D ( y ) и

	при этом	f (− x ) = − f ( x ) .

Очевидно, что график нечетной функции симметричен началу координат.

z Надо помнить, что бывают функции ни четные, ни нечетные.

p 1 Исследовать функцию на четность. f ( x ) = x2 −1 .

Имеем: x и − x D ( y ) = R и f (− x ) = (− x )2 −1 = x2 −1 = f ( x )-

54	В.А.Битнер

четная функция.

f ( x ) = x3 .

Имеем:	x и − x D ( y ) и f (− x ) = (− x )3 = −x3 = − f ( x ) . Следова-
тельно,	функция f ( x ) - нечетная.

f ( x ) = x	2 − 2 x − 3 . Имеем x и − x D ( y ) , но
f (− x ) = (− x )2 − 2 (−x ) − 3 = x3 + 2x − 3 ≠ f ( x ) ≠ − f ( x ) , то есть
функция		f ( x ) - ни четная, ни нечетная.

f ( x ) =		x . Имеем, e x D ( y ) = [0; +∞ ) , то − x D ( y ) и функ-

ция f ( x ) - ни четная, ни нечетная.

(4)Точки пересечения графика с осями координат.

Точка (0; f (0)) - точка пересечения графика с осью ординат, ее может не быть или быть не более одной.

Точки ( x1 ; 0) , ( x2 ; 0) , ( x3 ; 0)... - точки пересечения графика с осью абс-

цисс или нули функции. Их может не быть или быть одна, две, три и более.

(5)Интервалы знакопостоянства или знаки функции.

Это те значения x D ( y ) , при которых y > 0 и те значения x D ( y ) ,

при которых y < 0 .

(6)Монотонность (возрастание и убывание) функции.

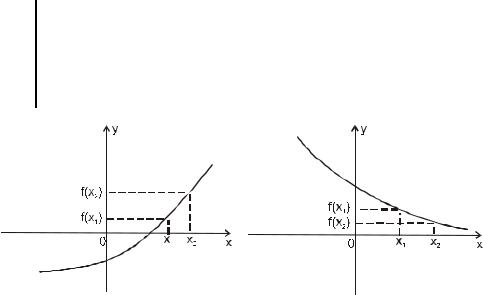
o 5 Функция y = f ( x ) называется возрастающей на числовом мно-

жестве I D ( y ) , если для любых значений x1 , x2 I таких, что x1 < x2 , выполняется условие f ( x1 ) < f ( x2 ) или

( x1 > x2 ) ( f ( x1 ) > f ( x2 )) - см. рис.1

Краткий курс школьной математики	55

o 6 Функция y = f ( x ) называется убывающей на числовом множе-

стве I D ( y ) , если для любых значений x1 , x2 I таких, что x1 < x2 , выполняется условие f ( x1 ) > f ( x2 ) или

( x1 > x2 ) ( f ( x1 ) < f ( x2 )) - см. рис.2

рис.1 рис.2

Возрастающие и убывающие функции называются монотонными.

(7)Экстремумы (максимумы и минимумы) функции.

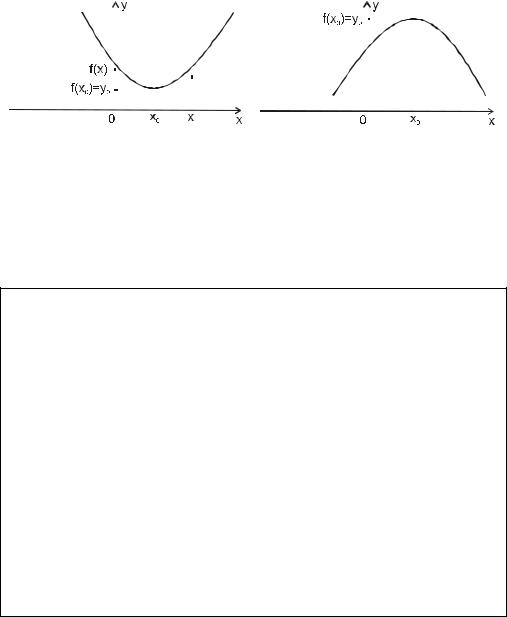
o 7	Тч. x I называется точкой минимума (min .) функции f ( x ) на
		0
	I ,	если для x I , где I D ( y ) , выполняется неравенство
	f ( x0 ) < f ( x ) . Причем			y0 = f ( x0 ) называется минимумом
	функции f ( x ) на I .

Обычно пишут ymin = f ( x0 ) - см. рис.3
o 8	Тч.	x	I называется	точкой	максимума (max .) функции
o 8	Тч.	x	I называется	точкой	максимума (max .) функции
		0
	f ( x ) на		I , если для x I , где		I D ( y ) , выполняется нера-
	венство		f ( x0 ) > f ( x ) .	Причем	y0 = f ( x0 ) называется макси-
	мумом функции f ( x ) на I .

56	В.А.Битнер

Обычно пишут ymax = f ( x0 ) - см. рис.4

рис.3

рис.4

(8)Схема исследования функции.

1.D ( y ) ;

2.Четность, нечетность (симметричность графика оси 0 y или началу координат);

3.Периодичность функции - будет рассмотрена в теме XIX;

4.Точка пересечения графика с осью 0 y , то есть это точка (0; f (0)) ;

5.Нули функции;

6.Знаки функции;

7.Монотонность (возрастание, убывание);

8.Экстремумы (min, max);

9.E ( y ) ;

10.График функции.

Краткий курс школьной математики	57

Тема XII. Некоторые алгебраические функции

иих графики.

(1)Линейная функция.

o 1

Функция вида

y = kx + b , где k , b R, k ≠ 0 , называется линей-

ной.

e b = 0 , то имеем

y = kx

- прямопропорциональная зависимость.

r график прямопропор-

циональной зависимости в

зависимости от знака ко-

эффициента k - см. рис.1

и рис.2

а) k > 0

График расположен в I и III

координатных четвертях

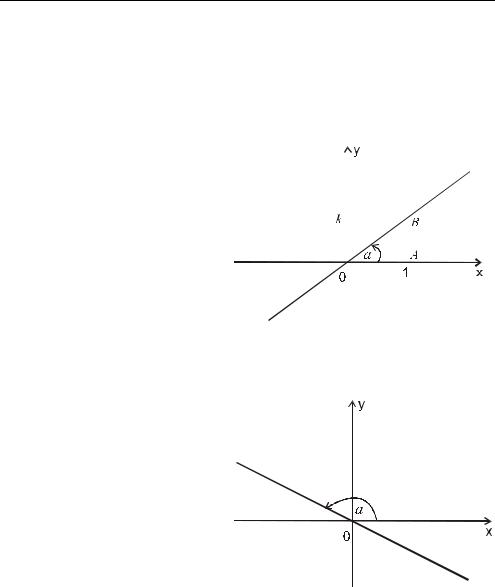
(квадрантах). r AOB - угол,

составленный графиком

функции y = kx с положи-

тельным направлением оси

рис.1

0 x , то tgα =

- угол

OA 1

острый.

	б) k < 0
	График расположен во II и IV
	координатных четвертях,
	функция убывает, угол
	α тупой.
	Геометрический смысл угло-
	вого коэффициента k .	рис.2
	k = tgα , где α - угол графика	рис.2
	k = tgα , где α - угол графика
	функции y = kx с положи-

58				В.А.Битнер

тельным направлением оси 0x .
2) e b ≠ 0 , то имеем				y = kx + b , график этой функции получается из
графика функции				y = kx параллельным переносом вдоль оси 0 y на
b единиц.
Точки (0; b ) и	−	b	; 0	- точки пересечения графика с осями координат

		k

- см. рис.3 и рис.4.

рис.3	рис.4

Геометрический смысл коэффициента k для функции y = kx + b тот же, то есть k = tgα .

3) Уравнения прямых, имеющих в алгебре специальное название:

1. y = x - уравнение биссектрисы координатных углов I и III четверти; 2. y = − x - уравнение биссектрисы координатных углов II и IV чет-

верти;

3.y = 0 - уравнение оси 0x ;

4.x = 0 - уравнение оси 0 y ;

5.y = b - уравнение прямой, параллельной оси 0x и отсекающей по оси 0 y b единиц;

6.x = m - уравнение прямой, параллельной оси 0 y и отсекающей по оси 0x m единиц;

4) Различные виды уравнений прямых.

Краткий курс школьной математики	59

1.Каноническое уравнение прямой: ax + by + c = 0 ;

2.уравнение прямой с угловым коэффициентом: y = kx + b ;

3.уравнение прямой с угловым коэффициентом k , проходящей через заданную точку ( x0 ; y0 ) :

y − y0 = k ( x − x0 )

(1)

4. уравнение прямой, проходящей через две заданные точки ( x1 ; y1 ) и

( x2 ; y2 ) :

x − x1

y − y1

(2)

x2 − x1

y2 − y1

5) Условия параллельности и перпендикулярности двух прямых.

n уравнение прямой a1 имеет вид:

y = k1 x + b1 , а уравнение прямой

a2 имеет вид:

y = k2 x + b2 .

e k1 = k2 , то a1 a2 и обратно: e a1 a2 , то k1 = k2 .

e k k

= −1 , то есть k

= −

, то a a

и обратно.

p 1

Графики прямых y = 2x + 1и y = 2x − 3 параллельны.

p 2

Графики прямых y = 2x + 1и y = −

x −1 перпендикулярны.

Решение упражнений.

p 1

Исследовать функцию y = −

x .

D ( y ) = R ;

f (

− x ) = −

(− x ) = −

( x ) , функция нечетная, ее

−

= − f

график симметричен началу координат;

3.(0; 0) - точка пересечения графика с осями координат;

4.y > 0, e x < 0 и y < 0, e x > 0

5.Так как k = − 1 < 0 , то функция монотонно убывает на R ;

60	В.А.Битнер

p 2

p 3

p 4

6.Экстремумов нет;

7.E ( y ) = R ;

8.График. 1; − 1 -

дополнительная точка.

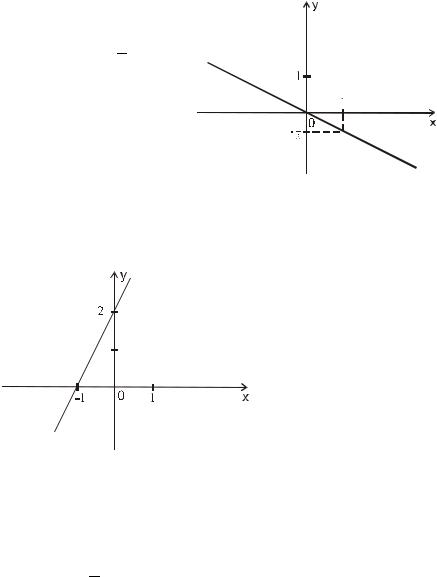
Построить график функции y = 2x + 2 .

Для построения прямой достаточно двух точек, удобнее выбрать точки (0; 2) и (−1; 0) пересечения с осями 0 y и 0x .

Составить уравнение прямой, проходящей через 2 заданные точки (1; −2) и (−1; 3) .

Решение:

Из (2) имеем:	x −1	=	y + 2	y + 2 = −	5	x + 1 y = −	5	x −1.

	−1 −1 3 + 2			2		2

Ответ: y = − 5 x −1 . 2

Составить уравнение прямой, проходящей через точку (1; −1) и

a)параллельной прямой y = −3x + 1 ;

b)перпендикулярной этой прямой. Решение:

a) Из условия параллельности двух прямых имеем k1 = k2 = −3 ,

<<< < Предыдущая 1 2 3 4 56 / 426 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.07.2019400.64 Кб4bestref-201996.rtf
#
12.03.20152.74 Mб10BhagavatGita_kak_ona_est.pdf
#
16.04.201995.65 Кб3Bilety_dlq_ekzamena_po_kursu_Socialogiq_i_psiho....docx
#
25.09.2019173.57 Кб3Bilety_IGA_po_190604TA4.doc
#
19.09.2019507.9 Кб7Biologia.doc
#
12.03.20156.54 Mб83Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki.pdf
#
08.09.2019652.29 Кб4biznes_plan_po_Petrulevich.doc
#
22.03.201663.12 Кб4breaking.pdf
#
12.03.2015931.33 Кб9Broshyura (1).doc
#
12.03.2015826.37 Кб7Broshyura.doc
#
23.11.2019823.3 Кб1Broshyura.doc