Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

6.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 425 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Краткий курс школьной математики	41

(2)Свойства числовых неравенств.

1o	(симметричности) e a > b, то b < a ;
2o	(транзитивности) e a > b и b > a, то a > c ;
3o	e a > b, то a ± c > b ± c ;

sКакой-либо член неравенства можно перенести из одной его части в другую с противоположным знаком, оставив при этом без изменения знак неравенства.

4o	e a > b и c > 0, то ac > bc и		a		>		b		;

			c c
5o	e a > b и c < 0, то ac < bc и	a		<		b		.

(3)Действия с неравенствами.

t 1 Два неравенства одинакового смысла можно почленно складывать, оставляя тот же знак.

То есть, e a > b и c > d , то a + b > c + d , или, если e a < b и c < d , то a + b < c + d .

t 2 Два неравенства противоположного смысла можно почленно вычитать, оставляя знак уменьшаемого неравенства.

То есть, e a > b и c < d , то a − c > b − d , или, e a < b и c > d , то a − c < b − d .

t 3 Два неравенства одинакового смысла с положительными частями можно почленно умножать, оставляя тот же знак.

То есть, e a > b > 0 и c > d > 0, то ac > bd .

s1		ea > b > 0 и n N , то an > bn .
s2		e an > bn где n N , a > 0, b > 0, то a > b .
s2		e an > bn где n N , a > 0, b > 0, то a > b .

42 В.А.Битнер

Замечания

t 1 можно обобщить на случай

n неравенств, то есть, если

a > b , a

> b ,..., a

> b , то a + a + ... + a

> b + b + ... + b .

t 33можно обобщить на случай

n неравенств, то есть, если

a > b > 0, a

> b

> 0,..., a

> b

> 0,

то a a ...a

> b b ...b .

1 2

(4)Числовые промежутки.

1.Числовая прямая, пишут: (−∞; +∞ ) или R .

2.Числовые полупрямые или числовые лучи, пишут:

(−∞; a ) или x < a, (a; +∞) или x > a - строгие неравенства;

(-∞; a] или x ≤ a,[a; +∞ ) или x ≥ a - нестрогие неравенства.

3.Числовой отрезок или сегмент, пишут: [a; b] или a ≤ x ≤ b - двойное нестрогое неравенство.

4.Числовой интервал, пишут: (a; b) или a < x < b - двойное строгое неравенство.

5. Числовые полуинтервалы или полусегменты, пишут: [a; b ) или a ≤ x < b , (a; b] или a < x ≤ b - двойные неравенства.

(5)Доказательство неравенств.

Для доказательства неравенств обычно используют один из следующих двух путей:

1.Равносильными преобразованиями получают из исходного неравенства очевидное неравенство, то есть неравенство одного из следующих видов:

a2 ≥ 0, (a − b)2 ≥ 0, −a2 −1 < 0, (a + b + c )2 + 2 > 0 и им подобных. Тем

самым исходное неравенство доказано.

2.Из одного, двух и более очевидных неравенств равносильными преобразованиями, используя свойства и теоремы о действиях с неравенствами, свойства модуля, теорему о среднем арифметическом и среднем геометрическом, получают исходное неравенство. Тем самым оно доказано.

Краткий курс школьной математики	43

tСреднее арифметическое n неотрицательных чисел

о среднем

не меньше среднего геометрического этих чисел,

арифметическом

где n N . То есть

a1 + a2 + ... + an

≥ n a a

... a .

среднем геомет-

рическом

a1 + a2

Докажем теорему для n = 2 , то есть докажем, что

≥ a a

или

a + b ≥ ab , где a ≥ 0, b ≥ 0 . Умножим обе части неравенства на поло- 2

жительное число и перенесем 2ab влево с противоположным знаком,

получим a + b − 2ab ≥ 0 (a − b )2 ≥ 0 - очевидное неравенство. d

zМетодом математической индукции теорему можно доказать и для n чисел.

Упражнения на доказательство неравенств.

Доказать неравенства:

a	2	− a + 1 > 0
Доказательство:
	2		1		1		3		1	2		3
a	2	− 2 a		+		+		> 0 a −			+		> 0	- очевидное неравен-
a		− 2 a		+		+		> 0 a −			+		> 0	- очевидное неравен-
			2		4		4		2			4

ство.

Доказать, что правильная дробь увеличивается, если к числителю и знаменателю этой дроби прибавить по единице. Доказательство.

Пусть дана правильная дробь m , где m, n N , m < n . n

Докажем, что m +1 − m > 0 .

	n +1	n
Имеем:	mn + n − mn	− m	> 0	n − m	> 0 , но

	n (n + 1)			n (n +1)

n (n +1) > 0 и n − m > 0 n > m , что соответствует условию. d

44	В.А.Битнер

p 3

p 4

a4 + b4 − a3b − ab3 ≥ 0

Доказательство:

a3 (a − b ) − b3 (a − b ) ≥ 0 (a − b ) (a3 − b3 ) ≥ 0

(a − b)2 (a2 + ab + b2 ) ≥ 0, но (a − b )2 ≥ 0 - очевидное неравен-

ство, и легко доказать, что a							2 + ab + b2 ≥ 0 . Перепишем это не-
равенство в виде
a2 + 2a	b		b2		3b2			b	2	3b2
		+		+		≥ 0 a	+		+		≥ 0 - очевидное нера-
		+		+		≥ 0 a	+		+		≥ 0 - очевидное нера-
	2		4		4			2		4

венство. d

(a + 1)(b + 1)(c +1) ≥ 8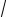abc , где a ≥ 0, b ≥ 0, c ≥ 0 .

Доказательство:

Рассмотрим очевидные неравенства:

(a −1)2 ≥ 0, (b −1)2 ≥ 0, (c −1)2 ≥ 0 или, что то же самое,

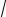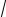a +1 ≥ 2a , b + 1 ≥ ab , c +1 ≥ 2c .

Перемножим положительные левые и правые части этих нера-

венств, получим: (a + 1) (b +1) (c +1) ≥ 8abc . d

a2 + b2 + c2 + 3 ≥ 2 (a + b + c ) .

Доказательство:

Рассмотрим очевидные неравенства:

a2 + 1 ≥ 2a, b2 + 1 ≥ 2b, c2 +1 ≥ 2c , сложим левые и правые части этих неравенств, получим: a2 + b2 + c2 + 3 ≥ 2 (a + b + c ) .d

	1		1
(a + b )		+		≥ 4,	где a > 0, b > 0 .
(a + b )		+		≥ 4,	где a > 0, b > 0 .
a			b

Доказательство:

По теореме о среднем арифметическом и среднем геометриче-

a + b

или a + b ≥ 2

≥

ском

≥ ab ,

≥

a b

Перемножим левые и правые части последних двух неравенств,

получим: (a + b )	1	+	1	≥ 4 . d

a			b

Краткий курс школьной математики

p 7

(a2 + b2 + c2 + d

2 )

≥ 16 , где

d 2

a ≠ 0, b ≠ 0, c ≠ 0, d ≠ 0 .

Доказательство:

По теореме о среднем арифметическом и среднем геометриче-

a2 + b2 + c2 + d 2

≥

4 a2b2c2 d

ском

≥ 4

. Умножим обе части каж-

дого неравенства на 4 и перепишем левые и правые части по-

лучившихся неравенств, получим

(a2 + b2 + c2 + d

2 )

≥

d 2

≥ 16 a2b2c2 d

= 16 .d

a b c d

p 8

x −1

x − 2

≥ 1 .

Доказательство:

2 − x

≥ 1 и

Заменим исходное неравенство равносильным

x −1

докажем его.

2 − x

≥

x −1 + 2 − x

= 1 .d

Из свойств модуля имеем:

x −1

p 9

x + 2

x − 5

x − 3

≥ 7 .

Доказательство.

Сначала докажем, что

x + 2

x − 5

≥ 7

x + 2

5 − x

≥ 7 . Из

x + 2

5 − x

≥

x + 2 + 5 − x

= 7 .

свойств модуля

Но x − 3 ≥ 0 x + 2 + x − 5 + x − 3 ≥ 7 .d

Упражнения для самостоятельного решения.

Доказать неравенства:

p 1	m4 + m3n + mn3 + n4 ≥ 0 ;
p 2	a2 + b2 + c2 + 2 > ab + ac + bc .

В.А.Битнер

Указание: предварительно умножить обе части неравенства на

p 3

(a + b + c )

≥ 9, где a ≠ 0, c ≠ 0, d ≠ 0 ;

a b

p 4

x + 1

x − 2

x + 3

x − 4

≥ 10 ;

p 5

x + 5

x − 5

x −1

≥ 5 .

(6)Решение линейных неравенств, систем и совокупностей линейных неравенств с одной переменной.

o 1 Линейными называются неравенства вида

ax > b, ax < b, ax ≥ b, ax ≤ b, где a, b R, a ≠ 0 .

o 2 Решением неравенства с одной переменной называется множество таких значений переменной, которые обращают его в верное числовое неравенство.

e a > 0 ,

то

решение

неравенства

ax > b имеет

вид

x >

(или

; +∞ ).

e a < 0 ,

то

решение

неравенства

ax > b имеет

вид

x <

(или

x −∞;

e a = 0 ,

то неравенство ax > b принимает вид 0 x > b , то есть оно

не имеет решения при b ≥ 0 и верно при любых x R , если b < 0 .

o 3 Два неравенства называются равносильными, если множества их решений совпадают.

Основная идея решения неравенства заключается в замене неравенства более простым, но равносильным данному. При этом используются уже рассмотренные основные свойства неравенств и теоремы о действиях с неравенствами и следствия из них.

Краткий курс школьной математики	47

Несколько неравенств с одной переменной могут образовывать систему или совокупность.

Решением системы неравенств с одной переменной называются значения переменной, при которых каждое из неравенств обращается в верное числовое неравенство. То есть решением системы неравенств с одной переменной является пересечение множеств решений каждого неравенства системы.

Решением совокупности неравенств с одной переменной называются значения переменной, при которых хотя бы одно из неравенств обращается в верное числовое неравенство. То есть решением совокупности неравенств с одной переменной является объединение множеств решений каждого неравенства совокупности.

Решение неравенств, содержащих переменную под знаком модуля, находится аналогично решению уравнений подобного рода (см. IX-(2)- p 7).

Решить неравенства, системы и совокупности неравенств.

p 1

x −

x + 1

x − 3

−

x − 2

Решение:

Умножим обе части неравенства на общий знаменатель 12, по-

лучим 12x − 6 x − 5 > 3x − 9 − 4x + 8 7 x > 5 x >

Ответ:

; +∞

p 2

(3x −1) − 50x +1 < 2 ( x + 4)

51x −17 − 50x + 1 < 2 x + 8

−11x < 11x

+10

−11x −11x

< 10 −12

−x < 24

x > −24

−22x

< −2

x >

48	В.А.Битнер

p 6

x > 1

Ответ:

; +∞

3x −1

3x ≤ 1

x ≤

12x − 9x + 3 ≤ 4

2x −

≤

3 .

− 2 > 1

+ 4x

6 x > 3

x >

10 x

x >

Ответ:

17 (3x −1) − 50 +1 < 2 ( x + 4)

x > −24

12 −11x < 11x +10

x >

Ответ: (−24; +∞)

3x −1

3x ≤ 1

2 x −

≤

x ≤

x >

10 x

− 2 > 1 + 4x

Ответ: −∞;

; +∞ .

x − 3

< 1 .

Решение:

a, ea ≥ 0

1 сп. По определению модуля

x − 3 ≥

x ≥ 3

−a, e a < 0

3 ≤ x < 4 ;

x − 3 < 1

x < 4

x − 3 <

x <

x < 3

2 < x < 3 ;

− x + 3 < 1

−x

< −2

x > 2

Ответ: (2; 4)

2 сп. x − 3 < 1 −1 < x − 3 < 1 −1 + 3 < x < 1 + 3 2 < x < 4 . 3 сп. Из геометрического смысла модуля имеем:

Краткий курс школьной математики	49

p 7

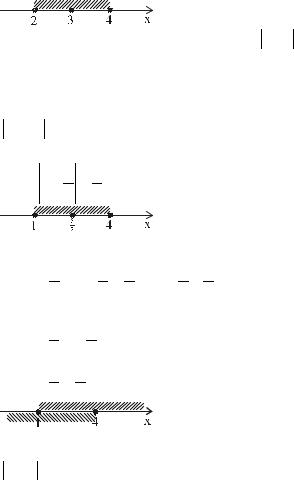
p 8

Точка с координатой 3 - нуль модуля x − 3 .

От точек с координатами 2 и 4 расстояние до точки с координатой 3 равно 1.

Ответ: (2; 4) .

5 − 2 x ≤ 3 .

Решение:

1 сп. x − 5 ≤ 3 (графический)

Ответ: [1; 4] .

2 сп. − 3 ≤ x − 5 ≤ 3 = − 3 + 5 1 ≤ x ≤ 4 . 2 2 2 2 2

3 сп.

a) x − 5 ≥ − 3 x ≥ 1 ;

b)x − 5 ≤ 3 x ≤ 4 ;

Ответ: [1; 4] .

x + 2 > 4

Решение:

1 сп. По определению модуля

	x + 2 < 0				x < −2
a)						x < −6 ;
	− x − 2 > 4				x < −6
	x + 2 ≥ 0			x ≥ −2
b)						x > 2 .
	x + 2 > 4			x > 2
Ответ: (−∞; −6) (2; +∞) .
					x + 2 < −4		x < −6
2 сп.		x + 2	>	4
					x + 2	> 4	x > 2

Ответ: (−∞; −6) (2; +∞) .

50	В.А.Битнер

p 9

p 10

3 сп.

Ответ: (−∞; −6) (2; +∞) .

7 − 3x ≥ 2

Решение: перепишем неравенство в виде:																								x −	7	≥	2
Решение: перепишем неравенство в виде:																								x −		≥
																								3		3
1 сп.
			7														7
	x <												x		<						5
	x <		3										x		<		3				5
a)			3														3	x ≤				;
a)						7						2					5	x ≤			3	;
						7						2					5				3
	− x +								≥				x		≤
						3						3					3
	x ≥			7											7
	x ≥														7
			3										x	≥
b)			3										x	≥		3 x ≥ 3 .
b)			7						2							3 x ≥ 3 .
			7						2					≥ 3
	x −						≥						x	≥ 3
			3						3
Ответ:			−∞;							5			[3; +∞ ) .
Ответ:			−∞;										[3; +∞ ) .
										3
																	7			2			5
													x −					≤ −
													x −					≤ −
2 сп.		x −			7			≥			2						3			3		x ≤
					7						2						3						3 .
																							3 .
			3					3					x −				7		2
			3					3										≥				x ≥ 3


																	3	3
																	3	3
3 сп.

Ответ:			−∞;							5			[3; +∞ ) .
Ответ:			−∞;										[3; +∞ ) .
										3

2 x −1 − x − 2 ≥ 4

Решение:

Нулями модулей являются x = 1 и x = 2 .

<<< < Предыдущая 1 2 3 45 / 425 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.07.2019400.64 Кб4bestref-201996.rtf
#
12.03.20152.74 Mб10BhagavatGita_kak_ona_est.pdf
#
16.04.201995.65 Кб3Bilety_dlq_ekzamena_po_kursu_Socialogiq_i_psiho....docx
#
25.09.2019173.57 Кб3Bilety_IGA_po_190604TA4.doc
#
19.09.2019507.9 Кб7Biologia.doc
#
12.03.20156.54 Mб83Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki.pdf
#
08.09.2019652.29 Кб4biznes_plan_po_Petrulevich.doc
#
22.03.201663.12 Кб4breaking.pdf
#
12.03.2015931.33 Кб9Broshyura (1).doc
#
12.03.2015826.37 Кб7Broshyura.doc
#
23.11.2019823.3 Кб1Broshyura.doc