
Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki
.pdf
Краткий курс школьной математики |
91 |
|
|
2.Отобразим этот график симметрично оси 0 y , получим искомый график.
p 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y = x2 + |
x −1 |
−1 ; |
|
|
|
|
|
|
|||||||||
|
x = 1 - нуль модуля. |
|
|
||||||||||||||
|
При x < 1 y = x2 − x +1 −1 = x2 − x , |
||||||||||||||||
|
при x ≥ 1 y = x2 + x −1 −1 = x2 + x − 2 . |
||||||||||||||||
|
|
|
|
x |
2 |
|
|
x |
|
e x |
|
|
|||||
|
|
|
|
|
|
− |
|
|
|
|
, |
|
|
|
< 1; |
|
|
|
Итак, |
y = |
2 |
|
|
|
|
|
|
|
|
|
|
, строим график данной сложной |
|||
|
|
|
|
x |
+ x − 2, e x ≥ 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
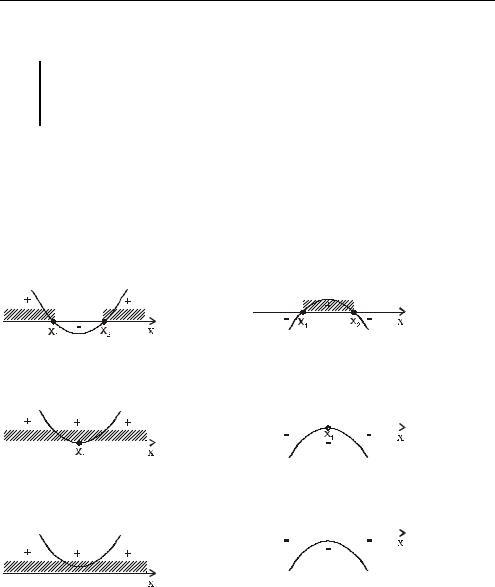
a) Строим график функции y = x2 − x ; |
||||||||||||||||
|
1) |
(0; 0) |
и (0;1) - точки пересечения графика с осями коор- |
||||||||||||||
|
|
динат; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
2) |
|
1 |
; − |
1 |
|
- вершина параболы; |
||||||||||
|
|
|
|||||||||||||||
|
|
2 4 |
|
|
|
|
|
|
|
|
|
|
|||||
|
3) |
дополнительная точка (−1; 2) . |
|||||||||||||||
Выделяем часть графика, где x < 1.
b)Строим график функции y = x2 + x − 2 ;
1)(0; −2) - точка пересечения графика с осью 0 y ;
2)(−2; 0) и (1; 0) - точки пересечения графика с осью 0x ;
3)− 1 ; −2 1 - вершина параболы.
2 4

92 |
В.А.Битнер |
|
|
Выделяем часть графика, где x ≥ 1. Получили искомый график.
Упражнения для самостоятельного решения.
Построить графики функции.
p 1 |
y = 2x2 + x −1; |
||||||||||
p 2 |
y = 3( x −1)( x + 5) ; |
||||||||||
p 3 |
y = 2x2 + x + 1; |
||||||||||
p 4 |
y = 4x2 + 4x + 1 ; |
||||||||||
p 5 |
y = − |
1 |
( x − 2)2 +1 ; |
||||||||
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|||
p 6 |
y = |
|
2 |
+ 2 x − 8 |
|
; |
|||||
|
|
||||||||||
|
|
x |
|
||||||||
p 7 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||||||||
y = x2 + 2 |
x |
− 8 ; |
|||||||||
p 8 |
y = ( x −1)2 ; |
||||||||||
p 9 |
y = x2 −1; |
||||||||||
p 10 |
|
|
|||||||||
y = x2 − |
x + 3 |
− 3 . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Краткий курс школьной математики |
93 |
|
|
Тема XV. Решение квадратных и дробно – линейных неравенств, дробно – рациональных неравенств и нера- венств высших степеней.
(1)Квадратные неравенства.
oНеравенства вида ax2 + bx + c > 0 , ax2 + bx + c < 0 ,
ax2 + bx + c ≥ 0 , ax2 + bx + c ≤ 0 , где a, b, c R, a ≠ 0 , называются
квадратными.
Решим два квадратных неравенства в общем виде
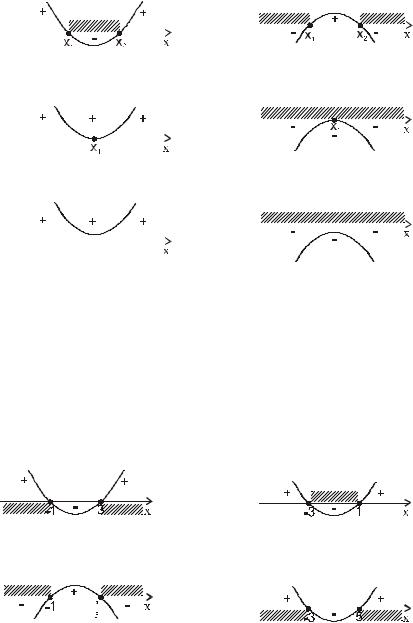
I. |
ax2 + bx + c > 0 |
|
а) a > 0 , |
б) a < 0 , |
|
1. |
D > 0 2 точки пересечения |
1. D > 0 |
x1 и x2
Ответ: (−∞; x1 ) ( x2 ; +∞) |
Ответ: ( x1; x2 ) |
|||
|
2. D = 0 |
|
2. D = 0 |
|
|
точка касания x1 = x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (−∞; x1 ) ( x1; +∞ ) |
Ответ: |
|
3. D < 0 |
|
3. D < 0 |
нет точек пересечения |
|
|
|
|
|
Ответ: (−∞; +∞) или R |
Ответ: |
94 |
В.А.Битнер |
|
|
II.ax2 + bx + c ≤ 0
а) a > 0 , |
б) a < 0 , |
||
1. D > 0 |
1. D > 0 |
||
|
|
|
|
|
|
|
|
Ответ: [x1; x2 ] |
Ответ: (−∞; x1 ] [x2 ; +∞ ) |
||
2. D = 0 |
2. D = 0 |
||
|
|
|
|
|
|
|
|
Ответ: { x1} |
Ответ: R |
||
3. D < 0 |
3. D < 0 |
||
|
|
|
|
|
|
|
|
Ответ: |
Ответ: R |
|
|
Самостоятельно решить в общем виде неравенства: |
|||
III. |
ax2 + bx + c < 0 |
IV. |
ax2 + bx + c ≥ 0 |
Решение упражнений.
Решить неравенства.
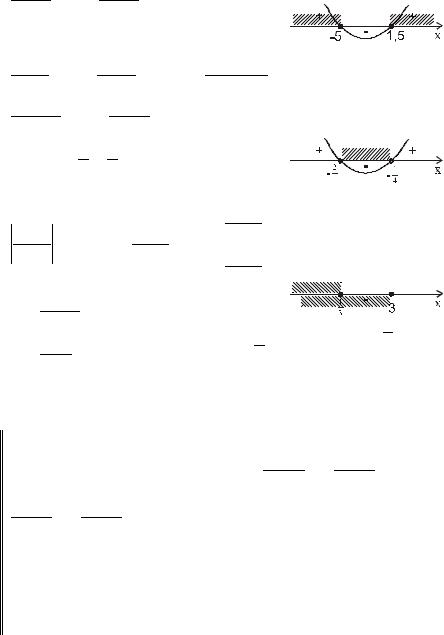
p 1 x2 − 2 x − 3 > 0 ; |
p 22 |
2 x2 + x − 3 ≤ 0 ; |
Ответ: (−∞; −1) (3; +∞ ) |
|
Ответ: [−3;1] |
|||||
p 3 −5x2 − 2 x + 3 < 0 ; |
p 4 |
x2 − 2 x −15 ≥ 0 ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (−∞;1) (0, 6; +∞ ) |
Ответ: (−∞; −3] [5; +∞ ) |

Краткий курс школьной математики |
|
95 |
||||||
|
|
|
|
|
|
|
|
|
p 5 2 x2 + x + 1 > 0 ; |
p 6 |
−9 x2 + 6 x −1 ≥ 0 ; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: R |
1 |
|
|
|
Ответ: |
|
|
|
|
||
|
|
3 |
|
(2)Дробно – линейные неравенства
o 2 |
Неравенства вида |
ax + b |
> 0, |
ax + b |
< 0, |
ax + b |
≥ 0 и |
|
ax + b |
≤ 0 , |
|||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
cx + d |
|
cx + d |
cx + d |
|
cx + d |
||||||||
|
где a, b, c, d R, a ≠ 0, c ≠ 0 , |
называются дробно – |
линейными |
||||||||||||||||
|
неравенствами. К |
|
ним |
сводятся |
и неравенства вида |
||||||||||||||
|
|
ax + b |
> e, |
ax + b |
< e, |
ax + b |
≥ e и |
ax + b |
≤ e , где e R . |
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
cx + d |
|
cx + d |
|
cx + d |
|
|
cx + d |
|
|
|
|
|
|||||
Дробно – линейные неравенства решаются сведением к квадратным, например,
1)ax + b > 0 (ax + b )(cx + d ) > 0 ; cx + d
|
ax + b |
|
|
|
|
|
(ax + b)(cx + d ) ≤ 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
|
|
≤ 0 |
|
|
|
d |
|
|
и т.д. |
|||
cx + d |
|
||||||||||||
|
|
|
|
|
|
x ≠ − |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
p 1 |
|
x − 3 |
> 0 ( x − 3)( x + 2) > 0 |
||||||||||
|
|
|
|||||||||||
|
|
x + 2 |
|
|
|
|
|
|
|
|
|||
|
Ответ: (−∞; −2) (3; +∞) |
||||||||||||
p 2 |
|
2 x + 1 |
|
|
|
(2x +1)(3x − 4) ≤ 0 |
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
≤ 0 |
|
|
4 |
|
|||
|
|
3x − 4 |
|
|
|||||||||
|
|
|
|
|
x ≠ |
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
Ответ: |
−0, 5;1 |
|
|
|
|||
|
|
3 |
|
96 |
В.А.Битнер |
|
|
p3
p4
p 5
(3)
o 3
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
(2x − 3)( x + 5) ≥ 0 |
|
|
|
|
|
|
|
|
||||||||
3 − 2 |
|
|
≤ |
0 |
2 |
|
|
− 3 |
≥ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x + 5 |
|
|
|
|
|
x + 5 |
|
|
|
x |
≠ −5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (−∞; −5) [1, 5; +∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x |
|
> 2 |
|
|
|
x |
|
|
|
− 2 > 0 x − 8x − 2 > 0 |
|
|
|
|
|
|
|
|
|||||||||||||||||
4x + 1 |
|
|
|
|
|
4 x + 1 |
|
|
|
|
4x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
−7 x − 2 > 0 7 x + 2 < 0 (7 x + 2)(4x + 1) < 0 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
4x + 1 |
|
|
|
|
|
4x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ответ: |
− 2 ; − 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
7 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x +1 > −3 |
|
|
|
|
|
|
|
|
|
|||||
3x +1 |
|
|
< 3 −3 < |
3x + 1 |
|
|
x |
− 3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
< 3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 3 |
|
|
3x |
+1 |
< 3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 3 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||
|
6x − 8 > 0 |
|
|
|
|
|
|
x − 3 < 0 |
x < 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
−∞;1 |
. |
|
|||||||||||||||||||
|
|
10 |
|
|
|
|
|
|
|
|
|
3x − 4 > 0 |
x |
|
> |
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
< 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
− 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рациональные неравенства. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Рациональными называются неравенства вида |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
P ( x) > 0, P ( x) < 0, P ( x) ≥ |
0, P ( x) ≤ 0, |
P ( x) |
> |
0, |
P ( x) |
< 0, |
|
|
|||||||||||||||||||||||||||
n |
|
n |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
( x) |
|
|
Q ( x) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
m |
|
|
|
, |
|
|
P ( x) |
|
|
|
|
P ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
≥ |
0, |
|
≤ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Q ( x) |
|
|
|
|
Q ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
m |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
n |
( |
|
) и |
|
m |
( |
|
|
|
) - многочлены соответственно степеней |
n |
и |
|||||||||||||||||||||
|
P |
|
|
x |
|
Q |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
m , то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
P ( x) = a xn + a |
|
|
|
xn −1 +…+ a x + a Q ( x) = b xm + b |
xm−1 |
+… |
|||||||||||||||||||||||||||||
n |
|
|
|
|
|
n |
|
|
|
n |
−1 |
|
|
|
|
|
1 |
0, |
|
m |
|
|
m |
|
|
m−1 |
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…+ b1 x + b0
Рациональные неравенства обычно решаются методом интервалов.

Краткий курс школьной математики |
|
|
|
|
|
|
|
|
|
|
|
97 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Отметим, что неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
P |
( |
x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
( |
x |
) |
|
|
|
|
P ( x) Q ( x) ≥ 0 |
||||
|
|
|
|
P |
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|||||||
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
|
|
> 0 |
n |
( |
|
) |
|
m |
( |
|
|
) |
> 0, |
n |
|
|
|
≥ 0 |
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Q ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
Q ( x) |
|
|
|
|
|
Q ( x) ≠ 0 |
|
|||||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|
|||
Для того, чтобы решить неравенство |
P |
x |
|
|
|
> 0 , необходимо раз- |
||||||||||||||||||||||||
|
n ( |
|
) |
|
Qm ( x) |
|||||||||||||||||||||||||
ложить многочлены |
|
n |
( |
|
|
) и |
|
m ( x) на множители: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P |
|
x |
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P ( x) = (c x − x )k1 (c x − x )k2 |
…(c x − x )kn |
, где c , c ,…, c R , |
|||||||||||||||||||||||||||
|
n |
|
|
1 |
1 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
n |
|
|
|
n |
|
|
|
|
1 |
2 |
n |
|
k , k |
,…, k |
N , а x , x ,…, x - корни уравнения P ( x) = 0 . |
||||||||||||||||||||||||||||
1 |
|
2 |
|
|
n |
|
|
|
1 |
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
||
Рассмотрим метод интервалов на конкретных примерах.
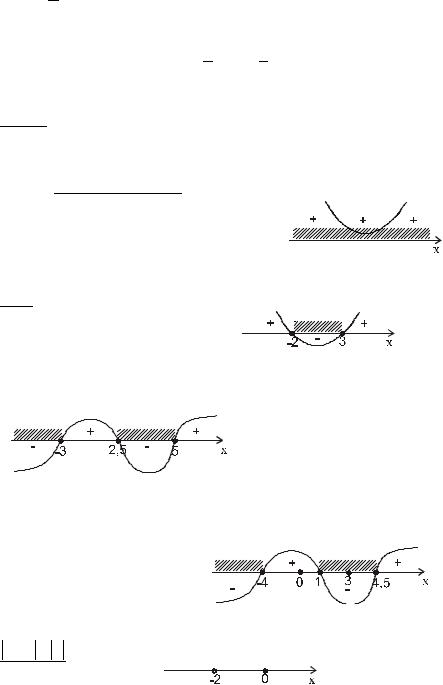
p 1 (1 − 3x )7 (3 − 2x )2 (1 + 3x )3 (2 − x )5 x3 ( x + 2)4 ( x + 3)3 > 0
Решение 1) Найдем нули левой части неравенства, это
x |
= |
1 |
, x |
= |
3 |
, x |
= − |
1 |
, x |
= 2, x |
= 0, x |
= −2, x = −3 |
. Все эти |
|
|
|
|
||||||||||||
1 |
3 |
2 |
2 |
3 |
3 |
4 |
5 |
6 |
7 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
значения x необходимо будет исключить из решения нера- |
||||||||||||||
венства, так как неравенство строгое. |
|
|
|
|||||||||||
2) В левую часть неравенства входят множители (3 − 2x )2 и |
||||||||||||||
( x + 2)4 , которые всегда положительны при x ≠ |
3 |
и x ≠ −2 . |
||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
С учетом сказанного и из свойств неравенств получим неравенство, равносильное исходному:
(3x −1)(3x +1)( x − 2) x ( x + 3) > 0 |
(1) |
3)Отметим на координатной прямой значения x , при которых левая часть неравенства обращается в нуль
Это значения 1 ; − 1 ; 2; −3; 0 . Проведем через отложенные точки
33
волнообразную линию начиная справа сверху. Вся координатная прямая разбилась на 6 промежутков. Самый правый из них (2; +∞ ) положительный, далее знаки в промежутках чередуют-
ся. То есть на тех промежутках, где кривая проходит выше координатной прямой (знак "+") выполняется неравенство (1), заштрихуем эти промежутки.
4) Теперь можно на координатную прямую нанести точки
98 |
В.А.Битнер |
|
|
p 2
p 3
|
|
x = 3 и |
x = −2 . Все нанесенные точки – так называемые |
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
"выколотые". Окончательное решение исходного неравен- |
||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
ства есть: (−3; −2) −2; − |
|
0; |
(2; +∞ ) . |
|||||
|
|
|
|
|
|
|
3 |
|
3 |
|
x3 − 27 |
≤ 0 |
|
|
|
|
|
||||
x3 |
+ 8 |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
Решение: |
|
|
|
|
|
|||||
Имеем: |
( x − 3)(x2 + 3x + 9) |
≤ 0 . Но (x2 + 3x + 9) > 0 и |
||||||||
( x + 2)(x2 − 2x + 4) |
||||||||||
|
|
|
|
|
|
|
|
|||
x2 − 2x + 4 > 0 при x R , так как D < 0 |
||||||||||
Поэтому исходное неравенство равносильно неравенству |
||||||||||
x |
− 3 |
|
|
( x − 3)( x + 2) ≤ 0 |
|
|
|
|||
|
≤ 0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
x + 2 |
|
|
x ≠ −2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Ответ: (−2; 3].
( x + 3)(5 − x ) > 0 ( x + 3)( x − 5) < 0 ( x + 3)( x − 5)(2 x − 5) < 0 |
|
2x − 5 |
2x − 5 |
;
Ответ: (−∞; −3) (2, 5; 5)
p 4 |
(2x − 9)( x −1) |
|
|
(2x − 9)( x −1) |
≤ 0 |
|
||
|
x2 |
|
|
|
|
|||
|
|
|
|
≤ 0 |
|
x + 4 |
|
|
|
( x + 4)5 |
(2x − 6)4 |
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
x = 0, x ≠ 3 |
|
|
|
( x − 4, 5)( x −1)( x + 4) ≤ 0
x = 0, x ≠ 3, x ≠ −4
Ответ: (−∞; −4) [1; 3) (3; 4, 5] {0}
p 5 x + 2 − x
> 0
4 − x2
Решение:
Краткий курс школьной математики |
|
|
|
|
|
|
|
|
|
|
99 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x = −2, x = 0 - нули модулей, нанесем их на числовую прямую с |
|||||||||||||||||||
|
учетом, что x ≠ −2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решим неравенство на каждом из получившихся трех проме- |
|||||||||||||||||||
|
жутков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x < −2 |
|
|
|
|
|
x < −2 |
|
|
|
|
x < −2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
− x − 2 + x |
|
−2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
> 0 |
|
|
|
|
|
|
> 0 |
|
|
( x + |
2)( x − 2) > |
0 |
|||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
4 − x |
|
|
|
|
|
4 |
− x |
|
|
|
|
|
|
|
|
|||
|
|
x < −2 |
|
|
x < −2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
. |
|
Получили x < −2 |
(1) |
|||||||||
|
|
x − 2 |
< 0 |
|
x < 2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
−2 < x ≤ 0 |
|
−2 |
< x ≤ 0 |
|
|
|
−2 |
< x ≤ 0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) x + 2 + x |
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|||||||
|
|
|
|
> 0 |
|
|
|
|
|
|
|
|
|
|
|
< 0 |
( x |
+ 1)( x − 2) < 0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
4 − x |
|
|
|
|
|
( x + 2)( x − |
2) |
|
|
|
|
|
||||||
|
|
−2 < x ≤ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
. |
Получили −1 < x ≤ 0 |
|
|
(2) |
|||||||||||
|
|
−1 < x |
< 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x > 0 |
|
|
|
|
x > 0 |
|
|
|
|
x > 0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3) x + 2 − x |
|
|
|
|
|
x2 |
|
|
( x + 2)( x − 2) < 0 |
|
|||||||||
|
|
2 |
> 0 |
|
|
4 − |
|
> 0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
4 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Получили 0 < x < 2 |
|
|
(3) |
||||||||||
|
|
−2 < x |
< 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Из (1), (2) и |
(3) |
получаем |
решение исходного |
неравенства: |
|||||||||||||||
|
x < −2; −1 < x < 2 . Ответ: (−∞; −2) (−1; 2) . |
|
|
|||||||||||||||||
Упражнения для самостоятельного решения. |
|
|
||||||||||||||||||
Решить неравенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p 1 |
3x2 − 7 x + 2 < 0 |
|
|
p 112 |
|
|
x2 + 6x |
≥ 0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 − 3x − x |
|
|
|
|||
p 2 |
x2 − x + 2 ≥ 0 |
|
|
|
|
|
p 12 |
|
|
|
( x −1)( x − 2)( x + 2)3 x2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x −1)( x +1)( x − 3)4 |
≥ 0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

100 |
В.А.Битнер |
|
|
p 3 |
5x − x2 ≥ 0 |
|
p 4 |
x2 < 16 |
|
p 5 |
x − 4 |
≤ 0 |
|
|
|
|
x − 2 |
|
p 6 |
− x2 − 5x + 6 ≥ 0 |
|
p 7 |
4x2 + 4x + 1 ≤ 0 |
||||
p 8 |
x + 2 |
> 2 |
|
||
|
|
||||
|
3 − x |
||||
p 9 |
2 |
+ 2 x −11 |
|
||
|
2x |
|
< 1 |
||
|
|
|
|
||
|
x |
2 + x +1 |
|||
p 10 |
x6 + 9x3 + 8 ≤ 0 |
||||
Ответы:
p 1 |
1 |
|
|
||
|
|
|
|
; 2 |
|
|
|
||||
|
3 |
|
|
||
p 2 |
R |
|
|
||
p 3 |
[0; 5] |
||||
p 4 |
(−4; 4) |
||||
p 5 |
(2; 4] |
||||
p 6 |
[−6;1] |
||||
p 7 |
|
1 |
|||
|
− |
|
|
||
|
|
||||
|
|
2 |
|||
p13
p14
p15
p16
p17
p18
p19
p202
p112
p12
p13
p14
p15
p16
p17
2x2 +16 x − 3
x2 + 8x
> 2
x2 + 5x − 6 < 0
x2 + 4 x < 0
x + 4 ≤ 0x − 2
x ( x − 5) < 0
|
6 − x |
≥ 0 |
|||
|
|||||
x |
+ 3 |
|
|
|
|
|
|
|
|
||
|
1 |
≤ − |
1 |
|
|
|
|
2 |
|
||
x |
|
|
|
||
x − 6 > x2 − 5x + 9
1≥ 1 x 3
|
|
x |
2 |
+ 5x |
< 6 |
||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x +1 |
≤ 1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x2 − 5x + 4 |
|
≤ 1 |
||||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − 4 |
|
||||
|
|
|
|
|
|
|
|||
[−6; −4) [0;1)
[−2; −1) [2; 3) (3; +∞ ) {0} (−8; 0)
(−4; 0) (0; 2) [2; 0) (1; 3)
