Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki

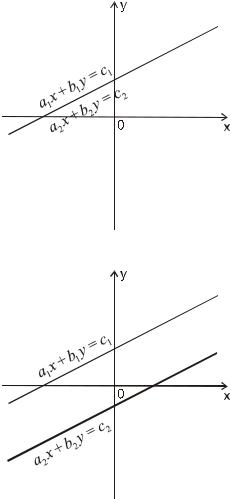
Краткий курс школьной математики

111

p 1

x − 3 y = 1

x = 1 + 3 y

x

= 1 + 3

y

x = 2

1

(1 + 3 y ) + 3 y = 13

1

2x + y =

4

6

21y = 7

y =

3

2

Ответ:

2;

1

.

2

p 2

При каком значении параметра a прямые, заданные

112

В.А.Битнер

уравнениями x + ay = 2 и 3x − 2 y = 6 совпадают?

Решение:

x + ay = 2

Имеем систему:

2

, откуда a = −

2

.

x −

y = 2

3

3

Ответ: при a = −

2

.

3

p 3 2x + 3 y = −1

10 x + 15 y = −5

+ 8 y

= 2

5x + 4 y = 1

10 x

−1 − 3 y

−1 + 3

7 y = −7

x =

=

= 1

2

2

x + y − z = 2

x + y − z = 2

− 3 y + 6z = −3

y − 2 z = 1

7 y

= 7

= 1

y

114

В.А.Битнер

p 8 x − 3 y + z = 7

x − 3 y + z = 7

x − 3 y + z = 7

3x + y − 2z = 3

10 y − 5z = −18

10 y − 5z = −18

10 y − 5z = − 7

0 = 11 - ложно,

x + 7 y − 4z = 0

o 7

a b

(a b ) и (c d ) - строки определителя,

a

и

b

- его столбцы. Обыч-

c

d

a

b

но определитель обозначают , то есть

=

.

c

d

То есть

= 0 тогда и только тогда, когда

a

=

b

.

c

d

p 1

1

2

p 22

2

3

2

3

= 5 + 6 = 11

= 0 , так как

=

.

−3 5

4

6

4

6

118

В.А.Битнер

a11

a12

a13

=

a21

a22

a23

- главный определитель системы (2),

a31

a32

a33

b1

a12

a13

a11

b1

a13

a11

a12

b1

x =

b2

a22

a23

, y =

a21

b2

a23

,

z =

a21

a22

b2

- вспомогатель-

b3

a32

a33

a31

b3

a33

a31

a32

b3

Правило 1

e главный определитель системы (2)

≠ 0 , то система имеет

единственное решение

x =

x

, y =

y

, z =

z

. То есть система

(1) имеет единственное решение, если

a1

≠

b1

.

a2

b2

Правило 2

e

= 0 , а

x ,

y или

z ≠ 0 , то система (2) не имеет решения.

Правило 3

e

= x =

y =

z = 0 , то система (2) имеет бесконечно много

решений.

6

2

−1

=

4

−1 3

= 6 (−1) (−2) + 2 3 3 + 4 2 (−1) − 3 (−1) (−1) −

3

2

−2

Краткий курс школьной математики

119

−4 2 (−2) − 2 3 6 = 12 + 18 − 8 − 3 + 16 − 36 = −1;

2

−1

2

x =

−3 −1 3

= 4 + 18 + 6 − 3 −12 −12 = 1 ;

3

2

−2

2

−1

6

y =

4 −3 3

= 36 + 18 −12 − 9 − 54 + 16 = −5 ;

3

3

−2

2

2

6

z =

4

−1 −3

= −18 −18 + 16 + 6 − 24 + 36 = −2 .

3

2

3

x =

x

=

1

= −1; y =

y

=

−5

= 5; z =

z

=

−2

= 2 .

−1

−1

−1

p 2 7 x − 8 y − 5z = 4

−9x + 6 y −11z = −1

+ 13z = 3

6x −11y

Решение:

−8

−5

7

=

−9 6 −11

= 7 6 13 + (−8) (−11) 6 + (−9) (−11) (−5) −

6

−11

13

4

−8

−5

x

=

−1

6

−11

= 312 + 264 − 55 + 90 −104 − 484 = 13 ;

3

−11

13

4

−5

7

y

=

−9

−1

−11

= −91 − 264 + 135 − 30 + 468 + 231 = 449 ;

6

3

13

120

В.А.Битнер

−8

4

7

z =

−9

6

−1

= 126 + 48 + 396 −144 − 77 − 216 = 133 ;

6

−11

3

x =

x

=

13

; y =

y

=

449

; z =

z

=

133

;

−1024

−1024

−1024

133

449

13

Ответ:

−

; −

; −

.

1024 1024

1024

p 1

2

x

y

p 22

x

y

+ 5

= 15

11

− 5

= 37

− 2 y = 3

− x = 25

x

4 y

p 3

2 x + y + z = 7

p 42

2x − 3 y + 4z = 5

x

+ 2 y + z = 8

−3x − 2 y + 5z = −6

+ y + 2z = 9

+ 4 y − 6z = −1

x

7 x

p 5

x + 2x

− x − 2x = −6

p 62

При каких значениях пара-

1

2

3

4

метра a система

− x2

+ 3x3

+ x4 = 4

3x1

(a + 1) x + 8 y = 4a

2 x1 + x2 − 2 x3

= 2

имеет

ax + (a + 3) y = 3a −1

2 x2 − x3 + 3x4 = 3

бесконечно много решений?

p 7

При

каких

значениях

параметра

a

прямые x + ay = 1 и

x − 3ay = 2a + 3 параллельны?

Указание: решить упражнение 2 способами (1 сп. – применить

условие параллельности прямых, предварительно записав

уравнения прямых в виде y = k1 x + b1

и

y = k2 x + b2 ; 2 сп. – за-

писать уравнения в виде системы и применить одно из правил

Крамера).

Ответы:

p 1

{(5;1)}

p 22

{(7;8)}