
Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki
.pdf
Краткий курс школьной математики |
61 |
|
|
тогда из (1) получим:
y +1 = −3( x −1) или y = −3x + 2 - уравнение искомой прямой,
параллельной данной прямой.
b) Из условия перпендикулярности двух прямых имеем
k |
= −3, k |
|
= − |
1 |
= |
1 |
, тогда из (1) получим |
||||||
2 |
|
|
|||||||||||
1 |
|
|
|
|
k1 |
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
y + 1 = |
1 |
( x −1) или y = |
1 |
x − |
4 |
- уравнение искомой прямой, |
|||||||
|
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
3 |
3 |
|
|||
перпендикулярной данной прямой. Ответ:
a)y = −3x + 2 ;
b)y = 1 x − 4 .
33
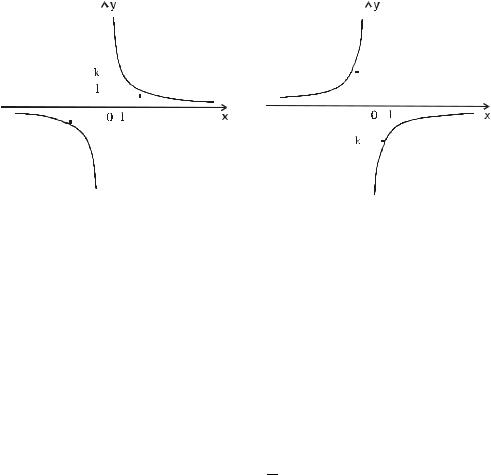
(2)Обратная пропорциональность.
o 2 Функция вида y = k , где k R , кроме k = 0 , называется об- x
ратнопропорциональной зависимостью или обратной пропорциональностью.
Исследуем функцию y = k в общем виде. x
1. D ( y ) = (−∞; 0) (0; +∞ ) ;
2. f (− x ) = |
k |
= − |
k |
= − f ( x ) , функция нечетная, график симметричен |
− x |
|
|||
|
|
x |
||
началу координат;
3.x ≠ 0, y ≠ 0 , то есть точек пересечения с осями координат нет.
4.Знаки функции:
a)e k > 0 , то y < 0 , e x < 0 и y > 0, e x > 0 ;
b)e k < 0 , то y < 0 , e x > 0 и y > 0, e x < 0 ;
5.Возрастание, убывание функции:
a)e k > 0 ,
то функция убывает от 0 до −∞ , e x (−∞; 0) и
62 |
В.А.Битнер |
|
|
функция убывает от +∞ до 0 , e x (0; +∞) .
b) e k < 0 ,
то функция возрастает от 0 до +∞ , e x (−∞; 0) и
функция возрастает от −∞ до 0 , e x (0; +∞) .
6.Экстремумов функция не имеет.
7.E ( y ) = (−∞; 0) (0; +∞) ;
8.График.
а) k > 0 |
|
|
|
|
|
|
|
б) k < 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
График обратной пропорциональности называется гиперболой.
Решение упражнений.
Построить графики функций
p 1 |
y = |
2 |
+ 1 . |
|
|
||||
x − 3 |
||||
|
|
|
График легче всего строить переносом осей координат x0 = 3, y0 = 1 .
( x0 ; y0 ) или (3;1) - точки сдвига графика функции вдоль осей координат.
2
Построим график функции y1 = в системе координат x1 01 y1 . x
Затем перенесем ось 01 y1 на "-3", а ось 01 x1 на "-1", тем самым

Краткий курс школьной математики |
63 |
|
|
получим искомый график в новой системе координат x0 y .
p 2 |
y = |
x −1 |
. |
|
|
|
|
|
|
|
|||||
|
|
x + 1 |
|
|
|||
|
Преобразуем выражение к виду y = |
x + 1 − 2 |
= − |
2 |
+ 1 и по- |
||
|
|
|
|||||
x + 1
строим график данной функции так же, как в p 1. x0 = −1; y0 = 1
(3)Степенная функция
1) с натуральным показателем;
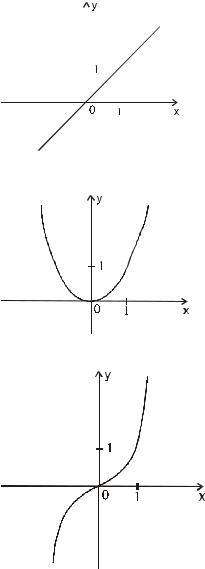
o 3 Функция вида y = xn , где n N , называется степенной функцией с натуральным показателем.
64 |
|
|
|
|
В.А.Битнер |
|
|
|
|
|
|
r эту функцию при n = 1, 2, 3, 4,..., 2k − 1, 2k , где k N . |
|
||||
1 n = 1, y = x |
|
|
Функция |
нечетная, |
|
. |
|
|
|
график |
симметри- |
|
|
|
|||
|
|
|
|
чен началу коорди- |
|
|
|
|
|
нат, |
|
|
|
|
|
D ( y ) = R, E ( y ) = R |
|
|
|
|
|
||
|
|
|
|
O (0; 0) - точка пе- |
|
|
|
|
|
||
|
|
|
|
ресечения графика |
|
|
|
|
|
с осями. |
|
|
|
|
|
|
|
2n = 2, y = x2
.График называется параболой
3n = 3, y = x3
.График называется кубической параболой
4n = 4, y = x4
.График называется
Функция четная, график симметричен оси 0 y ,
D ( y ) = R, E ( y ) =
= [0; +∞ )
O (0; 0) - точка пе-
ресечения графика с осями.
Функция нечетная, график симметричен началу координат,
D ( y ) = R, E ( y ) = R
O (0; 0) - точка пе-
ресечения графика с осями.
Свойства и график схожи со свойствами и графиком функции y = x2 .

Краткий курс школьной математики |
65 |
|
|
биквадратной
параболой
5 |
n = 2k −1, y = x2 k −1 |
. |
|
6 |
n = 2k , y = x2 k |
. |
|
- степенная функция с нечетным натуральным показателем. Свойство и график схожи со свойствами и графиком функции (при всех k N , k ≥ 2 )
- степенная функция с нечетным натуральным показателем. Свойства и график схожи со свойствами функций y = x2 и y = x4 .
2) с целым показателем;
o 4 |
Функция вида y = x p , где p Z , называется степенной функ- |
|
цией с целым показателем. |
При |
p = 0 y = x0 = 1 , обычно эту функцию не рассматривают, так как |
она не характерна для степенной функции. При p = 1, 2, 3,…имеем степенную функцию с натуральным показателем, которая рассмотрена ранее. Поэтому рассмотрим степенную функцию с отрицательным це-
лым |
показателем, то есть рассмотрим |
эту функцию при |
|||
p = −1; −2; −3;…; −2k +1; −2k , k N . |
|
||||
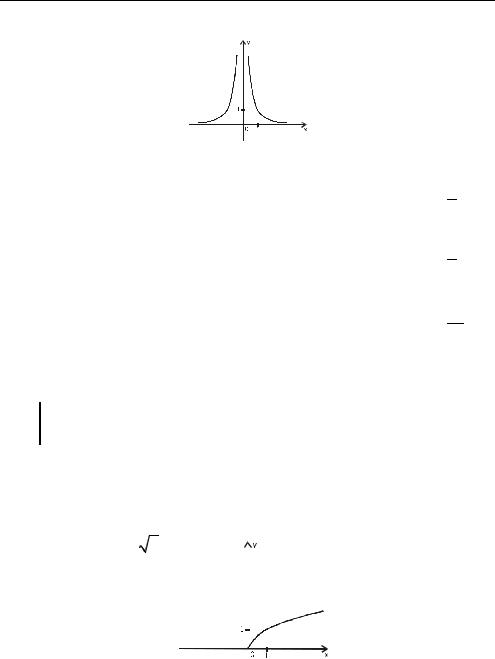
1. |
p = −1, y = x−1 = |
1 |
|
Функция нечетная, |
|
x |
график симметричен |
||||
|
|
||||
|
|
|
|
началу координат, |
|
D ( y ) = (−∞; 0) (0; +∞ )
E ( y ) = (−∞; 0) (0; +∞)
66 В.А.Битнер
2. |
p = −2, y = x−2 = |
1 |
Функция четная, гра- |
x |
фик симметричен оси |
||
|
2 |
|
|
|
|
|
ординат, |
D ( y ) = (−∞; 0) (0; +∞ )
E ( y ) = (0; +∞ ) .
3. |
p = −3, y = x−3 = |
1 |
3 |
x
4.p = −2k +1,
|
y = x |
−2 k +1 |
= |
1 |
|
|||
|
|
|
|
|
||||
|
|
|
2 k |
−1 |
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
x |
|
|
5. |
p = −2k , |
|
|
|
|
|
|
|
|
y = x |
−2 k = |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 k |
|
|||
|
|
|
|
|
|
|
||
x
Свойства и график этой функции схожи со
свойствами и графиком функции y = 1 . x
Свойства и график этой функции схожи со
свойствами и графиком функции y = 1 . x
Свойства и график этой функции схожи со
свойствами и графиком функции y = 12 . x
3) с рациональным показателем.
o 5 Функция вида y = xr , где r Q , называется степенной функцией с рациональным показателем.
r эту функцию при r = |
1 |
; |
1 |
;…; |
1 |
; |
1 |
|
, где n N . |
||||||
|
|
|
2n + 1 |
||||||||||||
|
|
2 3 |
|
2n |
|
||||||||||
1. |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Функция ни четная, |
r = |
, y = x 2 = x |
|
|
|
|
ни нечетная, |
|||||||||
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
D ( y ) = [0; +∞) , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E ( y ) = [0; +∞ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0; 0) - точка пересе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чения с осями коор- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
динат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Краткий курс школьной математики |
67 |
|
|
2. |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Функция |
нечетная, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
r = |
|
, y = x |
3 = 3 x |
|
график симметричен |
|||||||||||||||
|
3 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
началу |
координат, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D ( y ) = R , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E ( y ) = R , |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0; 0) - точка пересе- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чения с осями коор- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
динат. |
|
|||
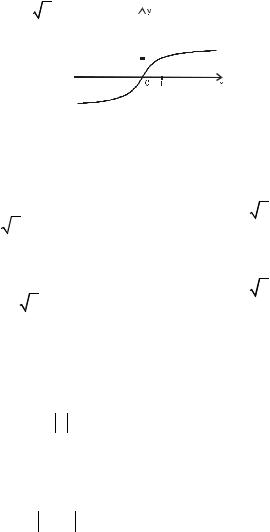
3. |
r = |
1 |
, |
|
|
|
|
|
|
|
|
|
- корень четной степени из x . Свойства и |
||||||||
|
|
|
|
|
|
|
|
|
|
график этой функции схожи со свойствами |
|||||||||||
|
|
2n |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
и графиком функции y = |
|
x . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y = x 2 n = 2 n x |
|
|
|
|
|
|
||||||||||||||
4. |
r = |
1 |
|
, |
|
|
|
|
|
|
|
- корень нечетной степени из x . Свойства и |
|||||||||
|
|
|
|
|
|
|
|
|
|
график этой функции схожи со свойствами |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2n +1 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
и графиком функции y = |
3 |
x . |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y= x 2 n +1 = 2 n +1 x
(4)Функции с модулем.
1.r функцию y = f ( x ) , она четная, значит, график ее симметричен оси 0 y . Поэтому, чтобы построить график этой функции, надо по-
строить график функции y = f ( x ) при x > 0 и отразить его сим-
метрично оси 0 y , получим искомый график - см. рис.5.
2.r функцию y = f ( x ) , она неотрицательная, значит, график этой
функции весь лежит выше оси 0x (быть может, еще и касается ее). Чтобы построить график этой функции, надо построить график функции y1 = f ( x ) и часть графика, расположенную ниже оси 0x ,
отразить симметрично оси 0x - см. рис.6.
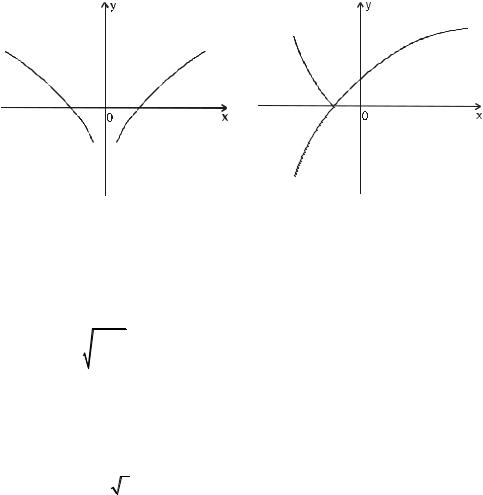
68 |
В.А.Битнер |
|
|
рис.1 |
рис.2 |
(5)Построение различных графиков функций.
Построить графики функций
p1 |
y |
= 2 |
x − |
1 |
−1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Строим |
график |
этой функции переносом |
осей |
координат, |
||||||||||||||
|
x |
= |
1 |
; y |
= −1 , |
где точка ( x ; y |
|
) - точка сдвига графика функ- |
|||||||||||
|
|
0 |
|||||||||||||||||
|
0 |
2 |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ции вдоль осей координат. |
|
|
|
|
|
|
||||||||||||
|
1. |
В |
системе |
координат |
x1 01 y1 строим |
график |
функции |
||||||||||||
|
|
y1 = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x . |
|
|
|
|
|
|
|
|
|
|
|||||
|
Переносим ось |
0 y на " − |
1 |
|
", ось 0 x - на "+1", получим иско- |
||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мый график в системе координат x0 y .

Краткий курс школьной математики |
69 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
3 |
|
|
|
|
|
|
|
||
p2 |
y = |
|
|
|
x + |
|
+ 1 . |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
При построении графика используем тот же способ переноса |
|||||||||||||||
|
осей координат. |
|
|
|
|
|
|
|
||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
− |
|
|
|
;1 - |
точка сдвига. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1. |
|
Строим |
график функции |
y |
= |
1 |
x3 в системе координат |
||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x1 01 y1 . |
|
|
|
|
|
|
|
|
|
||||
|
Переносим ось 0 y на " |
3 |
", ось 0 x - на "-1", получим искомый |
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
график.
70 |
В.А.Битнер |
|
|
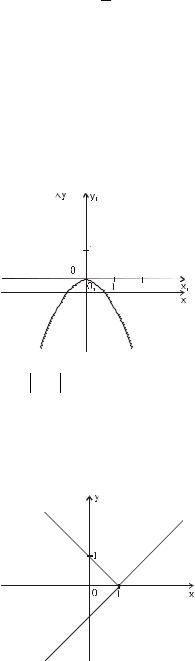
p3
p4
y = − ( x −1)2 + 1 .
|
|
2 |
|
|
|
1 |
|
|
|
1; |
|
- точка сдвига, в данном случае параболы эта точка явля- |
||
|
||||
|
2 |
|
|
|
ется еще и вершиной параболы. |
|
|
||
1. |
Строим график функции |
y = −x2 |
в системе координат |
|
|
|
|
1 |
|
|
x1 01 y1 . |
|
|
|
Переносим ось 0 y на "-1", ось 0 x - на " − |
1 |
". Получим иско- |
|||
|
|||||
1 |
1 |
1 |
1 |
2 |
|
|
|
|
|
|
|
мый график.
y = x −1 .
При построении графика см. (4)-2.
1.Строим график функции y1 = x −1.
2.Часть этого графика, расположенного ниже оси 0x , отобразим симметрично оси 0x , получим искомый график.
