
Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki
.pdf
Краткий курс школьной математики |
141 |
|
|
Ответы:
p 1 1
3
p 3 3 ; 1 . 16 4
Указание.
n x, xq, xq2 , xq3 ,... -
бесконечная геометрическая прогрессия, у которой q < 1 , то-
гда
x2 , x2 q2 , x2 q4 , x2 q6 , ... -
тоже бесконечная геометрическая прогрессия со знаменате-
p 22 |
а) 3 |
53 |
; б) |
17 |
; в) −28 |
991 |
. |
||||
|
|
|
|
||||||||
|
|
|
90 |
|
99 |
9900 |
|
||||
p 42 |
1 |
|
|
7 |
|
|
|
|
|||
|
|
|
; − |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
2 |
|
|
9 |
|
|
|
|
|||
лем q 2 < 1 .
(10) Решения смешанных задач по прогрессии.
p 1 Между числом 3 и неизвестным числом вставлено еще одно число так, что все три числа образуют возрастающую арифметическую прогрессию. Если средний член этой прогрессии уменьшить на 6, то получится геометрическая прогрессия.
Найти неизвестные число. Решение:
1. Из условия и определения арифметической прогрессии имеем: 3; 3 + d ; 3 + 2d , где 3 + 2d - неизвестное d > 0 .
2.Из условия же: g 3; 3 + d − 6; 3 + 2d . Из характеристического свойства геометрической прогрессии
(d − 3)2 = 3(3 + 2d ), d 2 −12d = 0, d = 0 - не удовлетворяет ус-
ловию, d = 12 .
Тогда неизвестное число 3 + 2d = 3 + 24 = 27 . Ответ: 27.
p 2 Сумма трех чисел , составляющих арифметическую прогрессию равна 15. Если к этим числам прибавить соответственно 1, 1 и 9, то получатся три числа, составляющих геометрическую
142 |
В.А.Битнер |
|
|
прогрессию.
Найти исходные три числа. Решение:
1. n x, x + d , x + 2d - искомые числа, тогда x + 1, x + d + 1 и x + 2d + 9 составляют геометрическую прогрессию.
2.Из условия и по характеристическому свойству геометрической прогрессии имеем: x + x + d + x + 2d = 15 .
(x + d + 1)2 = ( x + 1)( x + 2d + 9) , откуда
x + d = 5, ( x + 1) (5 + d + 9) = 36, ( x + 1) (d + 14) = 36 , но
d = 5 − x , подставим:
( x + 1) (5 − x + 14) = 36, ( x + 1) (19 − x ) = 36, x2 −18x + 17 = 0,
.
x1 = 1, x2 = 17
а) x = 1, d = 5 −1 = 4 и исходные три числа: 1, 5, 9;
б) x = 17, d = 5 −17 = −12 и исходные три числа: 17, 5, -7
Ответ: 1, 5, 9 или 17, 5, -7.
p 3 Найти четыре числа, из которых первые три составляют геометрическую прогрессию, а последние три – арифметическую прогрессию, причем сумма крайних чисел равна 32, а сумма средних чисел равна 24.
Решение:
1.n x, xq, xq2 , y - искомые числа, тогда ÷xq, xq2 , y , и по характеристическому свойству арифметической прогрессии xq + y = 2xq2 .
2.Из условия и из полученного получили систему:
x + y = 32 |
xq − x = 2xq2 |
− 32 |
|
|
|
|
|
xq + xq 2 |
= 24 |
xq + xq2 = 24 |
|
|
2 |
|
|
xq + y = 2xq |
y = 32 − x |
|
|
|
|
|
|
|
xq |
2 |
|
xq |
|
x |
|
x |
(2q2 − q + 1) = 32 |
|||||
|
|
|
|
2 |
|
|
− |
|
+ |
|
= 32 |
|
|
|
|
|
|
|
3. Решим систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
xq2 |
+ xq = 24 |
|
|
x |
( |
q 2 |
+ |
q |
) = 24 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разделим 1 уравнение системы на второе, получим: |
||||||||||||||||||
|
2q2 − q + 1 |
= |
4 |
6q2 − 3q + 3 = 4q2 + 4q . |
|
|
|
|
||||||||||
|
q 2 + q |
|
|
|
|
|
||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Краткий курс школьной математики |
143 |
|
|
|
2q2 − 7q + 3 = 0, D = 49 − 24 = 25, q = |
7 − 5 |
= |
1 |
, q |
= |
7 + 5 |
= 3 . |
|
|||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
4 |
|
2 |
|
2 |
|
4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) |
q = |
1 |
, |
тогда |
x = |
|
|
24 |
|
|
= 32, y = 32 − 32 = 0 |
и 32, |
16, |
8, 0 |
– |
|||||||
|
1 |
|
1 |
|||||||||||||||||||
|
2 |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
искомые числа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) |
q = 3 , |
тогда |
x = |
|
|
24 |
|
|
= 2, y = 32 − 2 = 30 |
и 2, |
|
6, |
18, |
30 |
– |
|||||||
|
|
|
|
|
|
|||||||||||||||||
9 + 3 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
искомые числа.
Ответ: 32, 16, 8, 0 или 2, 6, 18, 30.
Упражнения для самостоятельного решения.
p 1 |
3 числа составляют геометрическую прогрессию. Если от |
||||||||||||||||
|
третьего отнять 4, то числа составят арифметическую прогрес- |
||||||||||||||||
|
сию. Если же от второго и третьего членов этой арифметиче- |
||||||||||||||||
|
ской прогрессии отнять по 1, то снова получится геометриче- |
||||||||||||||||
|
ская прогрессия. Найти эти числа. |
|
|
||||||||||||||
p 2 |
Найти четыре числа, первые три из которых составляют гео- |
||||||||||||||||
|
метрическую прогрессию, а последние три – арифметическую |
||||||||||||||||
|
прогрессию. Сумма крайних чисел равна 21, а сумма средних |
||||||||||||||||
|
равна 18. |
|
|
|
|
|
|
|
|
|
|
||||||
p 3 |
Три числа, из которых третье равно 12, образуют геометриче- |
||||||||||||||||
|
скую прогрессию. Если вместо 12 взять 9, то три числа составят |
||||||||||||||||
|
арифметическую прогрессию. |
|
|
|
|
|
|||||||||||
|
Найти эти числа. |
|
|
|
|
|
|
|
|
|
|||||||
Ответы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p 1 |
1; 3; 9 или |
p 2 |
3; 6;12;18 или |
|
p 3 3; 6;12 или |
||||||||||||
|
|
1 |
; |
7 |
; |
49 |
|
|
18 |
3 |
;11 |
1 |
; 6 |
3 |
; 2 |
1 |
27;18;12 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
9 |
|
9 |
9 |
|
|
4 |
4 |
4 |
|
2 |
|
|||||

144 |
В.А.Битнер |
|
|
Тема XX. Тригонометрия.
(1)Единичная числовая окружность. Радианное измере- ние угловых величин. Формулы длины окружности и площади кругового сектора. Определение тригоно- метрических функций.
o 1 Окружность радиуса 1 с центром в начале координат называется единичной числовой окружностью. Ее уравнение имеет вид x2 + y 2 = 1 - см. рис.1.
А круг единичного радиуса с центром в начале координат называется тригонометрическим кругом.
рис.1 |
180 |
1 радиан равен |
π |
пишут 1 рад. |
рис.2 |
(1)
l = α r |
- длина дуги в α радиан окружности радиуса r . |
(2) |
||||
S = |
α r |
2 |
= |
l r |
- площадь сектора круга радиуса r , |
(3) |
|
|
|
||||
|
|
|
||||
22
дуга которого содержит α радиан.
Из формулы (1) следует, что π рад. = 180 |
(4) |
-это основная формула при переводе радианной меры углов в градусную и наоборот.
Обозначение рад. обычно не пишут.

Краткий курс школьной математики |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
145 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
p 1 |
|
Из (4) следует, что 90 |
= |
π |
; 30 = |
π |
; |
45 |
= |
π |
; 60 = |
π |
; |
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
6 |
|
|
|
|
4 |
|
|
|
|
3 |
|
|
|
|||
|
|
360 = 2π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p 2 |
|
Из формулы (4) также следует, что |
3π |
= 270 ; |
2π |
= 120 ; |
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
||||
|
|
|
5π |
= 150 ; |
− |
π |
= −30 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
o 2 |
|
n P (1; 0) и P |
( x ; y ) , где P = Rα (P ) - см. рис.2. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
0 |
|
α |
α |
α |
|
|
|
α |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Тогда yα = sin α - синус, xα |
= cosα - косинус числа α . |
|
|
|||||||||||||||||||||||
Дадим словесное определение синуса и косинуса числа α . |
|
|
||||||||||||||||||||||||||
o 2' |
|
Синусом числа α |
называется ордината |
y |
точки |
|
P |
( x ; y ) , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
α |
|
α α |
||
|
|
полученной в результате поворота |
Rα |
точки P (1; 0) |
вокруг |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|||
|
|
начала координат O (0; 0) на α радиан. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Косинусом |
числа |
α |
называется |
абсцисса |
|
x0 |
этой |
точки |
||||||||||||||||||
P( x ; y ) .
αα α
o 3 |
|
tgα = |
yα |
|
= |
sin α |
, cos α ≠ 0 . |
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
xα |
|
|
cosα |
|
|
|||||
o 3' |
|
Тангенсом числа α называется отношение ординаты y |
точки |
|||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
P |
( x ; y |
) к абсциссе x |
этой же точки, при условии, что |
|||||||||
|
|
α |
α α |
|
|
|
|
|
α |
|
|
|||
|
|
xα ≠ 0 . То есть тангенсом |
α называется отношение |
sin α к |
||||||||||
|
|
cos α , когда cos α ≠ 0 . |
|
|
||||||||||
o 4 |
|
ctgα = |
xα |
|
= |
cos α |
, sin α ≠ 0 . |
|
|
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
yα |
|
|
|
sin α |
|
|
|||
Синус, косинус, тангенс и котангенс называются основными тригонометрическими функциями.
146 |
|
|
|
|
|
|
|
|
|
|
|
В.А.Битнер |
|
|
|
|
|
|
|
|
|
|
|
|
|
o 5 |
|
secα = |
1 |
|
= |
|
|
1 |
|
, cosα ≠ 0 . |
||
|
|
|
|
|
||||||||
|
|
|
cos α |
|||||||||
|
|
|
xα |
|
|
|||||||
o 5' |
|
Секансом числа α называется величина, обратная cos α ≠ 0 . |
||||||||||
|
||||||||||||
o 6 |
|
cosecα = |
1 |
|
= |
1 |
|
, sin α ≠ 0 . (косеканс числа α ) |
||||
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
yα |
|
|
sin α |
||||
1.D(sin) = R; E(sin) = [−1;1] .
2.D(cos) = R; E (cos) = [−1;1].
|
|
|
π |
|
π |
|
|
3. |
D(tg) = |
− |
|
+ π n; |
|
+ π n |
, n Z ; E (tg) = R . |
|
|
||||||
|
|
|
2 |
2 |
|
|
|
4. |
D(ctg) = (π n;π + π n ), n Z ; E (ctg) = R . |
|
||||||
|
|
|
π |
|
π |
|
, n Z ; E(sec) = (−∞; −1] [1; |
+∞) . |
5. |
D(sec) = |
− |
|
+ π n; |
|
+ π n |
||
|
|
|||||||
|
|
|
2 |
2 |
|
|
|
|
6. |
D(cosec) = (π n;π + π n), n Z ; E(cosec) = (−∞; −1] [1; +∞) . |
|||||||
(2)Основные тригонометрические тождества.
1.sin 2 α + cos2 α = 1 ;
2.tgα ctgα = 1;
3. |
1+tg2α = |
|
1 |
|
|
= sec2 α ; |
|
|
|
|
|
||||
cos2 |
|
|
|||||
|
|
α |
|||||
4. |
1+ctg2α = |
1 |
|
|
= cosec2 α . |
||
|
|
|
|
||||
|
2 |
|
|
||||
|
|
|
sin |
α |
|||
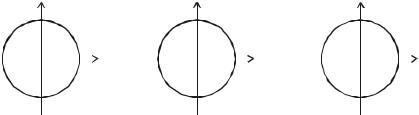
(3)Знаки тригонометрических функций по четвертям
y |
y |
y |
II |
I |
|
+ + |
|
|
- |
+ |
|
- + |
|
|
|
|
|
|
|
|
|
- 0 - |
|
x |
- |
0+ |
x |
+ 0 - |
x |
III |
IV |
|
|
|
|
|
|
sin |
|
|
|
cos |
|
tg, ctg |
|
Краткий курс школьной математики |
147 |
|
|
1.Синус положителен в верхней координатной полуплоскости и отрицателен в нижней.
2.Косинус положителен в правой координатной полуплоскости и отрицателен в левой.
3.Тангенс и котангенс положительны в I и III координатных четвертях и отрицательны во II и IV.
(4)Значения тригонометрических функций некоторых основных углов.
Углы |
|
π |
π |
π |
π |
|
3π |
|
2π |
|
π |
5π |
|
|
Триг. |
0 |
π |
2π |
− |
|
|||||||||
Функц. |
6 |
4 |
3 |
2 |
2 |
3 |
6 |
4 |
|
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
3 |
|
1 |
− |
2 |
sin |
2 |
0 |
−1 |
0 |
|
− |
2 |
|||||||
2 |
2 |
2 |
2 |
2 |
2 |
|
||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
3 |
2 |
1 |
|
−1 |
|
|
|
1 |
|
3 |
− |
2 |
cos |
1 |
0 |
0 |
1 |
− |
|
2 |
|||||||
2 |
2 |
2 |
|
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
||
|
tg |
|
|
0 |
1 |
3 |
− |
0 |
− |
0 |
− 3 |
3 |
1 |
|||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
− |
1 |
|
|
|
|
|
|||
|
ctg |
|
− |
3 1 |
0 |
− |
0 |
− |
3 |
− 3 |
1 |
|||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5)Четность тригонометрических функций.
o 7 |
|
Функции вида y = sin x, y = cos x, y = tg x, y = ctg x называются |
|
|
основными тригонометрическими функциями. |
t 1 |
|
Функция y = cos x - четная, а функции y = sin x , y = tg x и |
|
||
|
|
y = ctg x - нечетные. |
|
|
|

148 |
В.А.Битнер |
|
|
Так как для функции f ( x ) = cos x |
x R и выполняется условие |
f (− x ) = cos x = f ( x ) . |
|
А для функций f ( x ) = sin x, f ( x ) = tg x, f ( x ) = ctg x выполняются ус-
ловия f (− x ) = sin (− x ) = − sin x = − f ( x ) , tg (−x ) = −tg x, ctg (−x ) = −ctg x .
График функции y = cos x симметричен оси 0 y , а графики функций y = sin x , y = tg x, y = ctg x симметричны началу координат O (0; 0) .
(6)Периодичные функции. Периодичность тригономет- рических функций.
o 8 |
e |
для |
функции |
y = f ( x ) |
выполняется |
условие |
|
f ( x + T ) = f ( x − T ) = f ( x ) , где x, x + T , x − T D ( y ) |
и T R , |
||||
|
T ≠ 0 , то эта функция называется периодической с периодом |
|||||
|
T . |
|
|
|
|
|
Ясно, что eT - период функции y = f ( x ) , то kT - бесконечное мно-
жество периодов этой функции, где k Z .
o 9 Наименьший положительный период функции называется основным периодом этой функции.
t 2 Функции y = sin x и y = cos x периодичны с основным периодом T = 2π .
Так как sin ( x + 2π ) = sin ( x − 2π ) = sin x ,
cos ( x + 2π ) = cos ( x − 2π ) = cos x . Ясно, что 2π n , где n Z - множест-
во периодов этих функций.
t 3 Функции y = tg x и y = ctg x периодичны с основным периодом T = π .
Краткий курс школьной математики |
149 |
|
|
Так как tg ( x + π ) = tg ( x − π ) = tg x, ctg ( x + π ) = ctg ( x − π ) = ctg x . Ясно,
что π n , где n Z - множество периодов этих функций.
(7)Формулы приведения.
oФормулы тригонометрических функций углов
π ± α ,π ± α , 3π ± α , 2π − α называются формулами приведения
2 |
2 |
для тригонометрических функций.
Правила для применения формул приведения.
1.Перед приведенной функцией ставится знак, совпадающий со знаком приводимой функции, считая, что аргумент α находится в I четверти.
2.Функция не меняется, если в формуле приведения аргумент α вы-
yчитается или прибавляется к числам π или
|
π |
2π , то есть угол |
α прилегает к горизонталь- |
|
2 |
||
|
|
|
|
|
|
ному диаметру единичной числовой окруж- |
|
π |
|
0 (2π) ности (см. рис.1) |
|
0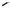 x 3. Функция меняется на кофункцию, если в
x 3. Функция меняется на кофункцию, если в
|
формуле приведения аргумент α вычитается |
|||||
3π |
или прибавляется к числам |
π |
или |
3π |
, то |
|
2 |
||||||
|
|
|||||
|
|
2 |
2 |
|
||
рис.1 |
есть угол α прилегает к |
вертикальному |
||||
|
диаметру (см. рис.1). |
|
|
|
|
|
zКофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.
p 1 |
sin (π − α ) = sin α |
|
||||
p 2 |
|
π |
|
|
|
|
|
cos |
|
|
− α |
= sin α |
|
|
|
|
||||
|
|
2 |
|
|
|
|
p 3 |
3π |
|
|
|
||
|
tg |
|
|
+ α |
= −ctg α |
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
p 4 |
cos (π + α ) = − cosα |
p 5 sin (π + α ) = − sin α |
||||
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В.А.Битнер |
p 6 |
tg (π − α ) = −tgα |
|
p 7 |
|
ctg |
|
3π |
− |
|
= tgα |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
α |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
(8) |
Графики тригонометрических функций. |
|
|
|
|||||||||||||
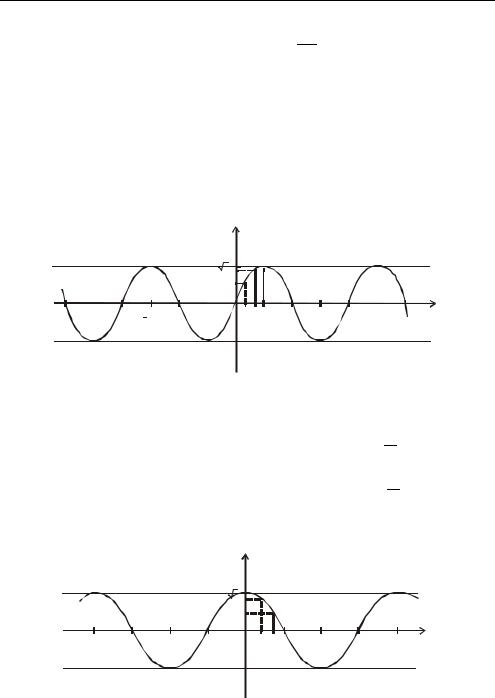
1. |
y = sin x |
- синусоида. |
При построении графика воспользовались |
||||||||||||||
|
формулой приведения sin (π − x ) = sin x , нечетностью (график сим- |
||||||||||||||||
|
метричен |
началу |
координат) |
|
и |
|
|
периодичностью |
функции |
||||||||
|
y = sin x (T = 2π ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-3π |
-2π 3π |
-π |
|
|
π π π |
|
π |
|
3π |
|
2π |
|
3π |
x |
||
|
|
2 |
|
|
|
6 |
3 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис.1 |
|
|
|
|
|
|
|
|
|
|
||
2. |
y = cos x - |
косинусоида или синусоида. График функции |
y = cos x |
||||||||||||||
|
можно построить, как график функции y = sin |
|
π |
, то есть пе- |
|||||||||||||
|
x + |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
реносом у графика функции |
y = sin x |
оси |
0 y |
на |
π |
- см.рис.1 и |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
рис.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
-2π − 3π |
-π |
− π |
|
|
5 π π |
|
|
π |
|
3π |
2π x |
|||||
|
|
2 |
|
2 |
|
|
6 |
3 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис.2 |
|
|
|
|
|
|
|
|
|
|
||
