
Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki
.pdf
Краткий курс школьной математики |
101 |
|||||
|
|
|
|
|
|
|
p 8 |
1 |
|
p 18 |
[3; 0) (0; 3] |
||
|
1 |
|
; 3 |
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
||
p 9 |
(−4; 3) |
p 19 |
(−2; 0] |
|||
p 10 |
(1; 2) |
|
p 202 |
[0;1, 6] [2, 5; +∞ ) |
||
Тема XVI. |
Иррациональные уравнения и |
|||||
|
|
|
|
|
неравенства. |
|
(1)Иррациональные уравнения.
o 1 Иррациональными называются уравнения, в которых неизвестные содержатся под знаком радикала.
При этом надо помнить, что в иррациональных уравнениях все радикалы понимаются в смысле их арифметических значений , то есть выражения под знаком радикала и сами радикалы должны быть неотрицательными.
При решении иррациональных уравнений стараются свести их к рациональным. При этом при возведении в четную степень могут появиться посторонние корни. Поэтому при решении иррациональных уравнений необходимо тщательно следить за областью допустимых значений переменных (о.д.з.) или в конце решения сделать проверку полученных корней.
Решение уравнений.
Решить уравнения. |
|
|
|
|||
p 1 |
|
|
|
|
|
|
|
x + 2 = x |
|
|
|
||
|
|
|
|
|
||
|
Решение: |
|
|
|
||
|
|
|
x + 2 ≥ 0 |
|
|
|
|
а) о.д.з. |
( x ≥ 0) |
б) Возведем в квадрат обе части |
|||
|
|
|
x ≥ 0 |
|
|
|
|
уравнения, |
получим: |
x + 2 = x2 x2 − x − 2 = 0, x = −1 - не |
|||
|
|
|
|
|
|
1 |
|
удовлетворяет о.д.з. x2 |
= 2 . |
Ответ: {2} . |
|||

102 |
В.А.Битнер |
|
|
p2
p3
p4
p5
p 6
p 7
|
x − 3 + |
|
2 − x = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x − 3 ≥ 0 |
|
|
x ≥ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
О.д.з. |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 − x ≥ 0 |
x |
≤ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ответ: . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 x − 3 + |
|
x = −2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ответ: , так как |
|
|
2 x − 3 + |
|
|
x > 0 , а "− 2 " < 0 . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x −1 − |
|
x − 3 = 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ответ: , так как при о.д.з. x ≥ 3 x −1 − |
x − 3 < 0 , а 3 > 0 . |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
( x − 5) ( x + 2 ) x − 7 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а) о.д.з. x ≥ 7 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x − 5 = 0 |
x = 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
+ 2 |
= |
0 |
|
= −2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
б) x |
x |
|
|
|
- не удовлетворяют о.д.з. |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
x |
− 7 |
= |
0 |
|
|
|
x |
= 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ответ: {7} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x + 2 − |
|
|
|
x − 6 = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Перепишем уравнение в виде |
x + 2 − 2 = |
|
x − 6 , |
|||||||||||||||||||||||||||||||
|
|
|
|
|
x + 2 ≥ 0 |
|
|
|
|
|
x ≥ −2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ≥ 6 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
а) о.д.з. |
|
x + 2 − 2 ≥ 0 |
|
x + |
2 ≥ 2 |
|
|
|
( x ≥ 6) . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 2 ≥ 4 |
|||||||
|
|
|
|
|
x − 6 ≥ 0 |
|
|
|
|
|
x ≥ 6 |
|
|
|
|
|
|
|
|
|
||||||||||||||
б) Возведем в квадрат обе части получившегося уравнения,
получим: x + 2 − 4
 x + 2 + 4 = x − 6
x + 2 + 4 = x − 6 
 x + 2 = 3, x + 2 = 9, x = 7 .
x + 2 = 3, x + 2 = 9, x = 7 .
Ответ: {7} .

 3x2 +1 +
3x2 +1 + 
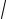 x2 + 3 =
x2 + 3 = 
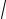 6 x2 +10
6 x2 +10
Решение:
а) о.д.з. x R ;
б) Возведем в квадрат обе части уравнения, получим: 3x2 + 1 + 2
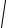 (3x2 + 1)( x2 + 3) + x2 + 3 = 6 x2 + 10 ,
(3x2 + 1)( x2 + 3) + x2 + 3 = 6 x2 + 10 ,

Краткий курс школьной математики |
103 |
|
|
p 8
p 9
p 10
2
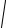 (3x2 + 1)( x2 + 3) = 2 x2 + 6,
(3x2 + 1)( x2 + 3) = 2 x2 + 6, 
 (3x2 +1)( x2 + 3) = x2 + 3 .
(3x2 +1)( x2 + 3) = x2 + 3 .
Разделим обе части уравнения на 
 x2 + 3 ≠ 0 , получим
x2 + 3 ≠ 0 , получим
3x2 +1 = x2 + 3, 3x2 + 1 = x2 + 3, x |
2 = 1, x = ±1. |
||
|
|
|
1,2 |
Ответ: {±1} . |
|
||
|
|
|
|
( x + 4)( x + 1) − 3 x2 + 5x + 2 = 6 |
|
||
Решение: |
|
||
Имеем: x2 + 5x + 4 − 3 |
x2 + 5x + 2 − 6 = 0 , |
||||||||
|
|
|
|
|
|
|
|
||
x |
2 + 5x + 2 − 3 x2 + 5x + 2 − 4 = 0 , введем замену |
||||||||
|
|
|
|
|
|
||||
|
|
x2 + 5x + 2 = y , где y > 0 , получили: y2 − 3x − 4 = 0, y = −1 - не |
|||||||
|
|
|
|
|
|
|
|
1 |
|
удовлетворяет о.д.з. для y , |
|||||||||
|
|
|
|
|
|
||||
y |
2 |
= 4 x2 + 5x + 2 = 4 x2 + 5x + 2 = 16 , |
|||||||
|
|
|
|
|
|
|
|
||
x |
2 + 5x −14 = 0, x = −7, x = 2 . |
||||||||
|
|
|
1 |
|
2 |
|
|||
Ответ: {−7; 2} .
3 x + 34 − 3
x + 34 − 3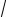 x − 3 = 1
x − 3 = 1
Решение:
Перепишем уравнение в виде: 3 x + 34 = 1 + 3
x + 34 = 1 + 3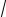 x − 3 , возведем в куб обе части уравнения, получим
x − 3 , возведем в куб обе части уравнения, получим
x + 34 = 1 + 3 3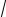 x − 3 + 3 3
x − 3 + 3 3 ( x − 3)2 + x − 3 , 3
( x − 3)2 + x − 3 , 3 x − 3 + 3
x − 3 + 3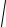 ( x − 3)2 −12 = 0 .
( x − 3)2 −12 = 0 .
Введем замену 3 x − 3 = y , получим y2 + y −12 = 0, y1 = 3, y2 = −4 ,
x − 3 = y , получим y2 + y −12 = 0, y1 = 3, y2 = −4 ,
а) y = 3 3 x − 3 = 3 x − 3 = 27, x1 = 30 ;
x − 3 = 3 x − 3 = 27, x1 = 30 ;
б) y = −4 3 x − 3 = −4 x − 3 = −64, x2 = −61 . Ответ: {−61; 30} .
x − 3 = −4 x − 3 = −64, x2 = −61 . Ответ: {−61; 30} .
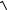 1 − x
1 − x
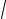 x2 −1 = x −1
x2 −1 = x −1
Решение: а) о.д.з. x ≥ 1
б) Возведем обе части уравнения в квадрат
1 − x
 x2 −1 = x2 − 2 x +1 −x
x2 −1 = x2 − 2 x +1 −x
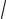 x2 −1 = x ( x − 2 ) , но x = 0 -
x2 −1 = x ( x − 2 ) , но x = 0 -

104 В.А.Битнер
не удовлетворяет о.д.з., поэтому сократим обе части уравнения на − x ≠ 0 , получим:

 x2 −1 = 2 − x , где x ≤ 2 , итак, о.д.з. 1 ≤ x ≤ 2 .
x2 −1 = 2 − x , где x ≤ 2 , итак, о.д.з. 1 ≤ x ≤ 2 .
2 2 5 5
x −1 = 4 − 4 x + x , x = . Ответ: . 4 4
Упражнения для самостоятельного решения.
Решить уравнения.
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 + 2 x |
− 7 = x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
p 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|||
|
|
9 − 5x = 3 − x + |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
3 − x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 − x − x |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
= |
|
|
6 − x − x |
|
||||||||||||||||||||
|
|
|
2 x − 5 |
|
|
|
|
|
|
|
|
x − 2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
p 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− 4 x |
+ 4 + |
|
|
|
|
2 |
− 6 x + 9 = 1 |
|||||||||||||||||||
|
|
|
x |
|
|
|
x |
||||||||||||||||||||||
p 9 |
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
x |
− 2 + |
|
x − 3 |
= |
|
2 x − 5 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
p 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11x + 3 |
− 2 − x = 9 x + 7 − |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
− |
|
x − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p 1 |
{28} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p 3 |
{−3} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p 5 |
{−3} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p22
p42
p62
p82
p102
p122
p22
p42
p62

 x − 5 +
x − 5 +  10 − x = 3
10 − x = 3

 2 x +1 = 2
2 x +1 = 2
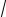 x −
x − 
 x − 3
x − 3
|
10 + x |
|
10 − x |
|
|
|
|
+ |
= 6 |
||||
|
|
|||||
|
x |
x |
||||
( x +1)
 x2 − 5x + 5 = x + 1
x2 − 5x + 5 = x + 1
( x + 3) ( x + 2) −
−4
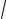 x2 + 5x + 2 = 4
x2 + 5x + 2 = 4

 x + 3
x + 3 x = 3
x = 3 
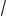 x − 3
x − 3 x
x
{6; 9}
{4}
{6} . Указание: записать уравнение в виде
|
10 |
|
|
|
10 |
|
|
|
|||
|
+ 1 + |
|
−1 = 6 и |
||||||||
|
|
|
|||||||||
|
x |
|
|
|
x |
||||||
ввести, например, за- |
|||||||||||
|
|
|
|
|
|||||||
мену |
|
10 |
−1 = y . |
||||||||
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
Краткий курс школьной математики |
|
|
|
|
|
105 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 7 |
[2; 3] . Указание: имеем |
p 82 |
{−1;1; 4} |
|
|
|
||||||||||
|
|
x − 2 |
|
+ |
|
x − 3 |
|
= 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p 9 |
{2; 3; 2, 5} |
|
|
|
|
|
|
p 102 |
|
|
−5 ± |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|||
|
|
|
|
|
|
|
|
|
|
2; 7; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 11 |
{2} |
|
|
|
|
|
|
|
p 122 |
{64} . Указание: сокра- |
||||||
|
|
|
|
|
|
|
|
|
|
тить числитель и зна- |
||||||
|
|
|
|
|
|
|
|
|
|
менатель дроби на |
||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ≠ 0 . |
|
|
|
|||
(2)Иррациональные неравенства.
o 2 Иррациональными называются неравенства, в которых неизвестные величины находятся под знаком радикала (корня).
При решении таких неравенств их чаще всего стараются свести к рациональным неравенствам, при этом используются основные свойства числовых неравенств, основные теоремы о действиях с неравенствами и следствия из них. При этом необходимо следить за тем, чтобы при преобразованиях неравенств каждый раз получалось неравенство, равносильное исходному. Тем более, что проверка полученных решений подстановкой затруднена.
При решении иррациональных неравенств следует помнить, что при возведении обеих частей неравенства в нечетную степень всегда получается неравенство, равносильное исходному. Если же обе части неравенства возводятся в четную степень, то полученное неравенство будет равносильно исходному и иметь тот же смысл лишь в том случае, если обе части неравенства неотрицательны.
Решение упражнений.
Решить неравенства:
p 1 |
x − 5 |
< 1 |
|
Решение:
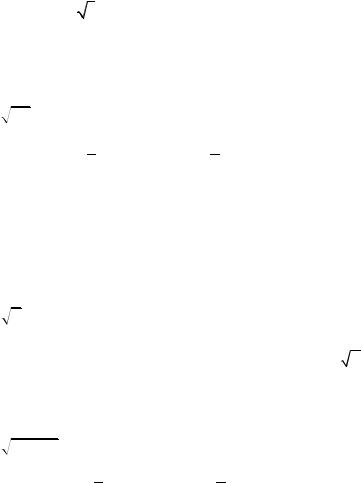
106 |
В.А.Битнер |
|
|
p 2
p 3
p 4
Так как D ( |
|
) = [0; +∞ ) и из свойств неравенств, имеем |
|
||
x − 5 ≥ 0 |
x ≥ 5 |
|
x − 5 < 1 |
x < 6 (5 ≤ x < 6) . |
|
Ответ: [5; 6) .

 − x ( x + 1) > 0
− x ( x + 1) > 0
Решение:
Так как D (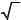 ) = [0; +∞ ) и E (
) = [0; +∞ ) и E (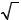 ) = [0; +∞ ) , то
) = [0; +∞ ) , то
− x > 0
x + 1 > 0, так как x = 0 не является решением исходного неравенства.
x < 0
x > −1 (−1 < x < 0) .
Ответ: (−1; 0) .

 x > −2
x > −2
Решение:
Неотрицательная левая часть (по определению 
 a ) при всех допустимых значениях x больше отрицательной правой части. Следовательно, x ≥ 0 .
a ) при всех допустимых значениях x больше отрицательной правой части. Следовательно, x ≥ 0 .
Ответ: [0; +∞ ) .

 9 x − 20 < x
9 x − 20 < x
Решение:
Так как D (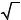 ) = [0; +∞ ) , E (
) = [0; +∞ ) , E (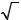 ) = [0; +∞ ) и из свойств нера-
) = [0; +∞ ) и из свойств нера-
|
|
|
|
|
9 x − 20 |
≥ 0 |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
x |
≥ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
венств имеем x > 0 |
|
|
|
|
9 |
|
|
|||||||
|
|
|
|
|
|
< x |
2 |
|
|
2 |
− 9 x + 20 |
> 0 |
||
|
|
|
|
|
9 x − 20 |
|
|
x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ≥ |
20 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|||
|
x < 4 |
|
|
|
|
|
|
|
|
|
||||
|
x > 5 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
2 |
< x < 4, x > 5 . Ответ: |
2 |
2 |
; 4 |
(5; +∞) . |
|
|||||||
|
|
|
||||||||||||
|
9 |
|
|
|
|
9 |
|
|
|
|
|
|
||

Краткий курс школьной математики |
107 |
|
|
p 5
p 6
p 7

 5x − x2 > x − 2
5x − x2 > x − 2
Решение:
а) Так как D (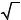 ) = [0; +∞ ) и E (
) = [0; +∞ ) и E (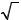 ) = [0; +∞ ) , то если левая
) = [0; +∞ ) , то если левая
часть неравенства неотрицательная, а правая отрицательная, то неравенство верно, отсюда имеем:
5x − x2 |
≥ 0 |
x2 |
− 5x ≤ 0 |
0 ≤ x ≤ 5 |
(0 ≤ x < 2) |
|
||
|
|
|
|
|
|
|
(1) |
|
x − 2 |
< 0 |
x |
< 2 |
x < 2 |
|
|
||
б) Если левая и правая части неравенства неотрицательны и с учетом D (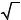 ) и E (
) и E ( ) , то возведем в квадрат обе части нера-
) , то возведем в квадрат обе части нера-
|
|
|
|
|
x |
− |
x2 |
> 0 |
|
0 < |
x |
< 5 |
|
|
|
|
|
|
5 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
венства, получим: x − 2 ≥ 0 |
|
x |
≥ 2 |
|
|||||||||
|
|
|
|
|
|
|
2 |
2 |
− 4 x + 4 |
|
2 |
− 9 x + 4 < 0 |
|
|
|
|
|
|
5x |
− x |
> x |
2 x |
|||||
2 x2 − 9 x + 4 = 0 |
|
|
|
|
|
|
|
|
|
|
|||
D = 81 − 32 = 49 |
|
|
|
|
|
|
|
|
|
||||
x = 9 − 7 |
= 1 ; x = 9 + 7 = 4 |
|
|
|
|
|
|
||||||
1 |
4 |
|
2 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 ≤ x < 5 |
|
|
|
|
|
|
|
|
|
|||
Имеем: |
1 |
< x |
< 4 |
(2 ≤ x < 4) |
|
|
|
|
(2) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Из (1) и (2) получим: 0 ≤ x < 4 Ответ: [0; 4) .

 2 x2 + 5x − 7 > 0 x + 6
2 x2 + 5x − 7 > 0 x + 6
Решение: |
|
|
|
|
|
|||||||
Так как D ( |
|
) = [0; +∞ ) и E ( |
|
|
) = [0; +∞ ) , то |
|||||||
|
|
|||||||||||
2 x2 |
|
|
|
|
|
|
|
x ≤ −3, 5 |
|
|
−6 < x ≤ −3, 5 |
|
|
+ 5x − 7 ≥ 0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x ≥ 1 |
|
|||
x + 6 > 0 |
|
|
|
|
x ≥ 1 |
|||||||
|
|
|
|
|
|
|
|
x > −6 |
|
|
|
|
Ответ: (−6; −3, 5] [1; +∞) . |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
1 − |
|
x − 2 |
|
> 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
2 − |
|
x −1 |
|
|
|
|
|
||||
108 |
|
|
|
|
В.А.Битнер |
|
|
|
|
|
|
Решение: |
|
|
|
||
|
|
|
x − 2 ≥ 0 |
|
|
а) С учетом D ( ) |
|
||||
имеем |
( x ≥ 2) |
(1) |
|||
|
|
|
x −1 |
≥ 0 |
|
б) найдем нули числителя и знаменателя:
1 − 
 x − 2 = 0, x = 3; 2 −
x − 2 = 0, x = 3; 2 − 
 x −1 = 0, x = 5 и решим неравенство методом интервалов с учетом (1)
x −1 = 0, x = 5 и решим неравенство методом интервалов с учетом (1)
2 < x < 3, x > 5
Ответ: [2; 3) (5; +∞) .
p 8 |
3 |
|
|
|
5 |
|
|
|
|
x − 3 |
|
5 |
− x ≥ 0 |
||||||
|
|
|
|||||||
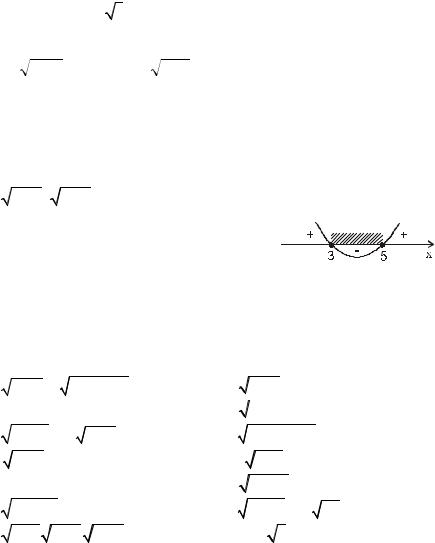
Решение:
( x − 3) (5 − x ) ≥ 0 ( x − 3) ( x − 5) ≤ 0
Ответ: [3; 5] .
Упражнения для самостоятельного решения.
Решить уравнения:
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 4 ≤ x2 + x + 3 |
|
|
x − 2 − 3 |
> 0 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 3 − 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 42 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
4 − x2 > − 3 − x |
|
|
x2 + 5x + 7 < 3 + x |
|||||||||||||||||||||||||||
p 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 62 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x − 2 − 2 |
|
|
|
|
|
|
|
|
x −1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
< 0 |
|
|
|
|
|
|
≥ 0 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− x + 5 |
|||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
7 |
|
|
4 x − x > x − 5 |
8 |
|
|
6 − x > − − x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
p 9 |
|
|
|
|
|
|
|
|
p 102 x − 3 |
|
− 5 ≤ 0 |
|||||||||||||||||||||
|
3 x −1 5 5 − x x − 2 > 0 |
x |
||||||||||||||||||||||||||||||
Ответы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
p 1 |
[−4; −1] [1; +∞ ) |
p 22 |
[3; 7 ) (11; +∞ ) |
|||||||||||||||||||||||||||||
p 3 |
[−2; 2] |
p 42 |
(−2; +∞) |
|
|
|
|
|
|
|||||||||||||||||||||||
p 5 |
[2; 6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
p 62 |
[1; 5) |
|
|
|
|
|
|
|
|
|
|
||||||

Краткий курс школьной математики |
|
|
|
|
109 |
|
|
|
|
|
|
|
|
p 7 |
[0; 4] |
p 82 |
− |
|
; 0 |
|
6 |
||||||
|
|
|
|
|
||
p 9 |
[2; 5] |
p 102 [0; 25] |
|
|||
Тема XVII. Системы линейных уравнений и методы их решения. Правила Крамера. Метод Гаусса.
(1)Системы 2 линейных уравнений с 2 неизвестными и ме- тоды их решения.
o 1 |
|
Уравнение вида a x + a x |
+ …+ a x |
= b , где |
a , a ,…, a - не- |
||||
|
|
1 1 2 2 |
|
n |
n |
|
1 |
2 |
n |
|
|
которые постоянные действительные числа, называется линей- |
|||||||
|
|
ным уравнением с n неизвестными x , x ,…, x . |
|
|
|||||
|
|
|
|
|
1 |
2 |
n |
|
|
o 2 |
|
a x + b y = c |
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
Система уравнений вида |
1 |
1 |
1 |
|
|
|
(1), |
|
|
a2 x + b2 y = c2 |
|
|
|
|
|||
|
|
где a1 , a2 , b1 , b2 , c1 , c2 R , |
называется |
системой |
2 |
линейных |
|||
|
|
уравнений с 2 неизвестными x и y . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
o 3 |
|
Система линейных уравнений называется совместной, если она |
|
|
имеет решение. |
o 4 |
|
Система линейных уравнений называется несовместной, если |
|
||
|
|
она не имеет решений. |
o 5 |
|
Система линейных уравнений называется определенной, если |
|
||
|
|
она имеет единственное решение. |
o 6 |
|
Система линейных уравнений называется неопределенной, ес- |
|
||
|
|
ли она имеет бесконечно много решений. |
110 |
В.А.Битнер |
|
|
Способы решения.
1)Способ подстановки – в одном из уравнений системы одно неизвестное выражается через другое неизвестное и подставляется в другое уравнение системы.
p 1 |
|
|
x = |
8 − 3 y |
|
|
|
24 − 9 y + 4 y = 14 |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
2x + 3 y = 8 |
|
|
|
x = 1 |
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
8 − 3 y |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3x + 2 y = 7 |
|
|
|
8 − 3 y |
|
|
|
|
x = |
|
|
|
|
|
y = 2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3 |
|
|
+ 2 y |
= 7 |
|
2 |
|
|
|
|
|
|||||
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Ответ: {(1; 2)} . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
Способ алгебраического сложения. |
|
|
|
|
|
|
|
|
|
|||||||||
p 2 |
2x + 3 y = 8 |
|
|
6x + 9 y = 24 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 2 y = 7 |
|
|
6x + 4 y = 14 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
7 − 2 y |
|
7 − 4 |
|
|
|
||||
|
|
|
|
|
|
5 y = 10 |
|
|
x = |
= |
= 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
||||
y = 2
Ответ: {(1; 2)} .
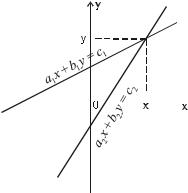
(2)Геометрическая интерпретация решения систем 2
линейных уравнений с 2 неизвестными.
Линейное уравнение с двумя неизвестными является линейной функцией, графиком которой служит прямая. По-  этому решение системы 2 линейных уравнений с 2 неизвестными имеет следующую геометрическую интерпретацию.
этому решение системы 2 линейных уравнений с 2 неизвестными имеет следующую геометрическую интерпретацию.
1.Система имеет единственное решение – прямые пересекаются в точке ( x; y ) .
