6. Задачі оптимізації

• Задачі оптимізації;

• функції maximize( ) й minimize( );

• лінійне програмування (ЛП);

• задача оптимального завантаження виробничих потужностей;

• транспортна задача (відкрита, закрита);

• цілочислове програмування;

• задача про комівояжера;

• нелінійне програмування (НЛП).

1. Пошук екстремумів функцій

Термін оптимізація має дуже широкий ужиток, а тому може залежати від контексту. Будемо розуміти оптимізацію як процес знаходження екстремуму (максимального або мінімального значення) економічних функцій, тобто вибір найкращого варіанта з можливих.

У MathCAD існують дві функції спеціально для пошуку максимумів і мінімумів – maximize( ) та minimize( ). Перед використанням цих функцій треба присвоїти початкове значення (наближення) аргументу функції, що оптимізується. Загальний вигляд функцій: maximize (f, x₁, x₂,…), де f – назва функції f(x₁, x₂,…), що максимізується, а x₁, x₂, … – аргументи, за якими шукається максимум (аналогічно для мінімуму).

Якщо в задачі є обмеження, то їх треба зазначити перед викликом цих функцій, попередивши їх ключовим словом given.

Можливість запису перед функціями maximize( ) та minimize( ) системи обмежень у вигляді нерівностей і рівностей дозволяє розв’язувати в середовищі MathCAD широкий клас оптимізаційних задач під назвою задачі лінійного програмування.

2. ЗадаЧі лінійного, нелінійного, цілочислового програмування

Задача лінійного програмування (ЛП) у загальному вигляді формулюється в такий спосіб:

потрібно знайти екстремум (мінімум або максимум) цільової функції

за обмежень:

,

де c_j – витрати або прибуток (у випадку мінімізації або максимізації відповідно);

a_ij – питомі витрати i-го ресурсу на одиницю випуску j-го продукту;

b_i – ліміти ресурсів або кількісне вираження попиту;

(a_ij, b_i, c_j – задані числові значення)

x_j – шукані кількості j-го продукту;

f(x₁,…, x_n) називається цільовою функцією.

Обмеження говорять про таке: у випадку мінімізаційної задачі (за обмеженості ресурсів) витрата ресурсів не може перевищувати їх наявність; у випадку максимізаційної задачі: потреби (попит) повинні бути цілком задоволені або перевищені.

У тому випадку, якщо обмеження задачі записані у вигляді рівностей (рівнянь), задача називається канонічною.

До задач ЛП відносяться задачі планування виробництва (задачі про використання ресурсів), задачі про суміші (про упорядкування раціону), про використання потужностей (про завантаження устаткування) тощо.

Однією із задач ЛП, що часто зустрічаються, є задача з розробки раціонального плану транспортних перевезень – так звана транспортна задача. Метою організації перевезень при цьому зазвичай є мінімізація витрат.

У загальному вигляді транспортна задача формулюється таким чином: потрібно перевезти певну кількість деяких вантажів із m пунктів відправлення до n пунктів призначення. При цьому необхідно мінімізувати сукупні витрати на транспортування всіх партій вантажу:

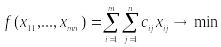
Обмеження

описують вимоги того, що весь вантаж має бути вивезений, а обмеження:

вимоги того, що має бути задоволена потреба у вантажах в кожному пункті призначення. Крім того, кількість перевезеного вантажу не може бути від’ємною:

де c_ij – витрати на транспортування одиниці вантажу з і-го пункту відправлення до j-го пункту призначення;

a_i – загальна кількість вантажу в i-му пункті відправлення;

b_j – загальна потреба у вантажі в j-му пункті призначення;

x_ij – кількість вантажу, перевезеного з i-го пункту відправлення до

j -го пункту призначення (невідомі величини, які треба знайти).

Якщо виконується умова:

(сумарна наявність вантажу збігається із сумарною потребою), то транспортна задача називається закритою. Інакше транспортна задача – відкрита. Розв’язання відкритої транспортної задачі в математиці зазвичай зводиться до розв’язання закритої задачі шляхом уведення ще одного (фіктивного) пункту призначення або споживання, який бере на себе різницю між наявністю вантажу й потребою. Однак для Excel або MathCAD відкритість або закритість задачі не є принциповим моментом.

Ще одна типова задача ЛП – задача оптимального завантаження виробничих потужностей. Постановка цієї задачі залежить від того, взаємозамінні чи ні розглянуті групи устаткування.

Якщо групи устаткування не взаємозамінні, то задаються а_ij – коефіцієнти витрат часу на обробку на i-му устаткуванні j-х виробів (деталей, вузлів), А_i – фонд часу по кожній групі устаткування у верстато- або машино-годинах, с_j – ефективність виробництва j-го виробу, а також часто зазначаються мінімально необхідні потреби в j-х виробах (В_mj) та верхні обмеження випуску (B_Mj), обумовлювані лімітами на матеріали. Шукане число виробів, оброблюваних на устаткуванні, приймається за x_j.

Тоді модель ЛП для невзаємозамінних груп устаткування буде мати вигляд:

, j=1,…,m

B_mj≤x_j≤B_Mj, j=1,…,m

Різновидом задачі ЛП є цілочислова задача, у якій всі елементи x_i – цілі числа. Класичним прикладом цілочислової задачі є задача про комівояжера (задача про призначення, про розподіл замовлень, розстановку персоналу тощо). Задачу про комівояжера можна застосувати при визначенні оптимальної послідовності обробки деталей, розвезення товарів, підведення електроенергії до робочих місць тощо.

Для розв’язання задачі про комівояжера за невідомі приймаються змінні x_ij, рівні або 1 (i-а деталь оброблюється на j-му верстаті), або 0 (не оброблюється). У матриці, складеній з таких змінних x_ij, у кожному рядку й у кожному стовпці має міститися рівно по одній одиниці.

На жаль, MathCAD не вміє розв’язувати задачі цілочислового програмування. Однак, як у Excel, до нього можна підключити пакет аналізу Solving and Optimization Extension Pack (Expert Solver), який надасть цю й багато інших додаткових можливостей розв’язання оптимізаційних задач.

Задачі лінійного програмування (ЛП) – окремий випадок задач нелінійного програмування (НЛП). В останніх і цільова функція, й обмеження можуть бути нелінійними функціями. Узагальнено задача НЛП має вигляд:

F(x₁,…, x_n)  max(min);

g_i(x₁,…, x_n)≤b_i, i=1,…,m;

x_j≥0, j=1,…,n.