- •Рисуночек(pict002)
- •7)Задача про роботу силового поля. Робота силового поля обчислюється двома шляхами: 1)в основу покладена властивість адитивності 2)основою даного розв’язку є формула Гріна: , де ;
- •4)Теор про середнє значення функції для потрійного інтегралу. Якщо функція f(X,y,z) – неперервна в замкнутій області , то існує точка в якій
- •9)Потрійні інтеграли у сферичних координатах. З маємо Отже, Обчислюємо якобіан переходу
- •10)Застосування потрійних інтегралів у геометрії та механіці. 1)Обчислення об’єму тіла.Якщо тіло однорідне і густина то об’єм дорівнює :
- •2)Координати центра мас тіла:
- •3)Момент інерції тіла відносно координатних осей:
- •2) Комплексні числа в тригонометричній та показниковій формах.
- •6)Основні властивості інтеграла від фкз, теорема Коші. Вони випливають з означення цього інтеграла:
- •Довжина .
- •1) Властивість лінійності перетворення Лапласа. Зображення функцій . T.Якщо , ,а і дійсні сталі то, ;і взагалі
- •7) Теор про інтегрування оригіналу.
6)Заміна
змінних у подвійному інтегралі. Полярні
координати, узагальнені полярні
координати.
Нехай функції x=φ(uv);y=ψ(uv)
неперервні і мають похідні у деякій
області
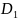 .
Ці функції встановлюють взаємооднозначну
відповідність між областями D
і
.
.
Ці функції встановлюють взаємооднозначну
відповідність між областями D
і
. ,
,
 - формула Остроградського.Полярні
координати.
- формула Остроградського.Полярні
координати. ;
;
 ;
;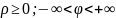 .
Тут роль u
виконує
.
Тут роль u
виконує
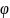 ,
а роль v
–
,
а роль v
–
 .Якобіан
переходу до полярних координат
.Якобіан
переходу до полярних координат
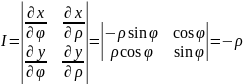 ;
;
 .
Тоді маємо:
.
Тоді маємо:
 .
У полярних координатах маємо площу
фігури
.
У полярних координатах маємо площу
фігури
 .Узагальнені
пол. коорд.
.Узагальнені
пол. коорд.
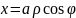 ;
;
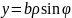 ;
.
;
.
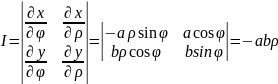 .
.
 .
Ці
координати застосовуються тоді, коли
область інтегрування є еліпс, або його
частина
.
Ці
координати застосовуються тоді, коли
область інтегрування є еліпс, або його
частина
5)Обчислення
подвійного інтегралу у декартовій
системі координат.
Область
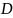 називається правильною у напрямі
якої-небудь осі, якщо пряма лінія, що
паралельна цій осі перетинає границю
області
не більше ніж у 2х точках. Подвійний
інтеграл від неперервної функції
називається правильною у напрямі
якої-небудь осі, якщо пряма лінія, що
паралельна цій осі перетинає границю
області
не більше ніж у 2х точках. Подвійний
інтеграл від неперервної функції
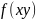 по правильній області
,
дорівнює двократному(повторному)
інтегралу по цій області:
по правильній області
,
дорівнює двократному(повторному)
інтегралу по цій області: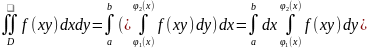 .
Обчислимо об’єм тіла іншим способом,
а саме за допомогою поперечних перерізів
площинами, які перпендикулярні OX.
.
Обчислимо об’єм тіла іншим способом,
а саме за допомогою поперечних перерізів
площинами, які перпендикулярні OX.
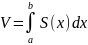 ,
при
,
при
 одержуємо криволінійну трапецію, яка
обмежена зверху кривою
одержуємо криволінійну трапецію, яка
обмежена зверху кривою
 .
Тоді
.
Тоді
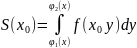 ,
у загальному випадку маємо
,
у загальному випадку маємо
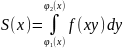 ,
,

4)Теорема
про оцінку подвійного інтеграла, теор
про середній подвійний інтеграл.
Теорема про оцінку. Нехай
функція f(x;y)
неперервна в області D,
тоді мають місце нерівності
 (1), де
(1), де
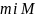 найменше і найбільше значення
в області
,
найменше і найбільше значення
в області
,
 площа області
.Доведення.
Відмітимо, що коли
площа області
.Доведення.
Відмітимо, що коли
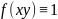 ,
то відповідний подвійний інтеграл є
площа області
,
тобто
,
то відповідний подвійний інтеграл є
площа області
,
тобто
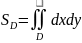 .
Згідно теореми Веєрштрассе всяка
неперервна у замкненій області функція
приймає свої найбільше і найменше
значення. Маємо
.
Згідно теореми Веєрштрассе всяка
неперервна у замкненій області функція
приймає свої найбільше і найменше
значення. Маємо
 .
.
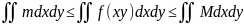 .
.
Геометричний
зміст даної теореми:
об’єм циліндричного тіла знаходиться
між об’ємами 2х циліндрів, які мають
ту ж основу – область
і висоти m
і
M.Теор
про середній подвійний інтеграл. Нехай
функція f(x;y)
неперервна в області D,
тоді має місце рівність
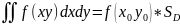 ,
,
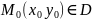 .Доведення:
для
неперервної функції
в замкненій області
знайдеться така точка
.Доведення:
для
неперервної функції
в замкненій області
знайдеться така точка
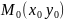 ,
що значення функції в цій точці
,
що значення функції в цій точці
 співпадає з заданим числом
співпадає з заданим числом
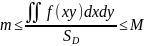 ;
;
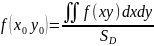 .
Геометричний зміст цієї теореми –
об’єм циліндроїда дорівнює об’єму
циліндра з висотою
.
Геометричний зміст цієї теореми –
об’єм циліндроїда дорівнює об’єму
циліндра з висотою
3)
Подвійний інтеграл – озн, властивості,
довести будь – яку одну властивість.
Озн. Нехай
функція f(x;y)
визначена в області D.
Аналогічно складемо інтегральну суму
 . якщо існую скінченна границя інтегральної
суми
. якщо існую скінченна границя інтегральної
суми
 коли
коли
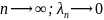 і ця границя не залежить від способу
поділу області D
на
і ця границя не залежить від способу
поділу області D
на
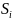 та вибору точок
та вибору точок
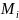 в
,
то f(x;y)
називається інтегрованою в області D,
а ця границя називається подвійним
інтегралом і позначається так:
в
,
то f(x;y)
називається інтегрованою в області D,
а ця границя називається подвійним
інтегралом і позначається так:

Властивості.
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
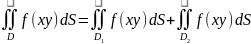 ,
при
,
при
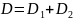 - адитивність. Границя між
і
- адитивність. Границя між
і
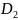 повинна бути гладкою лінією, Г.
якщо f(xy)≤
(xy)
в області
то
повинна бути гладкою лінією, Г.
якщо f(xy)≤
(xy)
в області
то
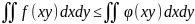
Доведення.
сталий
член можна виносити за знак інтегралу
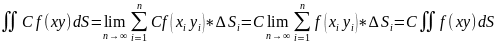
2)озн,
теор існування, геом. Зміст подвійного
інтегралу Озн.
Нехай функція f(x;y)
визначена в області D.
Аналогічно складемо інтегральну суму
. якщо існую скінченна границя інтегральної
суми
коли
і ця границя не залежить від способу
поділу області D
на
та вибору точок
в
,
то f(x;y)
називається інтегрованою в області D,
а ця границя називається подвійним
інтегралом і позначається так:
.Теорема
існування. (без дов)Якщо
f(x;y)
неперервна в області D,
то подвійний інтеграл існує.Геометричний
смисл. Якщо f(x;y)≥0
в області D,
то подвійний інтеграл
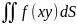 дорівнює об’єму тіла
дорівнює об’єму тіла
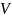
1)Задача,
яка приводить до поняття подвійного
інтеграла (обч об’єму тіла)
Нехай
в області D
задана
неперервна додатня функція z=f(x;y).
Треба знайти об’єм V
тіла обмеженого зверху поверхнею
z=f(x;y),
знизу областю D,
та циліндричною поверхнею, твірні якої
паралельні осі OZ.
Таке тіло називається циліндроїдом.
Розібємо область D
на елементарні
частинки
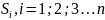 довільними лініями. Площу
однієй частинки позначимо
довільними лініями. Площу
однієй частинки позначимо
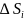 .
Всередині області
вибиремо довільну точку
.
Всередині області
вибиремо довільну точку
 .
Області
відповідає невелике циліндричне тіло,
обєм якого дорівнює
.
Області
відповідає невелике циліндричне тіло,
обєм якого дорівнює
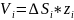 ;
;
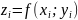 ,
тоді обєм даного тіла наближено дорівнює
,
тоді обєм даного тіла наближено дорівнює
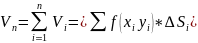 .Нехай
.Нехай
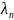 максимальний діаметр
го.
Очевидно, що
максимальний діаметр
го.
Очевидно, що
 тим точніше виражає обєм
,
чим більша
тим точніше виражає обєм
,
чим більша
 і чим менше
.
Озн1: під
обємом тіла будемо розуміти вираз
і чим менше
.
Озн1: під
обємом тіла будемо розуміти вираз
 .
.
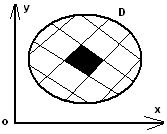

9)Моменти
інерції плоскої фігури. Формула Гріна
про зв'язок подвійного інтеграла 2го
роду вздовж замкненого контура L
та
подвійного інтеграла, обмеженого
областю D.
Моментом інерції
 ,
матеріальної точки
,
матеріальної точки
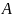 ,
що має масу m,
відносно деякої точки О називається
добуток маси m
на квадрат відстані від точки
до точки О
-
,
що має масу m,
відносно деякої точки О називається
добуток маси m
на квадрат відстані від точки
до точки О
-
 .
.
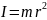 .
Елементарні
моменти інерції відносно координатних
осей:
.
Елементарні
моменти інерції відносно координатних
осей:
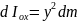 ;
;
 ;
Тоді моменти інерції всієї області
відносно координатних осей:
;
Тоді моменти інерції всієї області
відносно координатних осей:
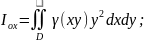
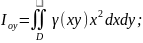 момент інерції відносно початку
координат:
момент інерції відносно початку
координат:
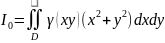 .
зауваження: якщо пластинка однорідна,
.
зауваження: якщо пластинка однорідна,
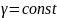 ,
то покладають
,
то покладають
 .Формула
Гріна: якщо
P
та Q
неперервно диференційовані в області
D,
яка обмежена гладкою кривою L,
то
.Формула
Гріна: якщо
P
та Q
неперервно диференційовані в області
D,
яка обмежена гладкою кривою L,
то
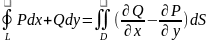 - формула Гріна.
Доведення:
- формула Гріна.
Доведення:
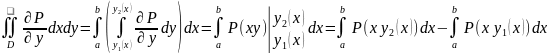 ;
кожен з цих інтегралів дорівнює
криволінійному інтегралу від функції
;
кожен з цих інтегралів дорівнює
криволінійному інтегралу від функції
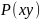 по відповідному шляху;
по відповідному шляху;
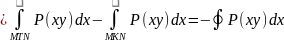 ;
Аналогічно
;
Аналогічно
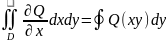 ;
Додаємо одержані рівності і одержуємо
формулу Гріна:
;
Додаємо одержані рівності і одержуємо
формулу Гріна:
![]()
7)Обчислення
об’єму тіла, площі фігури, площі
поверхні, за допомогою подвійного
інтеграла.
Обчислення об’єму тіла
Нехай тіло обмежено двома поверхнями
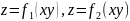 і циліндричною поверхнею. Тоді об’єм
такого тіла
і циліндричною поверхнею. Тоді об’єм
такого тіла
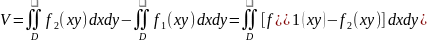 .
площа
фігури обчислюється
за формулою
.
площа
фігури обчислюється
за формулою
 .площі
поверхні
.площі
поверхні
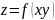 -
рівняння площі поверхні, де
-
рівняння площі поверхні, де
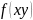 - неперервна і диференційована.
Використовуючи інтегральну суму можна
довести, що площа поверхні обчислюється
за формулою:
- неперервна і диференційована.
Використовуючи інтегральну суму можна
довести, що площа поверхні обчислюється
за формулою:
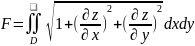
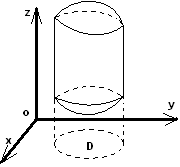
8)Маса
плоскої пластинки. Статичні моменти
пластинки. Координати центра мас
пластинки.
Розглянемо матеріальну плоску область
,
на якій розподілено деяку речовину з
густиною
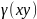 .
неперервна в області
.
Розіб’ємо область
на елементарні частинки лініями
.
неперервна в області
.
Розіб’ємо область
на елементарні частинки лініями
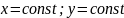 .
Тоді елементарна маса
.
Тоді елементарна маса
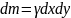 .
Елементарні
статичні моменти відносно координатних
осей визначаються рівностями
.
Елементарні
статичні моменти відносно координатних
осей визначаються рівностями
 ,
,
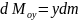 ,
тоді маса
,
тоді маса
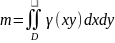 ;
;
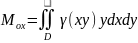 ;
;
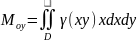 ;
згідно
означення центра мас системи матеріальних
точок виконуються такі співвідношення:
;
згідно
означення центра мас системи матеріальних
точок виконуються такі співвідношення:
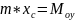 ;
;
 ;
отже
координати центра мас:
;
отже
координати центра мас:
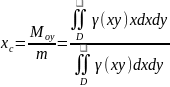 ;
;
 ;
зауваження:
якщо пластинка однорідна,
,
то покладають
.
;
зауваження:
якщо пластинка однорідна,
,
то покладають
.
1)Криволінійні
інтеграли 1го роду (по довжині дуги) –
озн та обчислення.
Нехай
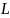 крива і на ній визначена функція
крива і на ній визначена функція
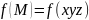 .
Складемо інтегральну суму:
для цього розбиваємо дугу
на частинки за допомогою точок
,
довжини яких -
.
Складемо інтегральну суму:
для цього розбиваємо дугу
на частинки за допомогою точок
,
довжини яких -
 ;
- максимальна
при 1≤i≤n.
Виберемо
на дузі
;
- максимальна
при 1≤i≤n.
Виберемо
на дузі
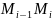 довільну
точку
довільну
точку
 і запишемо інтегральну суму:
і запишемо інтегральну суму:
 .Озн.
Скінченна
границя інтегральної суми
.Озн.
Скінченна
границя інтегральної суми
 при
при
 ;
;
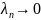 .
Якщо вона існує і не залежить від способу
ділення кривої на елементарні частини
та вибору точок
на них, називається криволінійним
інтегралом 1го роду від функції
.
Якщо вона існує і не залежить від способу
ділення кривої на елементарні частини
та вибору точок
на них, називається криволінійним
інтегралом 1го роду від функції
 по дузі
і позначається так:
по дузі
і позначається так:
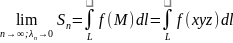 .
Відмітимо, що цей інтеграл не залежить
від напряму обходу дуги, тобто від шляху
інтегрування.Обчислення:
Нехай
крива
задана у параметричній формі
.
Відмітимо, що цей інтеграл не залежить
від напряму обходу дуги, тобто від шляху
інтегрування.Обчислення:
Нехай
крива
задана у параметричній формі
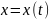 ;
;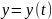 ;
;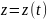 ;
;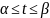 ;
;
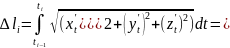 (скористаємось
теоремою про середнє для визначеного
інтегралу)
(скористаємось
теоремою про середнє для визначеного
інтегралу) ;
значенню
;
значенню
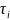 параметра
параметра
 відповідає точка
.
відповідає точка
.
 ;
одержали
інтегральну суму для функції
;
одержали
інтегральну суму для функції
 границя
цієї суми є криволінійний інтеграл 1го
роду
границя
цієї суми є криволінійний інтеграл 1го
роду
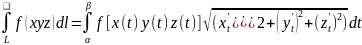 ;
;
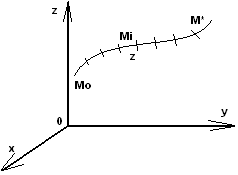
2)Задача про масу зігнутого
стержня. Нехай вздовж
просторової кривої
розподілена речовина з густиною
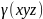 .
Треба знайти масу цієї кривої(тобто
зігнутого стержня). Для розвязання
задачі розділимо дугу
на n
елементарних частинок, довжини яких
позначимо
,
- максимальна
при 1≤i≤n.
Будемо вважати, що густина на відрізку
стала. Тоді її маса
.
Треба знайти масу цієї кривої(тобто
зігнутого стержня). Для розвязання
задачі розділимо дугу
на n
елементарних частинок, довжини яких
позначимо
,
- максимальна
при 1≤i≤n.
Будемо вважати, що густина на відрізку
стала. Тоді її маса
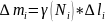 ,
де
- довільна точка дуги.
,
де
- довільна точка дуги.
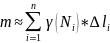 ;
;
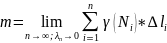 ;
ця границя є криволінійний
інтеграл 1го роду.
;
ця границя є криволінійний
інтеграл 1го роду.
3)Криволінійні
інтеграли 1го роду (по довжині дуги) –
озн, теор існування, властивості.
Нехай
крива і на ній визначена функція
.
Складемо інтегральну суму:
для цього розбиваємо дугу
на частинки за допомогою точок
,
довжини яких -
;
- максимальна
при 1≤i≤n.
Виберемо
на дузі
довільну
точку
і запишемо інтегральну суму:
.Озн.
Скінченна
границя інтегральної суми
при
;
.
Якщо вона існує і не залежить від способу
ділення кривої на елементарні частини
та вибору точок
на них, називається криволінійним
інтегралом 1го роду від функції
по дузі
і позначається так:
.
Відмітимо, що цей інтеграл не залежить
від напряму обходу дуги, тобто від шляху
інтегрування.Теор
існув. (без
дов) – якщо крива
гладка і функція
неперервна на ній, то криволінійний
інтеграл 1го роду існує на ній.Властивості.
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
якщо
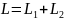 ,
то
,
то
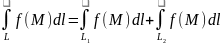 ;
Г.
не
залежить від вибору початкової точки
на замкненому контурі.
;
Г.
не
залежить від вибору початкової точки
на замкненому контурі.
4)Криволінійні інтеграли
2го роду (по координатам) – озн, теор
існування, властивості. Озн. Скінченна
границя інтегральної суми
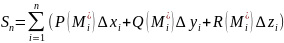 при
;
,
Скінченна границя інтегральної
суми
при
;
.
Якщо вона існує і не залежить від способу
ділення кривої на елементарні частини
та вибору точок
при
;
,
Скінченна границя інтегральної
суми
при
;
.
Якщо вона існує і не залежить від способу
ділення кривої на елементарні частини
та вибору точок
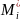 на них називається криволінійним
інтегралом 2го роду і позначається так:
на них називається криволінійним
інтегралом 2го роду і позначається так:
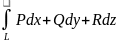 .
Цей інтеграл змінює свій знак при зміні
напряму шляху інтегрування.Теорема
існування. Якщо крива
гладка, а функції P,Q,R
– неперервні, то інтеграл існує.Властивості.
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
якщо
,
то
.
Цей інтеграл змінює свій знак при зміні
напряму шляху інтегрування.Теорема
існування. Якщо крива
гладка, а функції P,Q,R
– неперервні, то інтеграл існує.Властивості.
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
якщо
,
то
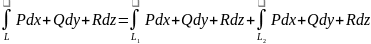 ;
;
5)Криволінійні інтеграли
2го роду (по координатам) – озн і
обчислення. Озн. Скінченна
границя інтегральної суми
при
;
,
Скінченна границя інтегральної
суми
при
;
.
Якщо вона існує і не залежить від способу
ділення кривої на елементарні частини
та вибору точок
на них називається криволінійним
інтегралом 2го роду і позначається так:
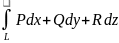 .
Цей інтеграл змінює свій знак при зміні
напряму шляху інтегрування.Обчисл.
Нехай
задана параметрично формі
;
;
;
,
використовуючи інтегральну суму можна
довести, що
.
Цей інтеграл змінює свій знак при зміні
напряму шляху інтегрування.Обчисл.
Нехай
задана параметрично формі
;
;
;
,
використовуючи інтегральну суму можна
довести, що
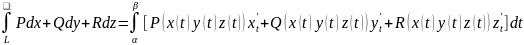 ;
якщо z=0, то
одержимо плоский випадок
;
якщо z=0, то
одержимо плоский випадок
 .
.
6)Криволінійні
інтеграли від повного диференціалу.
Виконання умови
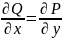 рівносильно тому, що вираз
рівносильно тому, що вираз
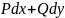 є повний диференціал деякої функції
є повний диференціал деякої функції
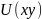 .
Тобто
.
Тобто
 .
В цьому випадку вектор
.
В цьому випадку вектор
 дорівнює
дорівнює
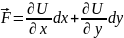 і є градієнт функції
.
і є градієнт функції
.
 ,
тоді функція
є потенціал векторного поля
,
тоді функція
є потенціал векторного поля
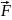 .Теорема:
нехай
,
тоді криволінійний інтеграл
по будь-якій кривій L
дорівнює різниці значень функції
в точках M
і N
(кінцях кривої L).
Тобто
.Теорема:
нехай
,
тоді криволінійний інтеграл
по будь-якій кривій L
дорівнює різниці значень функції
в точках M
і N
(кінцях кривої L).
Тобто
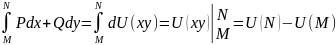 .Доведення:
нехай
L
задана параметрично
;
;
.Доведення:
нехай
L
задана параметрично
;
;
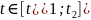 ,
причому точка M
відповідає
значенню параметра
,
причому точка M
відповідає
значенню параметра
 ,
а точка N
-
,
а точка N
-
 .
Тоді маємо
.
Тоді маємо
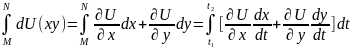 ,
вираз у квадратних дужках є повна
похідна по t.
,
вираз у квадратних дужках є повна
похідна по t.
 .
Отже криволінійний інтеграл від повного
диференціала не залежить від форми
кривої, по якій проводиться інтегрування.
.
Отже криволінійний інтеграл від повного
диференціала не залежить від форми
кривої, по якій проводиться інтегрування.
7)Поверхневий
інтеграл 1го роду – озн, властивості,
фізичний смисл та обчислення.
Поверхневий інтеграл 1го роду є
узагальнення криволінійного інтегралу
1го роду на випадок простору. Нехай
функція
неперервна і задана на поверхні S.
 - рівняння гладенької поверхні S.
Складемо інтегральну суму
.
Для цього розділимо поверхню на
елементарні частини
,
1=1;2;3…n.
- площа кожної із них, λ – максимальне
значення
при i=[1…n].
На
вибираємо довільні точки з координатами
- рівняння гладенької поверхні S.
Складемо інтегральну суму
.
Для цього розділимо поверхню на
елементарні частини
,
1=1;2;3…n.
- площа кожної із них, λ – максимальне
значення
при i=[1…n].
На
вибираємо довільні точки з координатами
 .
.
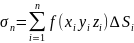 .
Озн.
Границя
інтегральної суми
,
при
.
Озн.
Границя
інтегральної суми
,
при
 називається
поверхневим інтегралом 1го роду від
функції
по поверхні S.
Тобто
називається
поверхневим інтегралом 1го роду від
функції
по поверхні S.
Тобто
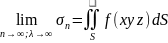 .
Властивості:
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
якщо
.
Властивості:
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
якщо
 ,
то
,
то
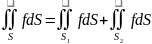 .Фізичний
смисл: якщо
функція
.Фізичний
смисл: якщо
функція
 на поверхні S,
то цей інтеграл виражає собою масу
матеріальної поверхні S,
густина в кожній точці якої дорівнює
.
За допомогою поверхневого інтеграла
1го роду можна також обчислити статичні
моменти та координати центра мас
поверхні.
на поверхні S,
то цей інтеграл виражає собою масу
матеріальної поверхні S,
густина в кожній точці якої дорівнює
.
За допомогою поверхневого інтеграла
1го роду можна також обчислити статичні
моменти та координати центра мас
поверхні.
Обчислення:
нехай
поверхня S
проектується
однозначно на XOY
в деяку область
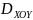 ,
це означає, що пряма лінія паралельна
осі OZ
перетинає таку поверхню тільки в одній
точці. Можна довести, що в цьому випадку
має місце формула:
,
це означає, що пряма лінія паралельна
осі OZ
перетинає таку поверхню тільки в одній
точці. Можна довести, що в цьому випадку
має місце формула:
 .
.
8)Поверхневий
інтеграл 2го роду – озн, властивості,
фізичний смисл та обчислення.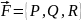 ,
P,Q,R
– неперервні
функції, які задані на поверхні
,
P,Q,R
– неперервні
функції, які задані на поверхні
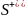 додатній
стороні поверхні S.
Поверхня
характеризується напрямком нормалі
додатній
стороні поверхні S.
Поверхня
характеризується напрямком нормалі
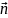 ,
,
 .
Побудуємо
інтегральну суму. Для цього розділимо
S
на
елементарні частинки
,
з точками
і
знайдемо вектор
.
Побудуємо
інтегральну суму. Для цього розділимо
S
на
елементарні частинки
,
з точками
і
знайдемо вектор
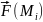 .
Фізичний смисл:
Складемо
добуток скалярного добутка на площу
поверхні:
.
Фізичний смисл:
Складемо
добуток скалярного добутка на площу
поверхні:
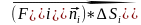 .
Якщо
- швидкість рідини, що протікає через
поверхню S,
то цей добуток дорівнює кількості
рідини, що протікає через
за одиницю часу у напрямі вектора
- це потік векторного поля через поверхню
S.Озн.
Поверхневим
інтегралом 2го роду називається
.
Якщо
- швидкість рідини, що протікає через
поверхню S,
то цей добуток дорівнює кількості
рідини, що протікає через
за одиницю часу у напрямі вектора
- це потік векторного поля через поверхню
S.Озн.
Поверхневим
інтегралом 2го роду називається
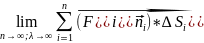 ;
і позначається так:
;
і позначається так:
 ,
або в координатній формі
,
або в координатній формі
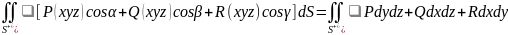 .Властивості:
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
якщо
,
то
.Властивості:
А.
інтеграл від суми дорівнює сумі
інтегралів, Б.
сталий член можна виносити за знак
інтегралу, В.
якщо
,
то
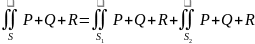 .Обчислення
– поверхневий
інтеграл 2го роду обчислюється за
допомогою подвійних інтегралів по
відповідним областям.
.Обчислення
– поверхневий
інтеграл 2го роду обчислюється за
допомогою подвійних інтегралів по
відповідним областям.
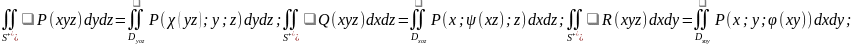 рисуночек(pict001)
рисуночек(pict001)
9)Умови
незалежності криволінійного інтеграла
2го роду (по координатам) від форми шляху
інтегрування.
Розглянемо криволінійний інтеграл
вздовж довільної кривої L,
яка з’єднує M
i
N:
 (1). Будемо вважати, що функції P,Q,
(1). Будемо вважати, що функції P,Q,
 -
неперервні в області D,
яка містить
L.
Виникає питання – при яких умовах цей
інтеграл не залежить від форми кривої
L,
а залежить тільки від положення точок
M
i
N?
Розглянемо дві довільні криві, які
з’єднують M
і N
і лежать в області D.
Нехай криволінійний інтеграл (1) не
залежить від шляху інтегрування, тобто
-
неперервні в області D,
яка містить
L.
Виникає питання – при яких умовах цей
інтеграл не залежить від форми кривої
L,
а залежить тільки від положення точок
M
i
N?
Розглянемо дві довільні криві, які
з’єднують M
і N
і лежать в області D.
Нехай криволінійний інтеграл (1) не
залежить від шляху інтегрування, тобто
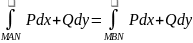 .
Звідки маємо:
.
Звідки маємо:
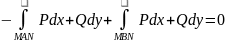 .
.
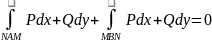 .
.
 ;
L=MBNAM.
Тобто криволінійний інтеграл будь-якого
замкненого контуру, що лежить в області
D,
=0. Має місце і обернене твердження –
якщо криволінійний інтеграл по замкненому
контуру =0, то він не залежить від вибору
шляху інтегрування. Якими ж умовами
повинні задовольняти функції P
i
Q,
щоб криволінійний інтеграл по замкненому
контуру = 0? Має місце така теорема: нехай
функції P
i
Q
неперервні в D,
тоді для того, щоб криволінійний інтеграл
по будь-якому замкненому контуру L,
LєD,
=0, тобто
;
L=MBNAM.
Тобто криволінійний інтеграл будь-якого
замкненого контуру, що лежить в області
D,
=0. Має місце і обернене твердження –
якщо криволінійний інтеграл по замкненому
контуру =0, то він не залежить від вибору
шляху інтегрування. Якими ж умовами
повинні задовольняти функції P
i
Q,
щоб криволінійний інтеграл по замкненому
контуру = 0? Має місце така теорема: нехай
функції P
i
Q
неперервні в D,
тоді для того, щоб криволінійний інтеграл
по будь-якому замкненому контуру L,
LєD,
=0, тобто
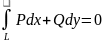 (2), необхідно і достатньо, щоб виконувалась
умова ,
(3), у всіх точках в області D.Достатність:
розглянемо
формулу Гріна для довільного замкненого
контуру L,
LєD:
(2), необхідно і достатньо, щоб виконувалась
умова ,
(3), у всіх точках в області D.Достатність:
розглянемо
формулу Гріна для довільного замкненого
контуру L,
LєD:
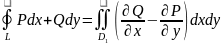 ,
якщо скористатися умовою (3), то подвійний
інтеграл тотожно=0:
.
,
якщо скористатися умовою (3), то подвійний
інтеграл тотожно=0:
.
Необхідність:
нехай виконується (2). Доведемо (3) від
супротивного. Припустимо ,
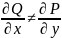 хоча б в одній точці. Нехай в точці
хоча б в одній точці. Нехай в точці
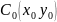 має місце нерівність
має місце нерівність
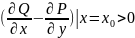 .
Так як функції
- неперервні, то в деякому околі
.
Так як функції
- неперервні, то в деякому околі
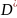 точки
точки
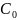 маємо:
маємо:
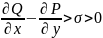 .
Тоді:
.
Тоді:
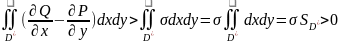 .
З формули Гріна випливає, що криволінійний
інтеграл теж >0,
а це суперечить умові (2), отже умова (2)
виконується у всіх точках області D.
Необхідність доведена.
.
З формули Гріна випливає, що криволінійний
інтеграл теж >0,
а це суперечить умові (2), отже умова (2)
виконується у всіх точках області D.
Необхідність доведена.
Рисуночек(pict002)
10)Обчислення
площі плоскої фігури за допомогою
криволінійного інтеграла 2го роду.
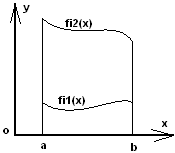
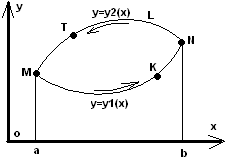
Нехай задана правильна область D
обмежена замкненою кривою L.
Ця область проектується на ох у відрізок
ab
і обмежена лініями y=y1(x);y=y2(x);
причому y1(x)<y2(x).
Тоді площа фігури D
дорівнює
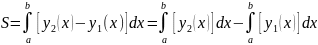 ;
але перший інтеграл = криволінійному
інтегралу по кривій NTM.
;
але перший інтеграл = криволінійному
інтегралу по кривій NTM.
 ;
другий інтеграл =
;
другий інтеграл =
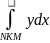 ,
виберемо напрям інтегрування як показано
на рисунку, тоді
,
виберемо напрям інтегрування як показано
на рисунку, тоді
 ;
;
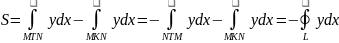 - циркуляція по контуру. Аналогічно
можна довести і іншу формулу:
- циркуляція по контуру. Аналогічно
можна довести і іншу формулу:
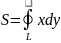 ;
на
практиці
;
на
практиці
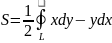 ;
;
1)Скалярне поле – озн,
приклади, геометричні характеристики.
Озн: частина
простору або весь простір в кожній
точці якого визначена деяка величина,
називається полем цієї величини. Якщо
величина скалярна, то і поле називається
скалярним. Наприклад, а) скалярне поле
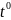 у просторі, де знаходиться нагріте
тіло, б) скалярне поле електричного
потенціала у просторі навколо електричного
заряду і тд. Якщо скалярна функція
U(xyz)
не залежить від часу, то таке поле
називається стаціонарним.Геометричні
характеристики: важливою
характеристикою є поверхня рівня:
U(xyz)=C.
У випадку площини маємо лінії рівня –
U(xy)=C.
Наприклад, лінії висот точок земної
поверхні над рівнем моря (топографія).
у просторі, де знаходиться нагріте
тіло, б) скалярне поле електричного
потенціала у просторі навколо електричного
заряду і тд. Якщо скалярна функція
U(xyz)
не залежить від часу, то таке поле
називається стаціонарним.Геометричні
характеристики: важливою
характеристикою є поверхня рівня:
U(xyz)=C.
У випадку площини маємо лінії рівня –
U(xy)=C.
Наприклад, лінії висот точок земної
поверхні над рівнем моря (топографія).
2)Скалярне
поле – озн, диференціальні характеристики,
оператори Гамільтона. Озн:
частина простору або весь простір в
кожній точці якого визначена деяка
величина, називається полем цієї
величини. Якщо величина скалярна, то і
поле називається скалярним. Наприклад,
а) скалярне поле
у просторі, де знаходиться нагріте
тіло, б) скалярне поле електричного
потенціала у просторі навколо електричного
заряду і тд. Якщо скалярна функція
U(xyz)
не залежить від часу, то таке поле
називається стаціонарним.Диференціальні
характеристики: 1ою
такою характеристикою є швидкість
зміни U(xyz)
при переміщенні даної точки у різні
напрями у просторі. Ця швидкість дорівнює
похідній за напрямком:
 ;
;
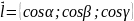 .
У випадку площини
.
У випадку площини
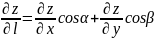 .
2ою
характеристикою є градієнт:
.
2ою
характеристикою є градієнт:
 ,
для площини z=f(xy),
,
для площини z=f(xy),
 .
Похідна
за напрямом і градієнт зв’язані між
собою співвідношенням:
.
Похідна
за напрямом і градієнт зв’язані між
собою співвідношенням:
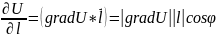 .
Модуль градієнта дорівнює найбільшому
значенню похідної за напрямком від
функції U(xyz)
у даній точці М, а напрям співпадає з
вектором нормалі до поверхні рівня в
цій точці. Оператор
Гамільтона:
для
позначення градієнта та інших величин
в теорії поля часто використовується
символічний вектор набла , що був
введений Гамільтоном, він позначається
так:
.
Модуль градієнта дорівнює найбільшому
значенню похідної за напрямком від
функції U(xyz)
у даній точці М, а напрям співпадає з
вектором нормалі до поверхні рівня в
цій точці. Оператор
Гамільтона:
для
позначення градієнта та інших величин
в теорії поля часто використовується
символічний вектор набла , що був
введений Гамільтоном, він позначається
так:
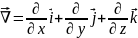 .
Тоді
.
Тоді
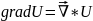 .
Слово набла в перекладі з грецької –
арфа.
.
Слово набла в перекладі з грецької –
арфа.
3)Векторне
поле – озн, приклади, геометричні
характеристики. Озн:
частина
простору або весь простір, в кожній
точці якого визначений вектор
 ,
називається полем цього вектора, коротше
– векторним полем. Наприклад, а) у
просторі навколо Землі існує стаціонарне
гравітаційне векторне поле, на матеріальну
точку М, що знаходиться в цьому просторі
діє сила тяжіння
,
називається полем цього вектора, коротше
– векторним полем. Наприклад, а) у
просторі навколо Землі існує стаціонарне
гравітаційне векторне поле, на матеріальну
точку М, що знаходиться в цьому просторі
діє сила тяжіння
 ,
яка практично не залежить від часу, б)
навколо тіла, що має електричний заряд
маємо векторне поле напруги, яка проявляє
себе по відношенню до зарядженої
частинки, внесеної в це поле, в) нехай
в деяку просторову область Ω протікає
рідина зі швидкістю
,
яка практично не залежить від часу, б)
навколо тіла, що має електричний заряд
маємо векторне поле напруги, яка проявляє
себе по відношенню до зарядженої
частинки, внесеної в це поле, в) нехай
в деяку просторову область Ω протікає
рідина зі швидкістю
 ,
тоді маємо гідродинамічне стаціонарне
поле швидкостей
рідини, що протікає.Геометричні
характеристики: це
векторні лінії та векторні трубки.
Векторною лінією називається крива,
дотична в кожній точці якої співпадає
з напрямом вектора поля в цій же точці.
Якщо
,
тоді маємо гідродинамічне стаціонарне
поле швидкостей
рідини, що протікає.Геометричні
характеристики: це
векторні лінії та векторні трубки.
Векторною лінією називається крива,
дотична в кожній точці якої співпадає
з напрямом вектора поля в цій же точці.
Якщо
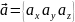 ,
то диференціальні рівняння векторних
ліній мають вигляд:
,
то диференціальні рівняння векторних
ліній мають вигляд:
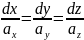 .
Векторною трубкою називається поверхня,
утворена векторними лініями, що проходять
через точки замкненої кривої. Ця крива
не повинна співпадати з якою-небудь
векторною лінією.
.
Векторною трубкою називається поверхня,
утворена векторними лініями, що проходять
через точки замкненої кривої. Ця крива
не повинна співпадати з якою-небудь
векторною лінією.
4)Векторне
поле – диференціальні характеристики(div
i
rot).
Озн:
частина
простору або весь простір, в кожній
точці якого визначений вектор
,
називається полем цього вектора, коротше
– векторним полем. Наприклад, а) у
просторі навколо Землі існує стаціонарне
гравітаційне векторне поле, на матеріальну
точку М, що знаходиться в цьому просторі
діє сила тяжіння
,
яка практично не залежить від часу, б)
навколо тіла, що має електричний заряд
маємо векторне поле напруги, яка проявляє
себе по відношенню до зарядженої
частинки, внесеної в це поле, в) нехай
в деяку просторову область Ω протікає
рідина зі швидкістю
,
тоді маємо гідродинамічне стаціонарне
поле швидкостей
рідини, що протікає.Диференціальні
характеристики. 1)
дивергенція (розходження) векторного
поля називається скалярна функція:
 – формальне означення. Інваріантне
означення:
– формальне означення. Інваріантне
означення:
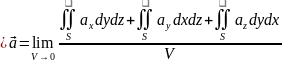 .
V
– об’єм,
обмежений поверхнею S.
За допомогою оператора Гамільтона
дивергенція записується:
.
V
– об’єм,
обмежений поверхнею S.
За допомогою оператора Гамільтона
дивергенція записується:
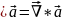 .
Дивергенція характеризує потужність
джерела або стоку поля швидкостей
рідини. Якщо
.
Дивергенція характеризує потужність
джерела або стоку поля швидкостей
рідини. Якщо
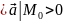 ,
то в точці
,
то в точці
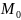 знаходиться джерело, а якщо
знаходиться джерело, а якщо
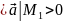 ,
то в точці
,
то в точці
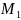 -
стік. 2) другою важливою характеристикою
є ротор. Ротором (вихором) векторного
поля
-
стік. 2) другою важливою характеристикою
є ротор. Ротором (вихором) векторного
поля
 Називається вектор, що задовольняє
рівності:
Називається вектор, що задовольняє
рівності:
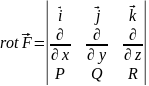 .
Цей символічний детермінант є векторний
добуток оператора Гамільтона і даного
вектора
.
.
Цей символічний детермінант є векторний
добуток оператора Гамільтона і даного
вектора
.
 - це формальне означення ротора,
інваріантне означення таке:
- це формальне означення ротора,
інваріантне означення таке:
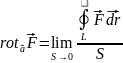 .
Ротор – вектор, проекція якого на
будь-який напрям нормалі
дорівнює границі відношення циркуляції
вектора
вздовж замкненого контура L
до площі нескінченно малої S,
яка містить точку М і перпендикулярна
.
З фізичної точки зору ротор характеризує
обертальну складову поля швидкостей
потока рідини. Якщо
є градієнт деякої скалярної функції
U,
то поле називається потенціальним.
.
Ротор – вектор, проекція якого на
будь-який напрям нормалі
дорівнює границі відношення циркуляції
вектора
вздовж замкненого контура L
до площі нескінченно малої S,
яка містить точку М і перпендикулярна
.
З фізичної точки зору ротор характеризує
обертальну складову поля швидкостей
потока рідини. Якщо
є градієнт деякої скалярної функції
U,
то поле називається потенціальним.
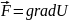 ,
величина
U
називається потенціалом поля.
,
величина
U
називається потенціалом поля.
5)Інтегральні
характеристики векторного поля –
робота, циркуляція, теор Стокса, формула
Гаусса-Остроградського.
Робота векторного поля(циркуляція).
Роботою векторного поля
вздовж лінії L
називається
величина криволінійного інтегралу
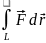 або
.
Якщо L
–
плоска, то
.
Якщо контур замкнений, то робота
векторного поля називається циркуляцією
вектора
вздовж цього замкненого контура.
Теорема:
циркуляція
потенціального вектора
вздовж замкненого контура дорівнює
нулю. Доведення:
або
.
Якщо L
–
плоска, то
.
Якщо контур замкнений, то робота
векторного поля називається циркуляцією
вектора
вздовж цього замкненого контура.
Теорема:
циркуляція
потенціального вектора
вздовж замкненого контура дорівнює
нулю. Доведення:
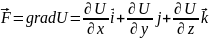 ,
тому
,
тому
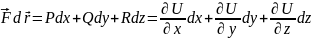 ;
;
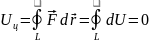 .
Інтеграл від повного диференціалу
дорівнює різниці значень функції U(xyz)
у кінцевій та початковій точках
інтегрування, а так як контур замкнений,
то ці точки співпадають, отже циркуляція
дорівнює нулю.
Теорема Стокса:
циркуляція
вздовж будь-якого замкненого контура
L
дорівнює потоку ротора через поверхню
S,
обмежену цим контуром. Це перша
інтегральна характеристика векторного
поля.
.
Інтеграл від повного диференціалу
дорівнює різниці значень функції U(xyz)
у кінцевій та початковій точках
інтегрування, а так як контур замкнений,
то ці точки співпадають, отже циркуляція
дорівнює нулю.
Теорема Стокса:
циркуляція
вздовж будь-якого замкненого контура
L
дорівнює потоку ротора через поверхню
S,
обмежену цим контуром. Це перша
інтегральна характеристика векторного
поля.
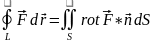 .Теорема
Гаусса-Остроградського:
ця
формула є аналог формули Стокса для
випадку замкненої поверхні. Вона зв’язує
потрійний інтеграл по просторовій
області V
з поверхневим інтегралом по зовнішній
стороні поверхні S,
що обмежує цю область. Формула має
вигляд:
.Теорема
Гаусса-Остроградського:
ця
формула є аналог формули Стокса для
випадку замкненої поверхні. Вона зв’язує
потрійний інтеграл по просторовій
області V
з поверхневим інтегралом по зовнішній
стороні поверхні S,
що обмежує цю область. Формула має
вигляд:
 ,
у векторній формі:
,
у векторній формі:
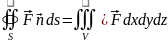 .
Теорема: потік
через замкнену поверхню S
у напрямі нормалі
до S
дорівнює потрійному інтегралу від
дивергенції цього вектора по області
V,
обмеженій поверхнею S.
Фіз. Смисл – потрійний інтеграл –
кількість рідини, що знаходиться в
об’ємі V,
за рахунок джерел з потужністю div
.
Ця кількість рідини дорівнює потоку
через поверхню S.
Формула ГО – це друга інтегральна
характеристика поля
.
.
Теорема: потік
через замкнену поверхню S
у напрямі нормалі
до S
дорівнює потрійному інтегралу від
дивергенції цього вектора по області
V,
обмеженій поверхнею S.
Фіз. Смисл – потрійний інтеграл –
кількість рідини, що знаходиться в
об’ємі V,
за рахунок джерел з потужністю div
.
Ця кількість рідини дорівнює потоку
через поверхню S.
Формула ГО – це друга інтегральна
характеристика поля
.