
- •Рисуночек(pict002)
- •7)Задача про роботу силового поля. Робота силового поля обчислюється двома шляхами: 1)в основу покладена властивість адитивності 2)основою даного розв’язку є формула Гріна: , де ;
- •4)Теор про середнє значення функції для потрійного інтегралу. Якщо функція f(X,y,z) – неперервна в замкнутій області , то існує точка в якій
- •9)Потрійні інтеграли у сферичних координатах. З маємо Отже, Обчислюємо якобіан переходу
- •10)Застосування потрійних інтегралів у геометрії та механіці. 1)Обчислення об’єму тіла.Якщо тіло однорідне і густина то об’єм дорівнює :
- •2)Координати центра мас тіла:
- •3)Момент інерції тіла відносно координатних осей:
- •2) Комплексні числа в тригонометричній та показниковій формах.
- •6)Основні властивості інтеграла від фкз, теорема Коші. Вони випливають з означення цього інтеграла:
- •Довжина .
- •1) Властивість лінійності перетворення Лапласа. Зображення функцій . T.Якщо , ,а і дійсні сталі то, ;і взагалі
- •7) Теор про інтегрування оригіналу.
1) Властивість лінійності перетворення Лапласа. Зображення функцій . T.Якщо , ,а і дійсні сталі то, ;і взагалі
Дов.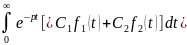 =
=
Скористаемося властивістю лінійності інтеграла

Так як властивість лінійності має місце для «n» властивість лінійності мае місце для доданків то одержемо загальне співвідношення.

 ;
;
 ;
;
2)Перетворення
Лапласа. Оригінал та зображення. Теорема
про подібність.
Т.Нехай
 оригінал
причому
диференційована при
оригінал
причому
диференційована при
 і
і
 також оригінал. Якщо
також оригінал. Якщо
 то:
то: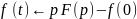 ЯКЩО
ЯКЩО
 оригінали то
оригінали то
 .Дов.
Розглянемо
інтеграл Лапласа для похідної
.Дов.
Розглянемо
інтеграл Лапласа для похідної
 U=
U=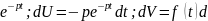 t
;
t
;
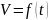 ;
=
;
= Формула
для зображення похідної n-го
порядку:
.;
Формула
для зображення похідної n-го
порядку:
.;
 ;
;
 або
або
 ;
Є
і інші позначення відносності
;
Є
і інші позначення відносності
 .
Перехід від функції
за формулою (1) називається перетворенням
Лапласа.Для збіжності невласного
інтеграла у формулі (1):а)
неперервна на всій осі
за винятком хіба що скінченного числа
точок розриву 1 роду на кожному інтервалі
скінченної довжини.б)
.
Перехід від функції
за формулою (1) називається перетворенням
Лапласа.Для збіжності невласного
інтеграла у формулі (1):а)
неперервна на всій осі
за винятком хіба що скінченного числа
точок розриву 1 роду на кожному інтервалі
скінченної довжини.б)
 ; М і
; М і
 -
деякі сталі;
-
деякі сталі;
 ;
;
 ;
;
 ;
Вважають
;
Вважають
 ;Функція
;Функція
 яка задовольняє вище згаданим трьом
умовам називається оригіналом. Відповідно
функція
яка задовольняє вище згаданим трьом
умовам називається оригіналом. Відповідно
функція
 яка визначається формулою (1) називається
зображенням
.Теорема
єдності (без дов)
ЯКЩО ДВІ НЕПЕРЕРВНІ ФУНКЦІЇ
І
яка визначається формулою (1) називається
зображенням
.Теорема
єдності (без дов)
ЯКЩО ДВІ НЕПЕРЕРВНІ ФУНКЦІЇ
І
 мають одне і те саме зображення
то
ці функції тотожно рівні.Теорема
про подібність
і
мають одне і те саме зображення
то
ці функції тотожно рівні.Теорема
про подібність
і
 ,то
,то
 ;
Дов.
;
Дов.
 ;
;
 зробимо заміну змінної інтегрування
[
зробимо заміну змінної інтегрування
[ ;
;
 ;]
;]

3)Перетворення
Лапласа. Оригінал та зображення. Теорема
про зсув.
Т.Нехай
оригінал
причому
диференційована при
і
також оригінал. Якщо
то:
ЯКЩО
оригінали то
.Дов.
Розглянемо
інтеграл Лапласа для похідної
U=
t
;
;
=
Формула
для зображення похідної n-го
порядку:
.;
;
або
;
Є
і інші позначення відносності
.
Перехід від функції
за формулою (1) називається перетворенням
Лапласа.Для збіжності невласного
інтеграла у формулі (1):а)
неперервна на всій осі
за винятком хіба що скінченного числа
точок розриву 1 роду на кожному інтервалі
скінченної довжини.б)
; М і
-
деякі сталі;
;
;
;
Вважають
;Функція
яка задовольняє вище згаданим трьом
умовам називається оригіналом. Відповідно
функція
яка визначається формулою (1) називається
зображенням
.Теорема
єдності (без дов)
ЯКЩО ДВІ НЕПЕРЕРВНІ ФУНКЦІЇ
І
мають одне і те саме зображення
то
ці функції тотожно рівні.
Теорема
про зсув:Якщо
 то
то
 ;Дов.
;Дов.
 ;
;
4)Перетворення
Лапласа. Оригінал та зображення. Теорема
про запізнювання.
Т.Нехай
оригінал
причому
диференційована при
і
також оригінал. Якщо
то:
ЯКЩО
оригінали то
.Дов.
Розглянемо
інтеграл Лапласа для похідної
U=
t
;
;
=
Формула
для зображення похідної n-го
порядку:
.;
;
або
;
Є
і інші позначення відносності
.
Перехід від функції
за формулою (1) називається перетворенням
Лапласа.Для збіжності невласного
інтеграла у формулі (1):а)
неперервна на всій осі
за винятком хіба що скінченного числа
точок розриву 1 роду на кожному інтервалі
скінченної довжини.б)
; М і
-
деякі сталі;
;
;
;
Вважають
;Функція
яка задовольняє вище згаданим трьом
умовам називається оригіналом. Відповідно
функція
яка визначається формулою (1) називається
зображенням
.Теорема
єдності (без дов)
ЯКЩО ДВІ НЕПЕРЕРВНІ ФУНКЦІЇ
І
мають одне і те саме зображення
то
ці функції тотожно рівні.
Теорема про запізнюванняЯкщо
і
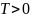 то
то
 ;Дов.
;Дов.
 ;
; [
[ ;
;
 ;
;
 ]
]
 [Скористаємося
адитивності невласного інтеграла]
[Скористаємося
адитивності невласного інтеграла] [
[ коли
коли
 отже
1 інтеграл = 0]
отже
1 інтеграл = 0] .
.
5)Теор
про диференціювання оригінала
Нехай f(t)
– оригінал, пичому f(t)
диференційована при
і f’(t)
також оригінал. Тоді якщо
 ,
то
,
то
 ,
якщо крім того
,
якщо крім того
 - є оригіналом, то
- є оригіналом, то
 .Дов.
розглянемо інтеграл Лапласа для похідної
f’(t):
.Дов.
розглянемо інтеграл Лапласа для похідної
f’(t):
 =[про
інтегруємо частинами
=[про
інтегруємо частинами
 ]=
]= .
Після ‘n’
кратного застосування цього способу
одержимо формулу для зображення похідної
‘n’ го
порядку.
.
Після ‘n’
кратного застосування цього способу
одержимо формулу для зображення похідної
‘n’ го
порядку.
6)Теор
про диференціювання зображення
Нехай
 ,
то з теорії ФКЗ відомо, що f(p)
є аналітична функція півплощини
,
тобто має похідні всіх порядків. Тоді
похідна ‘n’
го порядку
,
то з теорії ФКЗ відомо, що f(p)
є аналітична функція півплощини
,
тобто має похідні всіх порядків. Тоді
похідна ‘n’
го порядку
 є зображення функції
є зображення функції
 .
.
 .Дов.
.Дов.
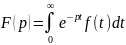 ;
за теоремою про диференціювання
невласного інтегралу за параметром
маємо:
;
за теоремою про диференціювання
невласного інтегралу за параметром
маємо:
 .
Диференціюючи ‘n’
разів за параметрои р, одержуємо
відповідне спріввідношення.
.
Диференціюючи ‘n’
разів за параметрои р, одержуємо
відповідне спріввідношення.
