- •Scan Pirat
- •Глава IV. Перемещение и сжатие газов (компрессорные машины)
- •Общие сведения . . .
- •Сравнение и области применения компрессорных машин различных
- •Глава V. Разделение неоднородных систем 176
- •Общие сведения 186
- •Общие сведения . 227
- •Глава VI. Перемешивание в жидких средах 246
- •Общие сведения 246
- •Глава VII. Основы теплопередачи в химической аппаратуре 260
- •Общие сведения 260
- •Глава VIII. Нагревание, охлаждение и конденсация 310
- •Общие сведения . 310
- •Нагревание газообразными высокотемпературными теплоносителями
- •Общие сведения . 347
- •Общие сведения 382
- •Общие сведения 434
- •Глава XV. Сушка . . .Ч 583
- •Глава XVI. Кристаллизация 632
- •Глава XVII. Искусственное охлаждение 646
- •Циклы, основанные на сочетании дросселирования и расширения газа
- •Глава XVIII. Измельчение твердых материалов 679
- •Общие сведения 679
- •Крупное дробление 684
- •Тонкое измельчение n 693
- •Глава XIX. Классификация и сортировка материалов 703
- •Глава XX. Смешение твердых материалов 711
- •2. Возникновение и развитие науки о процессах и аппаратах
- •Возникновение и развитие науки о процессах и аппаратах
- •3. Классификация основных процессов
- •4. Общие принципы анализа и расчета процессов и аппаратов
- •Общие принципы анализа и расчета процессов и аппаратов
- •Основные определения
- •Некоторые физические свойства жидкостей
- •2. Некоторые физические свойства жидкостей
- •Некоторые физические свойства жидкостей
- •Некоторые физические свойства жидкостей
- •Дифференциальные уравнения равновесия Эйлера
- •Основное уравнение гидростатики
- •Основное уравнение гидростатики
- •Основные характеристики движения жидкостей
- •Основные характеристики движения жидкостей
- •6. Основные характеристики движения жидкостей
- •6. Основные характеристики движения жидкостей
- •6. Основные характеристики движения жидкостей
- •6. Основные характеристики движения жидкостей
- •48 Гл. II. Основы гидравлики. Общие вопросы прикладной гидравлика
- •Уравнение неразрывности (сплошности) потока
- •8. Дифференциальные уравнения движения Эйлера
- •9. Дифференциальные уравнения движения Навье—Стокса
- •9., Дифференциальные уравнения движения Навье—Стокса
- •10. Уравнение Бернулли
- •10. Уравнение Бернулли
- •Некоторые практические приложения уравнения Бернулли
- •11. Некоторые практические-приложения уравнения Бернулли
- •12« Основы теории подобия и анализа размерностей.
- •12. Основы теории подобая а анализа размерностей. Принципы моделирования 71
- •12. Основы теории подобия и анализа размерностей. Принципы моделирования п
- •Гидродинамическое подобие
- •13. Гидродинамическое подобие
- •13. Гидродинамическое подобия
- •13. Гидродинамическое подобие
- •Гидравлические сопротивления в трубопроводах
- •14. Гидравлические сопротивления в трубопроводах
- •14. Гидравлические сопротивления в трубопроводах
- •Течение неньютоновских жидкостей
- •Закономерности движения неньютоновских жидкостей имеют ряд особенностей. - Для обычных, или ньютоновских, жидкостей зависимость между напряжением сдвига т
- •Неньютоновские жидкости можно разделить на три большие группы. К первой группе относятся так называемые вязкие, или стационарные, не- ньютоновские жидкости. Для этих
- •Времени. По виду данной функции (кривой тече- нии) различают следующие разновидности жид- костей этой группы.
- •Называемый пластическо
- •Зависимость (11,105) изображается на рис. 11-26 линией 2
- •15. Течение неньютоновских жидкостей
- •Ростях сдвига; в результате величины и х становятся пропорциональными друг другу
- •Расчет диаметра трубопроводов
- •17. Движение тел в жидкостях
- •Движение тел в жидкостях
- •17. Движение тел в жидкостях
- •18. Движение жидкостей через неподвижные зернистые и пористые слои 101
- •Движение жидкостей через неподвижные зернистые и пористые слои
- •18. Движение жидкостей через неподвижные зернистые и пористые слои 103
- •Для полидисперсных зернистых слоев расчетный диаметр (1 вычисляют из соотношения
- •18. Движение жидкостей через неподвижные зернистые и пористые слои 105
- •19. Гидродинамика кипящих (псевдоожиженных) зернистых слоев 107
- •19. Гидродинамика кипящих (псевдоожиженных) зернистых слоев 109
- •20. Элементы гидродинамики двухфазных потоков
- •Элементы гидродинамики двухфазных потоков
- •20. Элементы гидродинамики двухфазных потоков
- •20. Элементы гидродинамики двухфазных потоков
- •Структура потоков и распределение времени пребывания жидкости в аппаратах
- •Глава III
- •Перемещение жидкостей (насосы)
- •Общие сведения
- •Основные параметры насосов
- •3. Напор насоса. Высота всасывания
- •Центробежные насосы
- •4. Центробежные насосы
- •4. Центробежные насосы
- •4. Центробежные насосы
- •4. Центробежные насосы
- •Поршневые насосы
- •5. Поршневые насосы
- •5. Поршневые насосы
- •Специальные типы поршневых и центробежных насосов
- •Насосы других типов
- •7. Насосы других типов
- •7. Насосы других типов
- •Сравнение и области применения насосов различных типов
- •8. Сравнение и области применения насосов различных типов
- •Глава IV
- •Перемещение и сжатие газов (компрессорные машины)
- •Общие сведения
- •2. Термодинамические основы процесса сжатия газов
- •2.. Термодинамические основы процесса сжатия газов
- •2. Термодинамические основы процесса сжатия газов
- •3. Поршневые компрессоры
- •Поршневые компрессоры
- •3. Поршневые компрессоры
- •3. Поршневые компрессоры
- •3. Поршневые компрессоры
- •4. Ротационные компрессоры и газодувки
- •Ротационные компрессоры и газодувки
- •6. Осевые вентиляторы и компрессоры
- •Осевые вентиляторы и компрессоры
- •Винтовые компрессоры
- •Вакуум-насосы
- •8. Вакуум-насосы
- •Глава V
- •1. Неоднородные системы и методы их разделения
- •Материальный баланс процесса разделения
- •Скорость стесненного осаждения (отстаивания)
- •3. Скорость стесненного осаждения (отстаивания)
- •4. Коагуляция частиц дисперсной фазы
- •Коагуляция частиц дисперсной фазы
- •Отстойники
- •5. Отстойники
- •5. Отстойники
- •Общие сведения
- •6. Общие сведения
- •6. Общие сведения
- •Уравнения фильтрования
- •8. Фильтровальные перегородки
- •Фильтровальные перегородки
- •Устройство фильтров
- •9. Устройство фильтров
- •9. Устройство фильтре*
- •9. Устройство фильтров
- •9. Устройство фильтров
- •9. Устройство фильтров
- •9. Устройство фильтров
- •10. Расчет фильтров
- •9. Устройство фильтров
- •Основные положения
- •12. Центробежная сила и фактор разделения
- •Центробежная сила и фактор разделения
- •Процессы в отстойных центрифугах
- •Процессы в фильтрующих центрифугах
- •Устройство центрифуг
- •16. Расчет центрифуг
- •16. Расчет центрифуг
- •17. Общие сведения
- •17. Общие сведения
- •18. Гравитационная очистка газов
- •2 Камера; 2 — горизонтальные перегородки (полки)! 3 — отражательная перегородка; 4 *- дверцы.
- •Очистка газов под действием инерционных и центробежных сил
- •20. Очистка газов фильтрованием
- •Очистка газов фильтрованием
- •Мокрая очистка газов
- •21. Мокрая очистка газов
- •Электрическая очистка газов
- •22. Электрическая очистка газов
- •22. Электрическая очистка газов
- •23. Коагуляция и укрупнение частиц, отделяемых при газоочистке
- •Коагуляция и укрупнение частиц, отделяемых при газоочистке
- •24. Сравнительные характеристики и выбор газоочистительной аппаратуры 245
- •Глава VI
- •2. Механическое перемешивание
- •2. Механическое перемешивание
- •2. Механическое перемешивание
- •3. Механические перемешивающие устройства
- •3. Механические перемешивающие устройства
- •Пневматическое перемешивание
- •5. Перемешивание в трубопроводах
- •Перемешивание в трубопроводах
- •6. Перемешивание с помощью сопел и насосов
- •2. Тепловые балансы
- •Тепловые балансы
- •Основное уравнение теплопередачи
- •4. Температурное поле и температурный градиент
- •Температурное поле и температурный градиент
- •Передача тепла теплопроводностью
- •5. Передача тепла теплопроводностью
- •5. Передача тепла теплопроводностью
- •Тепловое излучение
- •6. Тепловое излучение
- •6. Тепловое излучение
- •7. Передача тепла конвекцией (конвективный теплообмен)
- •Передача тепла конвекцией (конвективный теплообмен)
- •7. Передача тепла конвекцией (конвективный теплообмен) 277
- •7. Передача тепла конвекцией (конвективный теплообмен) 279
- •8. Опытные данные по теплоотдаче
- •Опытные данные по теплоотдаче
- •8. Опытные данные по теплоотдаче
- •8. Опытные данные по теплоотдаче
- •8. Опытные данные по теплоотдаче
- •8. Опытные данные по теплоотдаче
- •10. Сложная теплоотдача
- •Численные значения коэффициентов теплоотдачи
- •Сложная теплоотдача
- •Теплопередача
- •11. Теплопередача
- •11. Теплопередача
- •11. Теплопередача
- •12., Нестационарный теплообмен
- •12. Нестационарный теплообмен
- •Дгср _ ——-f - j_t -
- •12. Нестационарный теплообмен
- •Глава VIII нагревание, охлаждение и конденсация
- •Общие сведения
- •Нагревание водяным паром
- •Центробежный насос.
- •4. Нагревание топочными газами
- •Нагревание горячей водой
- •Нагревание топочными газами
- •1 Сопло горелки; 2 —- огнеупорная пористая панель; 3 — радиантная часть (змеевик); 4 — конвективная часть (змеевик); 5 — перегреватель; 6 и- дымовая труба.
- •Нагревание высокотемпературными теплоносителями
- •I печь со змеевиком; 2 — теплоиспользующнй аппарат; 3 подъемный трубопровод; 4 — опускной трубопровод; 5 — циркуляционный насос.
- •Нагревание электрическим током
- •Охлаждение до обыкновенных температур
- •Охлаждение до низких температур
- •Конденсация паров
- •Трубчатые теплообменники
- •Змеевиковые теплообменники
- •Пластинчатые теплообменники
- •Оребренные теплообменники
- •16. Теплообменные устройства реакционных аппаратов
- •Конденсаторы смешения
- •Расчет теплообменных аппаратов
- •Расчет конденсаторов паров
- •Глава IX
- •Общие сведения
- •Однокорпусные выпарные установки
- •2. Однокорпусные выпарные установки
- •3. Многокорпусные выпарные установки
- •Многокорпусные выпарные установки
- •3. Многокорпусные выпарные установки
- •Устройство выпарных аппаратов
- •Расчет многокорпусных выпарных аппаратов
- •Общие сведения
- •1. Общие сведения
- •Равновесие при массопередаче
- •Скорость массопередачи
- •3. Скорость массопередачи
- •Движущая сила процессов массопередачи
- •Массопередача с твердой фазой
- •6. Массопередача с твердой фазой
- •Глава XI
- •Равновесие при абсорбции
- •Материальный и тепловой балансы процесса
- •Скорость процесса
- •Устройство абсорбционных аппаратов
- •— Щели.
- •Расчет абсорберов
- •7. Десорбция
- •8. Схемы абсорбционных установок
- •Глава XII
- •Характеристики двухфазных систем жидкость—пар
- •4. Ректификация
- •4. Ректификация
- •Специальные виды перегонки
- •Глава XIII
- •Общие сведения
- •2. Равновесие в системах жидкость—жидкость
- •2. Равновесие в системах жидкость—жидкость
- •2. Равновесие в системах жидкость—жидкость
- •2. Равновесие в системах жидкость—жидкость
- •3. Методы экстракции
- •3. Методы экстракции
- •3. Методы экстракции
- •1/ 2, 8, .... П — ступени.
- •3. Методы экстракции
- •3. Методы экстракции
- •3. Методы экстракции
- •4. Устройство экстракционных аппаратов
- •Ступенчатые экстракторы
- •4. Устройство экстракционных аппаратов
- •4. Устройство экстракционных аппаратов
- •1Л. XIII. Экстракция
- •4. Устройство экстракционных аппаратов
- •5. Расчет экстракционных аппаратов
- •5. Расчет экстракционных аппаратов
- •7. Равновесие и скорость процессов экстракции и растворения
- •Рис, хііі-27. Схема извлечения растворенного вещества из пористого тела и профиль концентраций.
- •Способы экстракции и растворения
- •8. Способы экстракции и растворения
- •Рнс. Хііі-29. Схема противоточной промывки осадка (шлама) на барабанных вакуум-фильтрах:
- •Устройство экстракционных аппаратов
- •9. Устройство экстракционных аппаратов
- •9. Устройство экстракционных аппаратов
- •Расчет экстракционных аппаратов
- •Глава XIV
- •Общие сведения
- •2. Характеристики адсорбентов и их виды
- •Равновесий при адсорбции
- •3. Равновесие при адсорбции
- •Скорость адсорбции
- •4. Скорость адсорбции
- •4. Скорость адсорбции
- •Десорбция
- •5. Десорбция
- •6. Устройство адсорберов и схемы адсорбционных установок
- •6. Устройство адсорберов и схемы адсорбционных установок
- •Расчет адсорберов
- •7. Расчет адсорберов
- •Ионообменные процессы
- •Глава XV
- •Основные параметры влажного газа
- •Равновесие при сушке
- •Материальный и тепловой балансы сушки
- •Определение расходов воздуха и тепла на сушку
- •Варианты процесса сушки
- •Скорость сушки
- •8. Скорость сушки
- •Dwc cftuiP
- •Устройство суЬшлок
- •Конвективные сушилки с неподвижным или движущимся плотным слоем материала
- •Конвективные сушилки с перемешиванием слоя материала
- •Конвективные сушилки со взвешенным слоем материала
- •1 Верхняя камера; 2 — нижняя камера; 3 — раз» рыхлитель.
- •I камера сушилки; 2 — полые плиты.
- •Глава XVI
- •1, Общие сведения
- •Равновесие при кристаллизации
- •Влияние условий кристаллизации на свойства кристаллов
- •Способы кристаллизации
- •Устройство кристаллизаторов
- •I __ труба аппарата; 2 — термоизоляционный кожух; 3 — вентилятор; 4 — труба
- •7. Расчеты кристаллизаторов Материальный баланс кристаллизации
- •Глава XVII искусственное охлаждение
- •Общие сведения
- •Термодинамические основы получения холода
- •Другие методы получения низких температур
- •Компрессионные паровые холодильные машины
- •Абсорбционные холодильные машины
- •Пароводяные эжекторные холодильные машины
- •Циклы с дросселированием газа
- •Циклы с тепловым насосом
- •Сравнение основных циклов глубокого охлаждения
- •Методы разделения газов
- •Механические процессы
- •Глава XVIII измельчение твердых материалов
- •Общие сведения
- •Физико-механические основы измельчения.
- •Щековые дробилки
- •Конусные дробилки
- •Валковые дробилки
- •Ударно-центробежные дробилки
- •Барабанные мельницы
- •Кольцевые мельницы
- •8 Сепаратор Материал
- •Мельницы для сверхтонкого измельчения
- •Глава XIX
- •Классификация и сортировка материалов
- •Грохочение
- •Гидравлическая классификация и воздушная сепарация
- •Глава XX
- •328 Расчет 343
- •Основные процессы и аппараты химической технологии
60
Гл.
II. Основы гидравлики. Общие вопросы
прикладной гидравлики
Выражение
(11,44) или (11,44а) представляет собой
уравнение
неразры внести (сплошности) потока в
его интегральной форме
для установившегося движения. Это
уравнение называется также уравнением
постоянства расхода.
Согласно
уравнению постоянства расхода, при
установившемся движении жидкости,
полностью заполняющей трубопровод,
через каждое его поперечное сечение
проходит в единицу времени одна и та
же масса жидкости.
в
различных поперечных сечениях
трубопровода обратно пропорциональны
площадям этих сечений.
Согласно
уравнению (11,44), массовый расход жидкости
через начальное сечение трубопровода
равен ее расходу через конечное сечение
трубопровода. Таким образом, уравнение
постоянства расхода является частным
случаем закона сохранения массы
и выражает материальный
баланс потока.
В
некоторых случаях, например при вскипании
жидкости вследствие резкого понижения
давления, образуется пар, что может
привести к разрыву потока. В таких
условиях, наблюдаемых иногда при работе
насосов, уравнение неразрывности потока
не выполняется.
Рассмотрим
установившийся поток идеальной жидкости.
Как уже говорилось, она не обладает
вязкостью, т. е. движется без трения.
Как
и при выводе дифференциальных уравнений
равновесия Эйлера, выделим в потоке
элементарный параллелепипед .объемом
йУ
= йхйуйг,
ориентированный
относительно осей координат (см. рис.
11-2).
Выше
было показано (см. стр, 31), что проекции
на оси координат сил тяжести и давления,
действующих на параллелепипед,
составляют: для оси х
Согласно
основному принципу динамики, сумма
проекций сил, действующих на движущийся
элементарный объем жидкости, равна
произведению массы жидкости на ее
ускорение.
Масса
жидкости в объеме параллелепипеда
Для
капельных жидкостей рх = = р2
= р3 = р = const, и
уравнение (11,44) принимает вид
Следовательно
ffiijS-,
= ai2S2
= wsSs
= const (11,45a)
или
Рис.
II-13. К выводу уравнения
постоянства расхода.
Qi
— Qi
—
Qs
где
Q = o)S — объемный
расход жидкости, мУсек.
Из
уравнения (11,45а) следует.
что
скорости
капельной жидкости
для
оси у
для
оси г
(pg-f-
dxdydz
dm
=
pdxdydz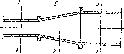

8. Дифференциальные уравнения движения Эйлера
|
дХ2)х |
|
+ • |
дшх |
Щ + |
да)х |
йх |
дх |
|
ду |
дг |
||
скюу _ |
дту |
шх |
+ |
диіу |
™у + |
до)у |
йх |
дх |
ду |
дг |
|||
1 1 |
дт>2 |
|
+ ■ |
Звуг |
|
діа2 |
йх |
дх |
іюх |
ду |
ту г |
дг |
шг
Юг
(II
>47)
Система
уравнений (11,46) с учетом выражений
(11,47) представляет собой дифференциальные
уравнения движения идеальной жидкости
Эйлера для установившегося потока.
При
неустановившемся движении скорость
жидкости изменяется не только при
перемещении частицы потока из одной
точки пространства в другую, но и с
течением времени в каждой точке. Поэтому,
в соответствии с уравнением (11,28),
составляющие ускорения в уравнении
(11,46), выражаемые субстанциональными
производными для неустановившихся
условий, имеют вид:
йтх
дшх
йх
йпВу
(їх
иО)г
йх
дх
дпоу
дх
дшг
дх
дмх
дх
ды)у
дх
діщг
дх
+
ш.
ди>х
ду
дщ
ду
да»г
ду
■а>д
+
дг
дг
дхазг
дг
(11,47а)
Б2 Гл.
II. Основы гидравлики. Общие вопросы
прикладной гидравлики
Система
уравнений (11,46) с учетом выражений
(11,47а) представляет
собой дифференциальные
уравнения движения
идеальной жидкости
Эйлера для неустановив-
шегвся
потока.
Как
показано ниже (стр. 54 сл.), интегралом
уравнений движения
Эйлера
для-установившегося потока является
уравнение Бернулли, ши-
роко
используемое для решения многих
технических задач.
При
движении реальной (вязкой) жидкости в
потоке жидкости помимо
сил давления
и тяжести действуют также силы трения.
Действие
сил трения Т
на выделенный в потоке вязкой жидкости
эле-
ментарный параллелепипед (рис.
II-14) проявляется в возникновении на его
поверхности
касательных напряжений т. Рас-
смотрим
первоначально относительно про-
стой
случай одномерного
плоского
потока капельной
жидкости в напра-
влении оси х,
когда проекция скорости хюх
зависит
только от расстояния г
до горизон-
тальной плоскости отсчета.
В
этих условиях касательные напряже-
ния
возникают лишь на поверхностях йР
верхней
и нижней граней элементарного
параллелепипеда,
причем <1Р
= йхйу.
Если
касательное напряжение на
нижней грани
параллелепипеда равно
т, то на верхней оно
составляет
(т + йг^
.
Производная -Щ-
выражает
изменение касательного напря-
жения
вдоль оси 2
в точках, лежащих на нижней грани
параллелепи-
педа, а йг
представляет собой изменение этого
напряжения вдоль
всей
длины йг
ребра параллелепипеда.
Указанные
на рис. II-14 стрелками направления сил
трения, прило-' женных к параллелепипеду
на его нижней и верхней гранях,
обусловлены, например, тем, что более
медленные вышележащие слои жидкости
затормаживают слой, в котором
находится параллелепипед, а более
быстрые нижележащие слои «разгоняют»
его (вспомним, что на стр. 26 мы условились
проводить нормаль к поверхностям
соприкосновения перемещающихся
относительно друг друга слоев в
направлении уменьшения их скорости).
Тогда
проекция равнодействующей сил трения
на ось х
гйхйу
— (т + йг
) йхйу
— йхйуйг
Подставив
в это выражение значение касательного
напряжения т по уравнению (II, 12а) {т = —у,
где у
— вязкость жидкости], получим
д
\
дг / ...
д2сг>*
...
Р- ^ йхйуйг
= ц йхйуйг
В
более общем случае трехмерного потока
составляющая скорости ы>х
будет
изменяться не только в направлении г,
но и в направлениях всех трех осей
координат. Тогда проекция равнодействующей
сил трения на ось х
примет вид
Рис.
П-14. К выводу уравнений Навье—Стокса.
/
д*0)х дгхюх
\ . . .
**
\-~W-
+
~ду*~ +
-ЯГ) Лхйуй*9. Дифференциальные уравнения движения Навье—Стокса