94. Аппроксимации характеристик нелинейных элементов

Виды аппроксимаций:

1) Кусочно – линейная : а) в)

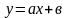
2) Аппроксимация укороченным степенным полиномом

а)

б)

3) Аппроксимация гиперболическим синусом:

4) Аппроксимация степенным полиномом:

5) Аппроксимация экспоненциальным полиномом:

И т.д. и т.п.

Для определение коэффициентов аппроксимации нелинейных элементов:

а )

б) ;

в) Аппроксимация гиперболическим синусом:

Когда , величиной можно пренебречь из – за ее малости. Тогда:

Вопрос №95 Последовательность расчета нелинейных электрических цепей постоянного тока аналитическими методами

1. Аппроксимируем характеристики НЭ

2. Составляем систему уравнений по методу уравнений Кирхгофа или узловых потенциалов

3. Подставляем в полученную систему уравнений аппроксимируемое выражения

4. Решаем полученную систему и находим токи и напряжения на нелинейных элементах

Достоинства:

Позволяет анализировать задачу в общем виде

Недостатки:

• Сложность

• Непригодность для расчета сложных электрических цепей

Пример:

1 ). I_н=аU_н² (1)

2). I₁-I₂-I_н=0

I₂R₂=U_н (2)

I₁R₁+U_н=Е

( 3)

( 4) 1,3,4 2

Решая полученное квадратное уравнение определяем напряжение на НЭ.

96. Расчет нелинейных электрических цепей постоянного тока методом итераций

Одним из численных методов расчета является метод итераций:

1). Задаемся произвольным значением тока I₁ и по ВАХ НЭ1 определяем U₁

2 ). По закону Ома I₂=U₁\R₂

3). I₃ определяем по 1-му закону Кирхгофа I₃=I₁+I₂

4). По ВАХ 3-го НЭ3 определяем U₃

5). Определяем расчетную ЭДС по 2-му закону Кирхгофа

E_расч=U₁+U₃+I₃R₄

6 ). Расчет ведем до тех пор, пока расчетная ЭДС не станет достаточно близка по значению к действительной.

Этого можно добиться 2-мя способами:

1-ый способ:

Задаваясь различными значениями тока I₁ определяем расчетные ЭДС и строим вспомогательную характеристику E(I₁).

Вопрос 97

Метод Ньютона – Рафсона.

Сущность метода заключается в том, что каждое следующее приближение равно предыдущему минус поправка, равная отношению функции предыдущего приближения к ее производной:

Для сходимости вычислительного процесса необходимо:

1) Функция должна быть дифференцируема.

2) Значение производной не должно быть слишком мало.

Пример расчета:

U₁=aIⁿ;(a=1;n=2)

U₂= sh( I);( =1; =1)

U₁+U₂=E

f(I)=I²+shI – E= I²+shI – 1

f’(I)=2I+chI

1. I₍₀₎=0; f(I₍₀₎)=0+sh0 – 1 = 1

f’(I₍₀₎)=0+1=1

I₍₁₎=I₍₀₎ - =0 + 1=1

2. I₍₁₎=1; f(I₍₀₎)=1²+sh1 – 1=1,17

f’(I)=2+ch1=3,54

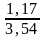I₍₂₎=I₍₁₎ - =1- =0,67

3) I₍₂₎=0,67; и т.д. до тех пор, пока величина I_(n) не начнет повторяться,

т.е. I_(k+1) – I_(k)=0.

Достоинства и недостатки численных методов:

Достоинства: позволяют рассчитывать сколь угодно сложные цепи с любой точностью.

Недостатки: не позволяют анализировать задачу в общем виде.