3.3. IMPROVEMENTS IN THE PERFORMANCE OF LEVEL-3 NVIDIA CUBLAS

Figure 3.6: Percentage of time devoted to data transfers for the matrix-matrix multiplication. The plots include the e ective bandwidth o ered by the PCI-Express bus using non-pinned memory and pinned memory (left and right, respectively).

3.3.Improvements in the performance of Level-3 NVIDIA CUBLAS

After analyzing the previous results, we conclude that the routine implementations in NVIDIA CUBLAS exhibit heterogeneous performances. This irregular behavior depends not only on the particular operation (compare the performance of di erent BLAS-3 routines in Figure 3.5), but also on each specific case of each routine (see the behavior of each case for the GEMM routine in NVIDIA CUBLAS on Figure 3.3).

This irregular behavior justifies one of the contributions of the work presented in this thesis. Low-level programming requires a deep knowledge of the underlying architectural details and adhoc programming languages. Very often, these details are closed to the scientific community; in other cases, even the hardware vendors are not able to fully exploit them for every implementation.

Developing a low-level approach from the initial stages of the library development is not always the correct choice. Several key decisions can have critical consequences on performance, and very frequently they are di cult to evaluate when programming at low level, driving to a loss of e ciency in the programming e ort.

In this section, we demonstrate how, by applying some high-level methodologies for the derivation and evaluation of dense linear algebra algorithms, it is possible to extract key insights that are crucial to deliver high-performance codes. Moreover, we also show that these codes are highly competitive from the performance perspective, attaining better performance results than those obtained with a low-level programming methodology.

Our implementations improve the performance of the NVIDIA CUBLAS routines by applying two main techniques. First, for each BLAS-3 routine we cast a major part of the operations in terms of the high performance GEMM routine. Second, we systematically derive a full set of blocked algorithmic variants and evaluate them to find out the optimal one for each combination of parameter values and routine. Other parameters, such as the block size, are also systematically studied for each algorithmic variant. The result is a full evaluation and a high-performance implementation of the main routines in the Level-3 BLAS. The attained results clearly improve those in NVIDIA CUBLAS for the tested routines.

53

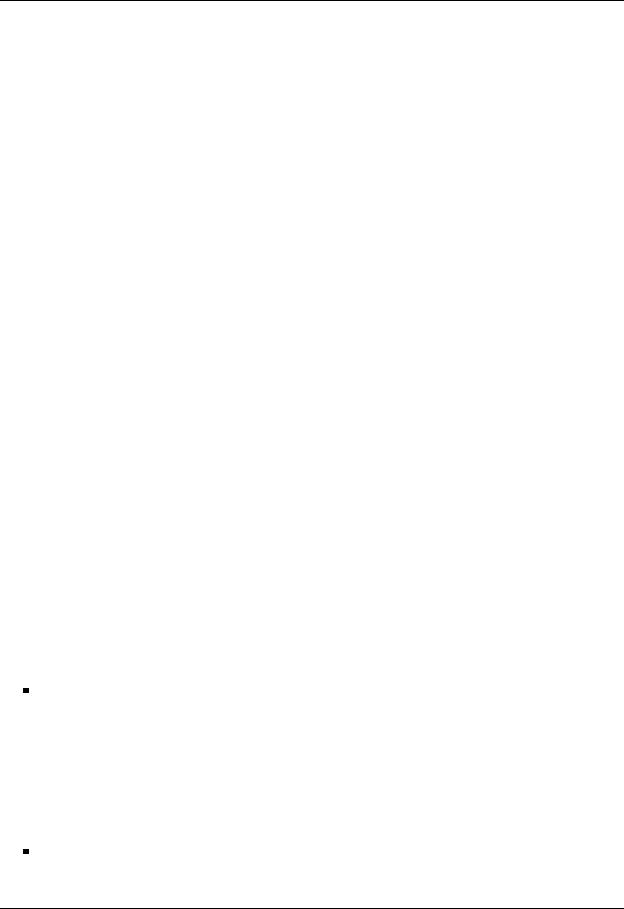
CHAPTER 3. BLAS ON SINGLE-GPU ARCHITECTURES

3.3.1. GEMM-based programming for the Level-3 BLAS

Improving the performance of the BLAS usually involves a deep knowledge of the internals of the target architecture, in this case the graphics architecture provided by NVIDIA, and a hard coding effort. This deep knowledge is often translated into a small set of complex and e cient codes adapted to the underlying architecture [142]. An illustrative example of this development complexity, as exposed in Section 3.2.1, is the NVIDIA CUBLAS implementation. While the GEMM implementation in NVIDIA CUBLAS delivers high performance, the rest of the Level-3 NVIDIA CUBLAS routines are sub-optimal, o ering worse e ciency, far from that attained for the general matrix-matrix multiplication. This performance analysis gives an idea of the necessary programming e ort in the development of tuned codes for the GPU.

However, there is a di erent way for developing high performance kernels for the BLAS. Following this alternative approach, the new implementations of the BLAS are based on a small set of tuned codes, or inner kernels, taking benefit from their high performance to boost the performance of the new codes. This approach has been successfully applied in other high performance BLAS implementations, such as GotoBLAS [72] for general-purpose processors, attaining remarkable speedups without a ecting the development e ort. As a novelty, we apply a similar technique for the development of a full set of optimized dense linear algebra routines for modern graphics processors.

Besides increasing performance, the main advantage of the usage of tuned inner kernels is programmability. With this approach, the low-level architectural details have already been exploited in the inner-kernel implementation, and in consequence the programmer does not have to deal with them in the new codes. In addition, any further optimizations of the inner kernel will automatically translate into an improvement in the performance of higher-level codes, without any additional development e ort.

Given the performance results observed in Section 3.2.1, in our case it will be convenient to use the GEMM implementation in NVIDIA CUBLAS as the building block for developing the rest of the tuned BLAS. In other words, the main goal is to derive algorithms for the BLAS-3 routines that reformulate a big part of its operations in terms of the high-performance GEMM implementation in

NVIDIA CUBLAS.

This technique was first applied for general-purpose architectures by K˚agstr¨om, Per Ling and Van Loan [88], but the GEMM-based concept can be ported to any architecture as long as there exists a tuned implementation of the general matrix-matrix multiplication routine, to build a complete and tuned BLAS-3 implementation.

Building a BLAS-3 based on this guidelines involves some remarkable advantages:

The GEMM routine is usually illustrative of the peak performance of the architecture, so manufacturers often devote big e orts to tune it, delivering near optimal implementations for their own architectures. Although the e ciency of the GEMM implementation in NVIDIA CUBLAS, is far from the theoretical peak of the architecture, this routine is considered to be a near-optimal implementation that exploits all the capabilities of the GPU for generalpurpose applications, and thus it is considered to reflect the practical peak performance of the architecture for this type of implementations [142]. Our GEMM-based implementations will inherit this high performance for each BLAS-3 routine.

With this approach, the optimizing e ort can be focused on just one routine (in this case, the matrix-matrix multiplication). The potential benefits of the optimization work will be immediately e ective for the rest of the routines. Similarly, with the advent of new architectures,

54

3.3. IMPROVEMENTS IN THE PERFORMANCE OF LEVEL-3 NVIDIA CUBLAS

or even with future modifications of the current ones, only one routine should be adapted to the new hardware in order to get a global boost in performance.

Although this is a high-level approach, the insights gained from the evaluation of new routines (for example, optimal block sizes or algorithmic variants) can be directly applied to lower levels of abstraction (assembly code or CUDA code) for future native implementations.

The developed algorithms are portable to di erent architectures if a tuned optimization of the matrix-matrix multiplication exists for those architectures.

Modularity and performance are two key goals in the development of linear algebra algorithms. Usually, the derivation of blocked algorithms is the first step towards the optimization of the performance of the implementation, improving data reuse and exploitation of the memory hierarchy in general-purpose architectures [70]. In addition to the performance boost, the usage of blocked algorithms also drives to modular algorithms, in which the operations performed on each block can be reformulated in terms of di erent BLAS-3 routines.

For example, the general matrix-matrix multiplication can be reformulated in terms of operations with sub-matrices of the original data. Figure 3.7 shows a possible algorithm for the matrix-matrix multiplication. At the beginning of the iteration, C0 and B0 have already been computed and used, respectively. In the current iteration, the next panel of matrix C is updated performing the operation C1 := C1 + AB1. Then, the preparation for the next iteration shifts C1 and B1 to the next blocks of data, increasing the number of columns in C0 and B0, since they contain more processed data at this point. This visual description, together with the three main stages involved in the algorithm (block definition, operations on blocks and data repartitioning), drives to the algorithm given in Figure 3.8 in FLAME notation.

As an illustrative implementation of the GEMM-based approach, we follow a similar blockoriented procedure as shown in Figure 3.7 for the blocked SYRK (symmetric rank-k update) implementation in BLAS-3. The conclusions and procedure applied to SYRK can be easily extended to the rest of BLAS-3.

The SYRK routine performs one of the two following rank-k updates:

C:= αAAT + βC,

C:= αAT A + βC,

where C is n × n, symmetric and stored as an upper or lower triangular matrix. The matrix A is n × k or k × n, respectively.

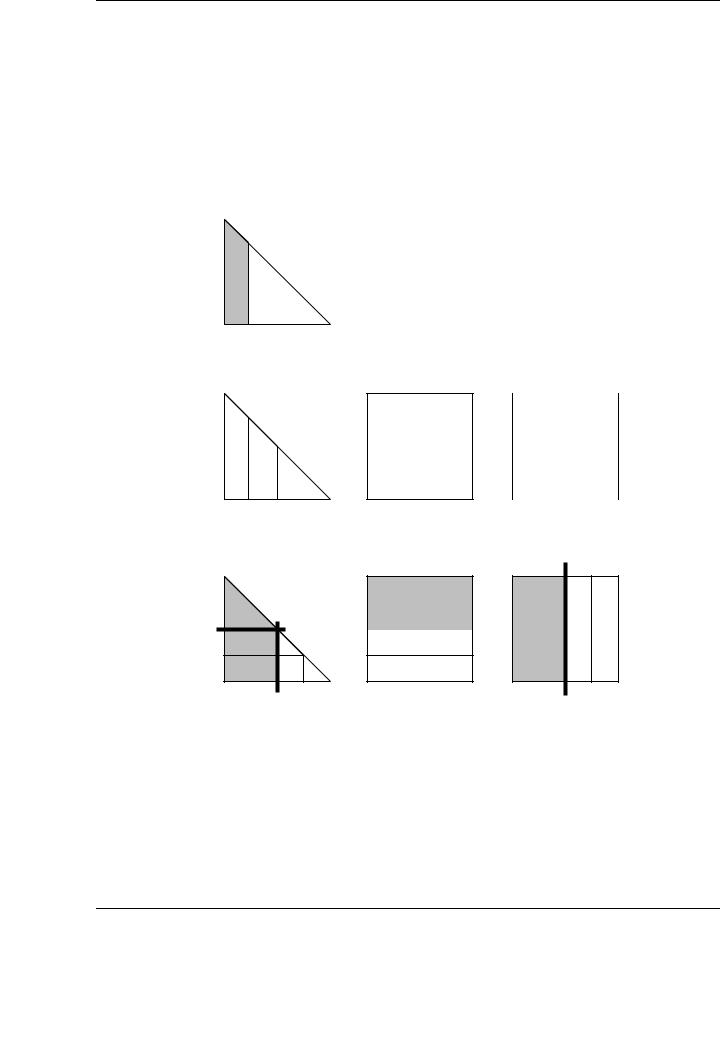
For each iteration of the blocked algorithm (see Figure 3.9), the update of the current block of columns of C involves two di erent tasks operating on two di erent blocks of C:

1.A diagonal block of the symmetric matrix C: C11 := C11 + A1AT1 .

2.An o -diagonal block of C: C21 := C21 + A2AT1 .

The operations involving the o -diagonal block of C can be carried out using the general matrixmatrix multiplication routine in BLAS (GEMM). Attending to the structure of the diagonal blocks, only those blocks must be updated using the rank-k update operation in BLAS (SYRK). Thus, in a major part of the iterations, most of the computation can be cast in terms of the highly tuned general matrix-matrix multiplication routine, and only certain blocks (in this case, the diagonal ones) need to be updated using the SYRK operation.

55

CHAPTER 3. BLAS ON SINGLE-GPU ARCHITECTURES

Step 1: Partitioning before iteration.

Step 2: Computation in iteration.

Step 3: Progress of partitioning in preparation for the next iteration.

Figure 3.7: A visualization of the algorithm for matrix-panel variant of GEMM.

56

3.3. IMPROVEMENTS IN THE PERFORMANCE OF LEVEL-3 NVIDIA CUBLAS

Algorithm: GEMM MP(A, B, C)

endwhile

Figure 3.8: Matrix-panel variant of the algorithm for computing the matrix-matrix multiplication.

The total number of flops for the SYRK routine is kn(n + 1) [12]. Defining a block size b, and considering the dimension n as a multiple of b, the number of flops to update each diagonal block of C (with dimension b × b) in the algorithm in Figure 3.9 is:

As there are nb diagonal blocks in C, the total number of flops cast in terms of the SYRK routine in the whole procedure is:

Therefore, the remaining operations are exclusively executed as general matrix-matrix opera-

Observe that, while the number of flops cast in terms of SYRK increases linearly with n (provided b n), the number of flops cast in terms of GEMM increases quadratically with this dimension. This relationship, or GEMM-fraction of the algorithm (in a similar way as the Level-3 fraction in [70]), will be critical for the final performance attained by the algorithm. From the results obtained from the evaluation of GEMM in the NVIDIA CUBLAS implementation, the exploitation of this amount of GEMM-based flops is expected to have a considerable impact in the final performance results of the new GEMM-based SYRK implementation.

57

CHAPTER 3. BLAS ON SINGLE-GPU ARCHITECTURES

Step 1: Partitioning before iteration.

Step 2: Computation in iteration.

Step 3: Progress of partitioning in preparation for the next iteration.

Figure 3.9: A visualization of the algorithm for matrix-panel variant of SYRK.

58