
М_Сухая, Бубнов. Задачи по высш. матем-ке Ч
.1.pdf1.4. ОБРАТНЫЕ МАТРИЦЫ. Н ЕВЫ РО Ж Д ЕН Н Ы Е СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Квадратная матрица А называется невырожденной, если ее опре
делитель отличен от нуля. . |
обратной |
квадратной невырожденной |
||
Матрица А ~’ называется |
||||
матрице А, если выполняется условие |
|
|
||
АА-' = А ~'А = Е. |
|
|||
Теорема. Для невырожденной матрицы А существует единственная |
||||
обратная матрица А ~ '. |
|
|
|
|
Если |
|
|
|
|
Он |
012 |
|
в Iп |
|
А = |
|
|
&2п |
|
|
|
|
|
|
4л1 |
&п2 |
|
|
|
то А 1 находят по формуле |
|
|
|
|
|
Аи |
^21 |
. |
А |
|
А и |
А22 |
. . |
А |
_Аы |
Aia |
. |
А |
|
где Дл = del A; Aij — алгебраические дополнения к элементам а,, матри цы А.
Рассмотрим |
систему п |
линейных |
уравнений |
с п неизвестными: |
||
|
в| iX\ + а12^2 + ... + а\пхп — b1,' |
|
||||
|
й2[^1 + Q22X2 -I- “Н а?пХп = 6г> |
( 12. ) |
||||
|
ал,Х! + а„?х2+... + ал„хл — Ь, |
|||||
|
|
|||||
где aih bi(i— 1, n, / = I, л) — действительные числа,}причем длякаждо |
||||||
го / имеется хотя бы одно а,,, отличное от нуля. |
|
|||||
Матрица |
|
|
|
|
|
|
|
|
|
ац |
аи |
din |
|
|
|
А = |
Я21 |
Й22 |
din |
|
|
|
|
АяI |
Йя2 |
|
|
называется матрицей системы (1.2). |
называется |
невырожденной. |
||||
Если det А |
0, то |
система |
(1.2) |
|||
Систему уравнений |
(1.2) можно записать в матричном виде: |
|||||
|
|
|
А Х ^ В , |
|
|
|
где X = [xt хч ... |
х„]т; |
В — (fr, |
6? ... |
bn). |
|
|
Упорядоченная система |
чисел (c'i, |
с2..... с„) называется решением |
||||
системы (1.2), если каждое из ее уравнений обращается в верное равенство после подстановки вместо xt, xt, .... лг„ чисел сi, с?, ..., с„ со ответственно. Матрица, составленная из этих чисел, называется векторрешением системы (1.2) и удовлетворяет матричному уравнению
АХ = В.
30
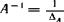
Невырожденная система п линейных уравнений с п неизвестными имеет единственное решение, которое может быть найдено по формулам Крамера:
х, — Д//Д, /= I. п.
где Д/ — определитель, полученный из определителя Д = det А заменой /-го столбца столбцом из свободных членов системы.
Решение системы (1.2) можно записать в матричном виде:
X = А~'В,
где А ~' — матрица, обратная к матрице А.
Метод нахождения решения системы (1.2) с использованием фор мулы X = А~ 'В называется матричным.
Примеры
1. Дана матрица
1 - 2 3
А = 4 0 5 -1 2 3
Найти матрицу А 1, если она существует. Реш ение. Вычисляем
ДЛ= 1-0-3 — 2-5{— 1}+ 4-2-3 — 3-0(— 1) +
+ 2- 4- 3 — 5-2-1= 48.
Так как Д^^О, то матрица Л -1 существует:
|
At\ |
А21 |
А$\ |
|
А Г2 |
А22 |
Аз2 |
|
j4js |
A23 |
А33 |
Находим |
дополнения: |
||
31
|
^ 23 — |
- |
l f + 3 |
|
1 |
— 2 |
'О, |
|
|
|
|
- |
1 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|||
|
Аз1 = |
- |
l )3+1 |
- |
2 |
3 |
= |
Ю, |
|
|
|
|
О |
? |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
А з2= |
_ |
1)3+2 |
1 |
3 |
— 7, |
|
|
|
|
|
4 |
5 |
|
|
|
|||||
|
|
|
|
|
|
|||||
|
/4зз — |
_ |
1)3 + 3 |
I |
- 2 |
= |
8 . |
|
|
|
|
4 |
|
О |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
Следовательно |
|
|
|
|
|
|
|
|
|
|
|
’ -10 |
12 |
- ю “ |
|
|
-5/24 |
1/4 |
-5/24' |
||
А-' — _L -17 |
6 |
7 = — 17/48 |
1/8 |
7/48 |
||||||
48 |
8 |
0 |
8 |
|
|
|
1/6 |
0 |
1/6 |
|
|
|
|
|
|||||||
2. Дана матрица |
|
|
|
|
|
|
|
|
||
|
А = |
1 |
|
- 3 |
|
4 |
|
|
|
|
|
- 3 |
|
5 |
|
6 |
|
|
|
||
|
|
|
- 2 |
|
2 |
|
10 |
|
|
|
Найти матрицу А |
|
если она существует. |
|
|
||||||
Реш ение. Так как |
|
|
|
|
|
|
|
|||
Ал=\ -5- 1 0 - 3 - 6 (- 2 )- 3 - 2 - 4 - 4 - 5 (- 2 ) +
+ 3(-3)* 10-1 -2-6 = 0,
то матрицы, обратной к А, не существует.
3. Дана система уравнений
2х\ — х% "I- Хз — 0 , |
3*1 — 2x2 — х3= 5, >
*1 + *2 +JC3= 6. J
Решить ее: а) матричным методом; б) по формулам Крамера.
Реш ение, а) Запишем матрицы:
2 |
-1 |
1 |
V |
А = *3 |
- 2 |
— I , |
в = 5 |
1 |
1 |
I |
6 |
Вычислим
Дд= 2 (- 2 ).1 + 3 .1 .1 + (- 1 ).1 + 1 2-1 -
— 1(— 1)*2— 3(— 1)•1= 7.
32
Найдем
Л] | —
Л|2 =
А 13=
Л21=
|
II |
|
II |
tfi |
|
М |
|
Лз) =
- 1 )1+' |
- |
2 |
1 |
- |
1 |
I |
= - 1, |
_|)'+ 2 |
3 |
|
|
- 1 |
|
= |
- 4 , |
|
1 |
|
|
1 |
|
||
_ 1)'+з |
3 |
|
|
- 2 |
|
= |
5, " |
|
1 |
|
|
1 |
|
|
|
- | )2+' |
- |
1 |
1 |
1 |
|
= 2, |
|
|
|
|
I |
|
|
|
|
- 1 )2+ 2 2 |
|
|
1 |
|
1 , |
|
|
|
1 |
|
|
1 |
|
|
|
_ l f + 8 2 — 1 |
|
= - 3, |
|||||
|
1 |
|
|
1 |
|
|
|
_ 1)3+1 |
- |
I |
- |
1 |
1 |
= 3, |
|
|
- |
2 |
|
|
|
||
<•> II V II
- 1 )3+2 2 |
1 |
- 5 , |
3 |
- 1 |
|
— 1)3+3 2 |
- 1 |
|
3 |
- 2 |
|
Тогда
- 1 |
2 |
3 |
- 4 |
1 |
5 |
5 - 3 - 1 |
|
|
Х = Л - ' В = 1/ |
" — 1 |
2 |
|
з ’ |
0 |
|
- 4 |
1 |
|
5 |
5 |
||
|
|
5 - 3 - 1 |
|
6 |
||
|
-1 •0 + 2•5 + |
3 •6 |
|
|||
|
— 4 * 0 + 1 *5 -j- 5 * 6 |
|
||||
|
5-0 — 3*5 — |
1-6 |
|
|||
28 |
|
4 |
, т. е. |
|
*i |
4 |
35 |
— |
5 |
|
Х2 |
= 5 |
|
—21 |
|
- 3 |
|
|
Хз |
'3 |
Отсюда х{ = 4, jc2 — 5, х3 = —3. б) Вычислим:
2-1699
|
0 |
- |
1 |
|
1 |
Ai — |
5 |
- 2 |
- |
= 6 + 5 + 12 + 5 = 28, |
|
|
6 |
|
1 |
|
|
Д2 = |
2 |
О |
|
1 |
= 10+ 18 -5+ 12 = 35, |
3 |
5 - 1 |
||||
|
1 |
6 |
|
1 |
|
|
2 |
- 1 |
0 |
|
|
Дз = |
3 - 2 |
|
5 |
— —24 — 5— 10+18= —21. |
|
|
1 |
|
1 |
6 |
|
Тогда по формулам Крамера:
= Д |/Д = 28/7 = 4, JC2 — Дг/Д = 35/7 = 5,
хъ= Д3/Д = -21/7= -3 .
4. Дана система уравнений
Х\ + Хг — 2хз»= 6Л |
\ |
|
2х\ + 3x2— 7х$(=1б,- |
||
5jti+2jf2+ хз»=I6- |
.J |
|
Решить ее: а) матричным методом; б) по формулам
Крамера.
Реш ение, а) Запишем матрицы А и В:
1 |
1 |
- 2 |
|
6 |
А = 2 |
3 |
- 7 |
, В = |
16 |
5 |
2 |
1 |
|
16 |
Г
Д * = 3 — 35 — 8 + 30 — 2 + 14 = 2,
Л п — ( — i f |
3 |
- 7 |
= 17, |
A i2 = ( - \ ? |
2 |
1 |
|||
A is = ( — 1)4 |
2 |
3 |
= - 1 1 , |
|
5 |
2 |
|
||
Ля = ( - 1)4| |
1 |
2 |
= 11, |
|
5 |
1 |
|
||
Л 3| = ( - 1)4 |
1 |
- 2 |
= - 1 , |
Лз2 = ( - ) ) 5 |
3 |
- 7 |
1 1
Лзз = ( - ! ) *
2 3
2 |
7 |
= -37, |
|
5 |
1 |
||
1 |
- 2 |
= -5, |
|
|
t |
|
|
|
|
= 3, |
|
1 |
- 2 |
= 3, |
|
2 |
- 7 |
||
|
34
Тогда
"Л,, |
Ац |
Лз1 |
в |
1 |
17 |
- 5 |
-1 |
Л12 |
А22 |
^ 3 2 |
-37 |
11 |
3 |
||
Л 13 |
Лгз |
Лзз |
|
♦ |
- И |
3 |
1 |
|
|
17 |
- 5 |
- Г |
" б‘ |
|
|
X — А ~ В = * -37 |
11 |
3 |
16 |
|
|||
|
|
-11 |
|
3 |
1 |
16 |
|
10280 - 16" |
( |
б' |
|
з ' |
|||
-222+176 + 48 |
__ |
2 |
=5 |
1 |
|||
- 6 6 + 48+ 16 |
|
2 |
- 2 |
— 1 |
|||
|
|
||||||
т.е. х\ = 3, Хг — 1, Хз ==— 1.
б) Вычислим:
6 I - 2
Л| = |
16 |
3 |
- 7 |
= 18112 — 64 + 96-16+ |
84 = 6, |
|
16 |
2 |
I |
|
|
|
1 |
6 |
- 2 |
|
|
д 2= |
5 |
16 |
- 7 |
= 16-64-210+160-12+112 = 2, |
|
|
16 |
1 |
|
|
|
|
! |
1 |
6 |
|
|
Аз = |
2 |
3 |
16 = 48+ 80 + 24— 90 — 32 — 32 |
= -2. |
|
|
5 |
2 |
16 |
|
|
По формулам Крамера имеем:
Х[ =6/2 =3, Х2= 2/2 = 1, Хз = —2/2— — 1.
5. С помощью формул Крамера решить невырожден
ную систему уравнений
|
|
2 jci + |
3jcj + |
11лсэ + |
5*4— 2 , |
|
|
||||
|
|
Х\ + |
|
*2+ |
5*3+ 2*4= 1, |
] |
|
||||
|
|
2xi + |
■*'2 + |
Здсз + 2x4, |
= |
' : |
f |
||||
|
|
|
—- з3, |
|
|||||||
|
|
X| + |
-*2+ |
Зхз + 4х4, —= |
—- 33. ) |
|
|||||
Реш ение. Вычислим: |
1 |
1 |
|
1 |
|||||||
|
2 |
3 |
11 |
5 |
0 |
|
|||||
А = |
1 |
1 |
|
5 |
2 |
1 |
1 |
5 |
|
2 |
|
2 |
1 |
|
3 2 |
0 |
— 1 - 7 - 2 |
||||||
|
1 |
1 |
|
3 |
4 |
0 |
0 |
- 2 |
|
2 |
|
35
|
|
|
|
|
|
,2+1 |
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
_ 1 |
_ 7 — 2 |
|
|||||
|
|
= K - 1 ) : |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0 |
— 2 |
2 |
|
|
|
|
|
= — ( — 14 + 2 — 4 + 2)= 14 |
|
|||||||||
|
|
|
2 |
3 |
|
11 |
5 |
|
0 |
1 |
1 |
1 |
|
Ai = |
|
1 |
"1 |
|
5 |
2 |
|
1 |
1 |
5 |
2 |
||
|
3 |
1 |
3 |
2 |
|
0 |
4 |
18 |
8 |
||||
|
|
|
3 |
I |
|
3 |
4 |
|
0 |
4 |
18 |
10 |
|
|
|
1 |
|
1 |
|
1 |
= - |
1 |
1 |
1 |
|
||
|
|
4 |
18 |
|
8 |
4 |
18 |
8 ^ |
- |
||||
|
|
4 |
18 |
10 |
|
|
0 |
|
0 |
2 |
|
||
|
2 |
|
2 |
|
11 |
5 |
|
0 |
|
0 |
1 |
1 |
|
Д 2 = |
I |
|
1 |
|
5 |
2 |
|
1 |
|
1 |
5 |
2 |
|
2 - 3 |
|
3 2 |
|
0 - 5 |
-7 - 2 |
||||||||
|
1 - 3 |
|
3 4 |
|
0 - 4 -2 |
2 |
|||||||
|
|
|
|
|
|
|
|
0 |
|
1 |
|
1 |
|
|
|
= l ( - l f |
|
-5 - 7 - 2 |
|
||||||||
|
|
|
|
|
|
|
|
-4 |
- 2 |
|
2 |
|
|
|
|
|
= - (8 + 1 0 ^ 28+10) = 0, |
|
|||||||||
|
S |
3 |
|
2 |
|
5 |
|
0 |
|
o |
0 |
1 |
|
Аз = |
1 |
1 |
|
1 |
|
2 |
|
1 |
|
1 |
1 |
2 |
|
2 1 - 3 2 |
|
0 - 1 |
--5 - 2 |
||||||||||
|
1 1 - 3 4 |
|
0 |
|
0 - -4 |
2 |
|||||||
|
)3 |
|
1 |
|
|
0 |
|
1 |
|
|
|
|
|
= 1 ( - |
-1 |
- 5 |
|
-2 |
= - (- 1 0 + 4 - 8 ) |
||||||||
1)3 |
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
- 4 |
|
2 |
|
|
|
|
|
|
|
2 |
3 |
11 |
|
|
|
|
0 |
|
1 |
|
0 |
|
Д4= |
1 |
1 |
|
5 |
|
|
1 |
|
1 |
|
1 |
5 |
1 |
2 |
I |
|
3 |
|
- 3 |
|
0 |
-1 |
- 7 |
- 5 |
|||
|
1 |
1 |
|
3 - 3 |
|
0 |
|
0 - 2 - 4 |
|||||
|
|
I |
|
1 |
|
|
0 |
|
|
|
|
|
|
= ( - l )3 |
— 1 |
- 7 |
|
- 5 |
= - (2 8 - 10 -4)= -14. |
||||||||
|
|
0 |
- 2 |
|
- 4 |
|
|
|
|
|
|||
36
По формулам Крамера имеем:
х\ = —28/14 = —2, * 2 = 0/14 = 0, ле3 = 14/14 = 1, л-4= — 14/14= — 1.
Задачи для самостоятельного решения
В задачах 1.65— 1.71 найти обратную матрицу для
данной матрицы.
|
. 1 |
2 |
|
1.65. А = ' |
|
|
|
1.66. А |
|
|
|
|
1 |
|
|
|
2 |
- 2 |
|
|
2 |
|
|
1.68. А = |
2 |
5 |
|
6 |
3 |
|
|
|
5 |
*—2 |
|
1.69. А = |
"з |
—4 |
5 |
2 |
- 3 |
I |
|
|
2 |
- 5 |
- 1 |
|
|
1 |
I |
1.70. А = |
|
1 |
— 1 |
|
- 1 |
1 |
|
|
|
||
|
|
— 1 |
— 1 |
|
|
|
1 |
Ответ: |
|
|
- 2 |
7 |
|
|
1 |
— 2 |
|
|
|
|
0 |
I |
|
’ |
1 |
- 4 |
- 3 ' |
Ответ: |
|
I |
- 5 - 3 |
|
|
-1 |
6 |
4 |
|
1/9 |
|
2/9 |
2/9 |
|
2/9 |
|
1/9 -2/9 |
||
2/9 |
|
-2/9 |
1/9 |
|
|
|
1 |
- 1 |
1 |
|
-38 |
41 |
-34 |
|
|
37 -29 |
24 |
||
|
-8 |
29 -11 |
||
Ответ: |
- 5 |
|
18 |
—7 |
|
|
|
- 3 |
1 |
1
—1
1
1
Ответ: — 1 |
I |
- 1 |
- |
|
- 1 |
|
I — |
||
1 |
- 1 |
- 1 |
|
|
|
1 |
о |
о |
|
К71. А = |
2 |
0 |
0 |
|
1 |
3 |
4 |
||
|
||||
|
— 1 2 |
3 |
||
37
|
2 |
- I |
О |
О |
) |
|
Ответ: |
- 3 |
2 |
О |
О |
||
31 |
- 1 9 |
3 |
- 4 |
|||
|
||||||
|
-23 |
14 |
— 2 |
3 |
В задачах 1.72, 1.73 найти неизвестную матрицу X из данного уравнения.
~1 |
1 |
-1 |
[1 |
-1 |
з ' |
1.73. X 2 |
1 |
0 = |
4 |
* 3 |
2 |
1 |
- I |
1 |
ь |
- 2 |
5 |
( |
- 3 |
2 |
Ответ: - 4 |
5 |
|
|
- 5 |
3 |
В задачах t.74— 1.86 проверить, является ли система
линейных уравнений невырожденной, и решить ее по фор
мулам Крамера и матричным методом.
|
( 2х\ + |
3x2— |
*з = 4, |
||||
1.74. < |
*i + |
|
*2 + 3*3 = 5, |
||||
|
( . 3 * , - |
|
4*2 + * з |
= 0. |
|||
|
|
(Ответ: [1 |
1 |
1]г.) |
|||
1.75. |
|
*1 — |
|
*2 — *3 = |
|
о, |
|
|
* 1 + |
2 * 2 + * 3 = |
|
] , |
|||
|
|
|
|
*2 —-*3 = — 3. |
|||
|
{(Ответ: [1 |
-1 |
|
2]г.) |
|||
|
|
*[ + |
|
2*2 + 3*з = |
1, |
||
|
|
5*[ + 8*2 — |
*з = 7, |
||||
|
{2*i — |
3*2 + 2*з = 9. |
|||||
|
|
(Ответ: [3 |
— 1 |
0)г.) |
|||
к |
|
*1 + 5*2 + |
*з = |
0, |
|||
|
2 *| — |
4*2 — 3*з = |
— 1 , |
||||
|
{ |
3*i + 4*2 + 2*з = 8. |
|||||
38 |
(Ответ: [2 -1 3]г.) |

