16.1.1 Методы вычисления интегралов. Формулы трапеций и Симпсона

Для приближенного вычисления интегралов существует много разных методов. Пусть надо найти:

Для вычисления интеграла Мора часто используют метод Верещагина. Однако более удобными являются приближенные методы.

Рис. 16.5

Формула трапеций

Разобьем интервал на малые интервалы (например, на рис.16.5. их четыре).

Поскольку по геометрическому смыслу интеграл представляет собой площадь фигуры mnkl, то С можно вычислить приближенно, представив ее в виде суммы площадей четырех трапеций:

(16.3)

Формула Симпсона

Формула Симпсона намного точнее формулы трапеций (хотя может показаться менее удобной). Она имеет вид:

(16.4)

При этом в отличие от метода трапеций, отрезок а должен разбиваться на равные интервалы . Аналогично, должно быть

Примечание. Для прикидочных грубых оценок можно использовать формулу:

.

2. . Вычисление прогибов на основе решения дифференциального уравнения изогнутой оси балки

Прогибы можно находить и другими способами, например, на основе решения дифференциального уравнения изогнутой оси балки. Для вывода этого уравнения, рассмотрим элемент балки (рис.16.6).

Рис. 16.6

Ясно, что чем больше , тем больше кривизнаизогнутой оси балки.

Эту фразу можно записать в виде:

. (16.5)

Выразим кривизну через прогиб. Согласно формулам математического анализа:

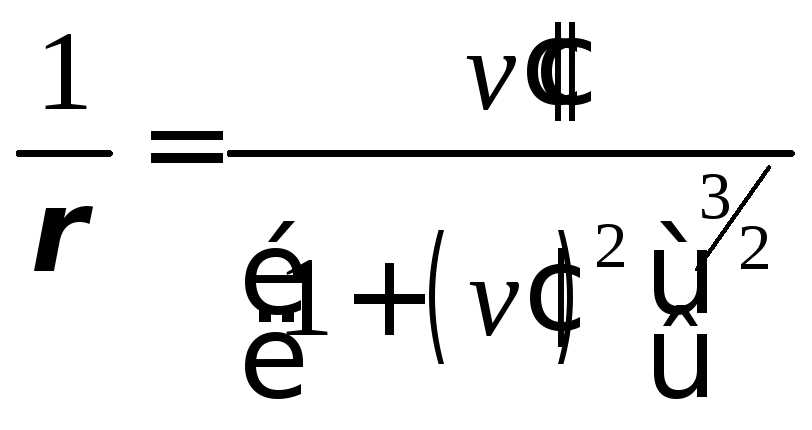
Рис.16.7

По геометрическому смыслу производная это тангенс угла наклона кривой (рис16.7):

.

Ввиду малости прогибов угол также мал, поэтому

.

Тогда: (16.6)

Очевидно, что k зависит от геометрии сечения и материала балки. Найдем эту зависимость.

Рассмотрим малый элемент балки длины (рис. 16.3, 16.4). После изгиба он превратится в изогнутый элемент (рис.16.8). Длина волокнаBC, которое проходит через центр тяжести сечения, не изменяется и будет равна . А нижнее волокноDH удлиняется на .

Рис.16.8

Вычисляем , учитывая, что. Согласно определению

.

Используя закон Гука и формулу Навье получаем

. (16.7)

Вычислим теперь по другому - через угол(рис.16.8). Из геометрии известна формула для вычисления длины дуги:

.

Тогда

. (16.8)

Приравниваем (16.7) и (16.8):

.

Отсюда получаем:

.

Учитываем, что согласно (16.6):

Окончательно получаем:

(16.9)

Это и есть уравнение изогнутой оси балки.

16.2.1 Решение дифференциального уравнения изогнутой оси балки

Если балка имеет постоянную толщину, то есть , то решение легко записывается в общем виде:

(16.10)

(16.11)

Хотя решение получено в общем виде, однако основная трудность заключается в определении М_х и констант C и D, поскольку на разных участках балки разные, а значитC и D также разные (в частности, если балка имеет три участка, то нужно определить 6 констант C и D).

Однако существует способ интегрирования, который сводит все неизвестные только к двум константам (разработан Клебшом)

16.2.2 Правила Клебша

Правила Клебша сводятся к следующему.

1) выражаем через внешние силы, которые лежат только слева (или только справа) от сечения.

2) Если погонная сила q не доходит до правого конца, то ее доводим до этого правого конца и уравновешиваем ее снизу (рис.16.9)

Рис.16.9

3) Если имеется сосредоточенный момент m_о, то его вклад записываем в виде , гдеа - расстояние до момента m_о.

4) Интегрируем, не раскрывая скобок.

При выполнении этих условий все константы С на разных участках будут одинаковы. Аналогично будут одинаковы все константы D.

Справедливость правил Клебша доказывается непосредственной проверкой, то есть подстановкой решения в условия стыковки решения на границе участков. Рассмотрим, например, случай, приведенный на рис.16.12.

рис16.12

По правилам Клебша момент на участках (1), (2) запишем в виде:

(1):

(2):

Дифференциальные уравнения на участках:

(1)

(2)

Решение этих уравнений на участках (1), (2) имеет вид:

Участок (1): .

Участок (2): .

Отсюда видно, что при S = a получим равенство углов наклона и прогибов, вычисленных по разным формулам при любых С и D, т.е. условия гладкости изогнутой оси выполняются. Аналогично проверяются условия гладкости на границе участка, на которой заканчивается погонная сила q.