К статье н.И. Лобачевского «значение некоторых определенных интегралов» Грачева в.А., Бутова о.Н., Кулиев в.Д.

Н.И. Лобачевским в этой статье [1] получены оригинальные результаты. Мы продолжим начатый Н.И. Лобачевским исследования.

§1. Теоремы н.И. Лобачевского и новая теорема

Имеет место

Теорема 1. (Н.И. Лобачевский). Если функция f(x) 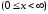удовлетворяет условиям

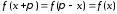(1.1)

и если существует интеграл

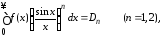
то

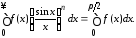(1.2)

Доказательство. Представим интеграл в виде суммы ряда

Пусть 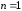. Положив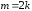или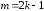и прибегнув, соответственно, к подстановке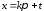или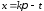, в силу (1.1), будем иметь:

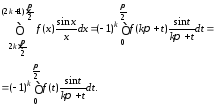
Отсюда

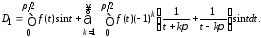
Так как ряд

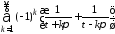
В промежутке 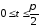сходится равномерно, ибо мажорируется сходящимся рядом

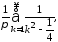
то его можно интегрировать почленно.

Следовательно,

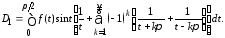
Но выражение в квадратных скобках есть разложение на простые дроби функции .

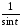Таким образом, окончательно имеем

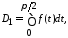
что и требовалось доказать для случая .

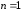Пусть теперь 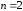. Поступая точно так же, как для случая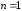, получаем

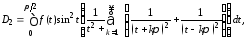
откуда замечая, что

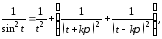
находим

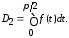
Теорема доказана.

Замечание 1. Определим сумму ряда

т.е. докажем, что

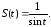
Функцию 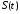можно представить в виде:

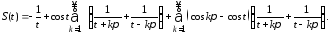
Последний ряд удовлетворяет всем требованиям формулы суммирования Плана [2].

Имеем

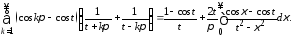
Замечая, что для любого конечного (см. ниже (2.2)):

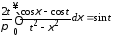
и

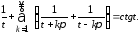
Окончательно, находим

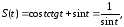
что и требовалось доказать.

Теорема 2. (Н.И. Лобачевский). Если функция f(x) удовлетворяет условиям

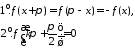(1.3)

(условия непрерывности функции 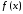в точках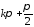, где

и если существует интеграл, то

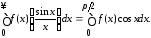(1.4)

Доказательство. Поступая точно так же, как при доказательстве теоремы 1 (Н.И. Лобачевский), получаем

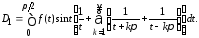
Отсюда, замечая, что

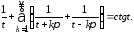
приходим к (1.4). Доказательство закончено.

Теорема 3. Если функция 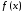удовлетворяет условиям теоремы 2 (Н.И. Лобачевский) и если существует интеграл

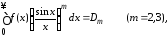
то

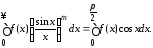(1.5)

Доказательство. Поступая точно так же, как при доказательстве теоремы 1 (Н.И.Лобачевский), в силу (1.3) получаем

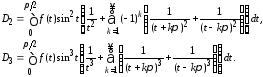
Отсюда, замечая, что

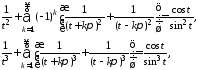
приходим к утверждению теоремы 3 (1.5).

§2. Некоторые утверждения и примеры

Следует указать, что справедливы следующие утверждения:

1. Формула Лобачевского (1.2) остается в силе и в том случае, когда функция f(x) в промежутке 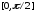интегрируема в несобственном смысле (при сохранении прочих условий теоремы 1Лобачевского).

2. Формула Лобачевского (1.4) и формула (1.5) также остаются в силе в том случае, когда функция f(x) в промежутке 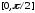интегрируема в несобственном смысле (при сохранении прочих условий теоремы 2Лобачевского и теоремы 3, если функция f(x) в точке непрерывна; если же функцияf(x) в точке 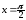имеет интегрируемую особенность, то условие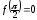отпадает, а остальные условия теоремы 2Лобачевского и теоремы 3 при этом сохраняются).

Следствие вышеперечисленных теорем:

1. Если , то из формулы Лобачевского (1.2) следует, что

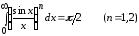(2.1)

2. Если , гдеm – любое целое число, то из (1.2) следует, что

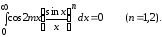
3. Если 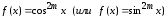, то из (1.2) приходим к формулам Валлиса

~

~

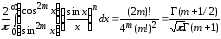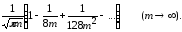
4. Если 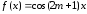, гдеm=0, ±1,…, то из (1.4) и (1.5) следует, что

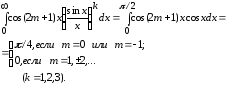
Примеры.

1°. Рассмотрим интеграл

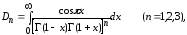
где Г(t) – гамма-функция Эйлера. Благодаря тому, что

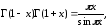
интеграл 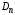допускает применение теоремы 2 и теорема 3 без труда вычисляется

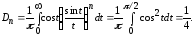
Отметим, что при n=2 интеграл 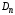является частным случаем интеграла Рамануждана.

Теперь вычислим этот интеграл при n=2 с помощью теоремы 1 Лобачевского. Выполнив в интеграле

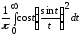
интегрирование по частям, получим

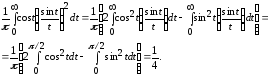
Чтобы вычислить этот интеграл при n=1, следует воспользоваться результатами теорем 1 и 2 Лобачевского. Вычисления дают

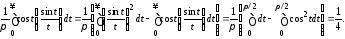
Отметим, что используя этот интеграл (при n=2) можно показать, что

Действительно,

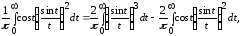
откуда следует

Теперь остается учесть, что

чтобы получить искомое равенство

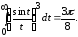
Исходя из равенства

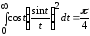
и выполнив в левой его части интегрирование по частям, находим значение еще одного интеграла

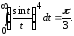
2°. С помощью теоремы Лобачевского докажем, что для любого конечного t

(2.2)

Доказательство. Сначала рассмотрим случай t>0. Имеем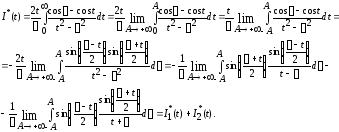

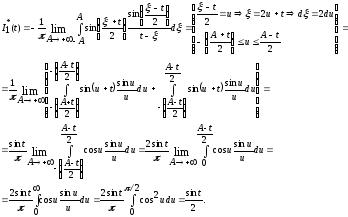
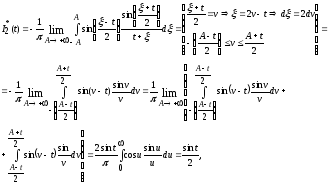
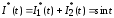
Аналогично доказывается случай t<0.

Пусть теперь t=0. Докажем, что в этом случае

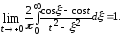
Действительно,

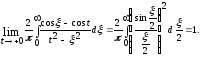
Доказательство закончено.