matem-up1

28.M (2 3 , 3 ).

12.Образец контрольного задания

векторами br = (3, − 1), cr = (1, 2). В ответе указать сумму коэф

фициентов разложения.

129

br = ir − 2 rj − 2kr .

6. Найти скалярное произведение (ar − br)(2ar + br), если

ar = 1, br = 3, ar br .

7. Найти площадь ∆ABC , если

A(7 , 3, 4), B(1, 0, 6 ), C (4, 5, − 2).

8. Найти объём пирамиды с вершинами

O (0, 0, 0), A(5, 2, 0), B(2, 5, 0), C (1, 2, 4).

130

Раздел 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

1. Координатный метод. Уравнения линий и

поверхностей

В основе аналитической геометрии лежат идеи использо вания координатного метода и понятия уравнения линии или поверхности.

Идея координатного метода состоит в том, чтобы указы вать положение точки на плоскости или в пространстве с помо щью чисел. Наиболее удобной для этой цели является прямо угольная декартова система координат. Напомним, что положе ние точки на плоскости задаётся двумя числами – абсциссой и ординатой, положение точки в пространстве – тремя числами – абсциссой, ординатой и аппликатой.

В аналитической геометрии линии и поверхности рассмат риваются как множества точек, обладающих некоторым, только им присущим свойством. Например, окружность определяется как множество точек плоскости, равноудалённых от некоторой фиксированной точки на этой плоскости (центра окружности);

сферу можно рассматривать как множество точек в пространст ве, равноудалённых от некоторой фиксированной точки про странства (центра сферы).

119

Равенство F (x, y) = 0 с двумя переменными x, y называ ется уравнением линии L на плоскости с системой координат

OXY , если координаты любой точки линии удовлетворяют этому равенству, и, наоборот, любая точка, координаты которой

удовлетворяют этому равенству, лежит на линии L. Короче,

F (x, y) = 0 M (x, y) L .

Таким образом, уравнение линии L есть соотношение, свя зывающее координаты точек данной линии (и только этих то чек). Конечно, если рассмотреть на плоскости другую систему

координат, то эта линия будет иметь другое уравнение.

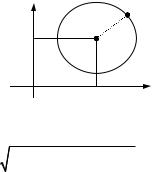
Пример 4.1. Вывести уравнение окружности с центром в точке M0 (x0 , y0 ) и радиусом R.

Решение. Пусть M(x, y) – любая точка окружности L. Тогда,

используя определяющее свойство точек окружности, можно

символически записать:

окружности запишем в виде:

(x − x0 )2 + (y − y0 )2 = R .

120

Таким образом, координаты x, y каждой точки М окруж ности удовлетворяют уравнению

(x − x0 )2 + (y − y0 )2 = R2 .

Обратно, любая точка M (x, y), координаты которой удовлетворяют этому уравнению, принадлежит окружности, так как её расстояние от точки M0 (x0 , y0 ) равно R.

Аналогично вводится понятие уравнения поверхности в

странстве, если для любых чисел x, y, z данное равенство спра ведливо тогда и только тогда, когда точка M(x, y, z) лежит на по верхности Р :

F (x, y, z) = 0 M (x, y, z) P .

Замечания.

1) В дальнейшем будут рассмотрены только линии и по верхности, определяемые в прямоугольной системе координат алгебраическими уравнениями первой и второй степеней. На пример, на плоскости:

Ax + By + C = 0 – уравнение 1 й степени (хотя бы одно

из чисел A, B не равно 0);

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 – уравнение 2 й сте

пени (хотя бы одно из чисел A, B, C не равно 0).

121

Примером пространственной линии, заданной параметри чески, может служить винтовая линия:

x = R cos t , y = R sin t , z = ht .

Если параметр t рассматривать как время, то такую линию

будет описывать точка, которая равномерно движется по обра зующей кругового цилиндра радиуса R, в то время как сам ци линдр равномерно вращается вокруг своей оси.

2. Прямая на плоскости

Рассмотрим на плоскости OXY простейшую линию – пря мую. Уточним понятие «прямая», указав свойство, присущее

только точкам этой линии.

Пусть М0 – точка, n – некоторый ненулевой вектор на плос кости OXY . Прямой L называется множество точек М плоскости

В этом случае говорят: прямая L задана точкой М0 и векто ром нормали nr .

Теорема 4.1. Прямая на плоскости OXY и только она мо жет быть задана уравнением 1 й степени:

Ax + By + C = 0 .

123

Доказательство. « ». Пусть L – прямая, М0(x0 , y0) – точка плоскости, nr = (A, B)– вектор нормали прямой. Запишем усло вие того, что произвольная (текущая) точка М(x, y) лежит на прямой L:

Последнее соотношение (полученное как результат вычис ления скалярного произведения в координатной форме) есть уравнение прямой. Если раскрыть скобки и обозначить число

(–Ax0 – By0) буквой C, то получим: Ax + By + C = 0, что и требова

лось.

« ». Рассмотрим уравнение 1 й степени:

Ax + By + C = 0 . Возьмём точку М0(x0 , y0), координаты которой удовлетворяют данному уравнению: Ax0 + By0 + C = 0. Вычитая из 1 го уравнения последнее равенство, получим: A(x – x0) + B(y

– y0) = 0.

Из первой части доказательства видно, что это уравнение задаёт прямую, проходящую через точку М0(x0 , y0) перпендику лярно вектору nr = (A, B). Итак, уравнение Ax + By + C = 0 за даёт прямую. Теорема доказана.

Замечание. Уравнение Ax + By + C = 0 называют общим уравнением прямой на плоскости. Если это уравнение дано, то известен вектор нормали nr = (A, B). Обратно, если известен

124

вектор нормали, то, зная хотя бы одну точку прямой, можно за писать её уравнение.

Пример 4.2. Написать уравнение прямой, проходящей че рез точку М0(1 , –2) перпендикулярно вектору nr = (2, 1) .

Решение. Так как вектор нормали известен, то уравнение прямой можно записать в виде: 2 x + y + C = 0 . Точка М0(1, –2)

лежит на прямой, поэтому её координаты должны удовлетво рять этому уравнению: 2 1 − 2 + C = 0 . Отсюда C = 0 . Итак,

уравнение прямой: 2 x + y = 0 .

Отметим, что уравнение прямой можно записать сразу в виде:

2 (x − 1)+ 1 (y + 2) = 0 2 x + y = 0 .

Рассмотрим частные случаи общего уравнения прямой.

1) Если А = 0, то n OX , L || OX . Уравнение прямой

принимает вид By + C = 0 или y = − CB (горизонтальная пря мая). При условии A = C = 0 получим уравнение оси OX: y = 0.

2) Если В = 0, то n OY , L || OY . Уравнение прямой име

ет вид Ax + C = 0 или x = − CA (вертикальная прямая). При

B = C = 0 получим уравнение оси OY: x = 0.

125

3) Если B ≠ 0 , то уравнение прямой можно записать в виде

Значит, k – тангенс угла ϕ между прямой и осью OX (угло вой коэффициент прямой). Угол отсчитывается от положи тельного направления оси OX против часовой стрелки.

Уравнение прямой

y = kx + b

называется уравнением с угловым коэффициентом. Отметим,

что в такой форме можно записать любую невертикальную

прямую.

Замечание. Уравнение y = kx + b можно записать в форме

общего уравнения прямой: kx − y + b = 0 . Вектор нормали nr = (k , − 1).

126