
matem-up1
.pdf
мах OXY и О1X1Y1 соответственно. Рассмотрим векторы:
uuuur |
r |
|
r |
uuuur |
r |
|
OM = x i |
+ y j , |
OO1 = a i |
+ b j , |
|
||
uuuuur |
|
r |
r |
|
|
|
O1 M |
= x1i |
+ y1 j . |
|
|
||
|
uuur |
|
uuuuur |
uuuur |
|
|
Так как OM |
= O1 M |
+ OO1 , то |
|
|
||
|
|
|
x = x + a, |
x = x − a, |
||
|
|
|
{y = y11 + b |
или {y11 |
= y − b. |
|
Полученные формулы параллельного переноса позволя ют находить старые координаты (x, y) любой точки по новым координатам (x1, y1) и наоборот.
Пример 3.15. Начало координат перенесено в точку
О1(–1, 2). Найти новые координаты точки M (3, − 2).
Решение. По формулам параллельного переноса опреде ляются новые координаты точки М:
{x1 = x −(−1) = 3 + 1 = 4, y1 = y − 2 = −2 − 2 = −4.
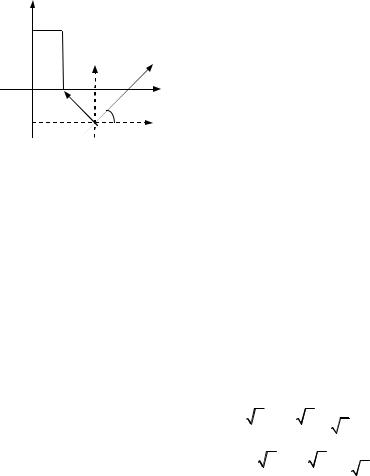
Случай 2. Начало координат оставим неизменным, а базис
|
Y1 |
|
Y |
|
|
M |
i , rj |
изменим, |
повернув каждый |
||
|
|
r |
|
|
|
|
ϕ (против часовой |
||||
|
|
|
|
|
вектор на угол |
||||||
|
|
|
|
|
X1 |
||||||
r |
|
j |
ir1 |
|
|
|
|
|
|||
j1 |
|
|
|
стрелки, |
если |
ϕ > 0 ; |
по часовой |
||||
|
|
|
|
ϕ |
X |
стрелке, |
если ϕ < 0 ). |
Новый базис |
|||
|
|
|
|
|
|
||||||
|
|
O |
|
ir |
|
||||||
|
|
|
|
i1 , rj1 |
также является ортонорми |
||||||
|
|
|
|
|
|
|
|||||
рованным и будет порождать новую систему координат ОX1Y1.
119
Пусть точка М имеет в старой системе координаты (x, y), а в
uuur
новой – (x1, y1). Вектор OM можно разложить по старому и но вому базисам:
uuuur |
r |
r |
r |
|
OM = x i |
+ y j |
= x1i1 |
+ y1 j1 . |
( ) |
Умножим равенство ( ) скалярно на вектор i : |
|
|||
x ir ir + y rj ir = x1ir1 ir + y1 rj1 ir . |
|
|||
Имеем: |
|
|
|
|
ir ir = 1, rj ir = 0, ir1 ir = cosϕ , |
rj1 ir = cos(90o +ϕ)= −sinϕ . |
|||
Поэтому x = x1 cosϕ − y1 sinϕ.
Аналогично, умножим равенство ( ) скалярно на вектор rj : x ir rj + y rj rj = x1ir1 rj + y1 rj rj . Учитывая, что i rj = 0, rj rj = 1, ir1 rj = cos(90o −ϕ)= sinϕ , rj1 rj = cosϕ , имеем
y = x1 sinϕ + y1 cosϕ.
Итак, формулы поворота системы координат
x = x1 cosϕ − y1 sinϕ ,y = x1 sinϕ + y1 cosϕ
позволяют найти старые координаты (x, y) через новые (x1 , y1).
Отсюда легко получить формулы для перехода от коорди нат старых (x, y) к новым (x1 , y1):
x1 = x cosϕ + y sinϕ ,y1 = −x sinϕ + y cosϕ.
120
Y |
|
|
|
Пример 3.16. Зная координа |
|
|
|
|
|
2 |
|
M |
|
ты точки М(1, 2) в декартовой сис |
|
|
Y1 |
X2 |
теме OXY, найти её координаты в |
|
1 |
2 |
новой системе координат, полу |
|
O |
Y2 |
450 X |
ченной из данной переносом на |
|
–1 |
|
|
O1 X1 |
|
|
|
|
чала О в точку О1(2, –1) и поворо |
|
|
|
|
|
|
том осей на угол 45°. |
|
|||
Решение. Здесь можно рассмотреть три системы коорди нат, представленные на рисунке. Пусть точка М имеет коорди
наты (x, |
y), (x1, y1), (x2, y2) |
соответственно в системах OXY , |
|
O1 X1Y1 , |
O1 X 2Y2 . По условию задачи: x = 1, |
y = 2 . По форму |
|
лам |
параллельного |
переноса |
получаем: |
{x1 = x −(2 =)1 − 2 = −1, y1 = y − −1 = 2 + 1 = 3.
Координаты (x2, y2) вычисляем по формулам:
|
|
|
|
|
|
sin45o = (−1) |
2 |
|
|
|
2 |
|
|
|
|||
x |
|
= x |
|
cos 45o + y |
|
+ 3 |
|
= 2 , |
|||||||||
|
|
2 |
|
2 |
|
||||||||||||
|
2 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
y |
2 |
= −x |
1 |
sin45o + y |
1 |
cos 45o = −(−1) |
|
|
+ 3 |
|
= 2 2 . |
||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9.Контрольные вопросы
1.Какие векторы называются коллинеарными, равными,
компланарными?
121
2. Как выполняется сложение векторов и умножение век тора на число?
3. Что называется проекцией вектора на ось? Какими свой ствами обладают проекции?
4. В каком случае векторы называются линейно зависимы ми и в каком – линейно независимыми?
5. Какое максимальное количество векторов может со держать линейно независимая система векторов на плоскости?
6. Какое максимальное количество векторов может со держать линейно независимая система векторов в пространст ве?
7.Что называется базисом на плоскости и в пространстве?
8.Какой базис называется ортонормированным?
9.Что такое прямоугольные декартовы координаты векто
ра на плоскости и в пространстве?
10.Как определяются координаты точки?
11.Как, зная координаты вектора, определить его длину и направление?
12.Как вычислить координаты вектора по известным ко
ординатам его конца и начала?
13. Как найти расстояние между двумя точкам с известны ми координатами?
14. Каким образом определяются координаты точки, кото рая делит отрезок в заданном отношении?
122
15. Что называется скалярным произведением векторов,
каковы его свойства?
16. Как вычисляется скалярное произведение в коорди
натной форме?
17.Как найти угол между двумя векторами, заданными в координатной форме?
18.Что называется векторным произведением векторов,
каковы его свойства?
19. Как вычисляется векторное произведение в коорди натной форме?
20. Как можно вычислить площадь параллелограмма, по строенного на векторах?
21. Что называется смешанным произведением векторов,
каковы его свойства?
22. Как вычисляется смешанное произведение в коорди натной форме?
23. Какие применения смешанного произведения Вы знае
те?
24. Какое изменение системы координат называется па раллельным переносом? Как при этом изменяются координаты точки?
25. Как изменяются координаты точки на плоскости при повороте координатных осей на угол ϕ?
123

10.Упражнения
1.В треугольнике ABC сторону АВ точками М и N разделили
uuur
на три равные части: AM = MN = NB. Найти вектор CM , если
uuur |
r |
uuur |
r |
|
|
CA = a , |
CB |
= b . |
|
|
|
|
2. Дана равнобедренная трапеция ABCD, в которой |
m – |
|||
единичный вектор в направлении вектора основания |
uur |
n – |
|||
AB , |
|||||
единичный вектор в направлении вектора стороны |
uur |
угол |
|||
AD , |
|||||
между этими векторами α = 45o , длина основания AB=8, длина
боковой |
стороны |
AD = 3 2 . Разложить |
векторы |
сторон |
|
uur uuur |
uuur |
uuur |
uur |
uuur |
|
AB, BC , CD, |
DA и векторы диагоналей AC , |
BD по век |
|||
торам m и n . |
|
|
|
|
|
3. Найти длину и направляющие косинусы вектора |
uur |
||||
AB , ес |
|||||
ли A(−1, 2), B(3, − 2).
4. Радиус вектор точки M(x, y, z) составляет с осью OX угол
uuuur
α = 60o , с осью OZ угол γ = 45o , длина вектора OM = 8 , а его координата y > 0. Найти координаты точки M.
5. Даны векторы ar1 = 2i + 3 rj − kr и ar2 = (1, 0, 2). Опреде
лить:
а) проекции на координатные оси вектора a = 2ar1 − 3ar2 ;
б) координаты вектора b , который коллинеарен вектору ar1
124

и | b | =7 2 ;
в) орт вектора ar2 .
6. Даны векторы ar = (1, 0, 1) и b = (−2, 3, 5). Будут ли век
торы cr1 = ar + 2b и cr2 = 3ar − b коллинеарными?
7. Докажите, что векторы b = (−1, 1) и cr = (1, 2) образуют
базис на плоскости. Найти разложение вектора |
ar = (2, 1) по |
||||||||
этому базису. |
|
|
|
|
|
|
|
||
|
8. Докажите, |
|
r |
(1, 1, −1), |
r |
−1, 1) |
|||
|
что три вектора p = |
q = (1, |
|||||||
и |
rr = (−1, 1, 1) |
образуют базис в пространстве. Разложить век |
|||||||
тор ar = (36 , 13,7 ) по этому базису. |
|
|
|
|
|||||
|
9. Найти скалярное произведение векторов c |
и d , если: |
|||||||
|
r |
r |
r |
r |
|
| b |= 3 |
r |
|
|
|
а) c |
= 5a + |
3b |
, d = 2a − b , | a |= 2 , |
, a b ; |
|
|||
|
б) cr = 3ar − 2b , d = ar + 4b , | a |= 1 , | b |= 4 , (ar,br)=π / 3 . |
||||||||
|
10. Пусть |
|
| a1 | = 1 , |
| a2 | = 3 , |
(ar1 ,ar2 ) = 3π / 4 , |
||||
r |
r |
r |
r |
r |
|
|
|
|
|
m = 3a1 |
+ 2a2 , |
n |
= a2 − a1 . Найти: а) длину вектора m ; |
б) ко |
|||||
синус угла между векторами m и n ; |
в) проекцию вектора m |
||||||||
на ось, определяемую вектором n . |
|
|
|
|
|||||
|
|
|
|
r |
|
r |
|
|
|
|
11. Даны векторы m = (2, − 1, 3) и n = (3, 6 , − 2) . Вычис |
||||||||
лить:
125

а) m n ; |
r |
r |
r |
r |
б) (2m |
− n) ( |
3m |
+ 2n); |
|
r r |
|
r r |
|
|
в) прnr (m + n); |
г) cos (m, n). |
|
||
12. Найти вектор |
m , коллинеарный вектору nr = 3i + j − k |
|||
и удовлетворяющий условию m n = 22 .
13. Вектор b , перпендикулярный вектору ar = (1, − 2) , об разует острый угол с осью OX. Найти его координаты, если
| b | = 20 .
14. Найти работу А, произведённую силой F = 3i − 5 rj + kr ,
если её точка приложения перемещается прямолинейно из по ложения M(1, 3, 2) в положение N(2, –1, 0). Под каким углом ϕ к перемещению направлена сила?
15. Найти | (2ar +br)×(br − 3ar)| , если | a | = 3 , | b | = 2 ,
(a,br r)= 450 .
16. Вычислить площадь параллелограмма, построенного на векторах ar + 3b и 3ar + b , если | ar | = | b | = 1, (ar, br)= 300 .
17. Даны векторы ar = 2i − 4 j − k , b = i − 5 j + k . Найти векторное произведение (2ar − br)×(ar + br).
18. Найти координаты единичного вектора, перпендикуляр
r |
r |
+ 4 j − k . |
ного векторам m = −3 j + k |
и n = −i |
126
19. |
Найти координаты |
вектора n , |
|
r |
r r |
|||
если n a , n b , |
||||||||
|
r |
|
r |
|
(0, 1, 1), тройка |
r |
r |
|
|
n |
= 10, a = (1, 2, − 3), b = |
a , b , n – левая. |
|||||
20. |
Силы F1 = (4,7 , − 11), F2 = (5, − 2, 8) |
приложены к точ |
||||||
ке C(6, – 4, –5). Найти величину и направляющие косинусы мо |
||||||||
мента M равнодействующей этих сил относительно начала ко |
||||||||
ординат. |
|
|
|
|
|
|||
21. |
Даны вершины треугольника A(2, 1, –1), B(1, 0, 3), |
|||||||
|
C(2, –2, 5). Найти: |
а) длины сторон AB, AC, BC; |
б) B ; |
|||||
|
|
|
в) площадь ∆ABC ; |
|
|
|
|
|
|
|
|
г) высоту треугольника h, опущенную из вершины B; |
|||||
|
|
|
д) координаты M – точки пересечения медиан треуголь |
|||||
|
|
ника. |
|
|
|
|
|
|
22. |
Найти смешанное произведение векторов |
|
||||||
|
|
|
ar = (−1, 2,7 ), b = 4i + 3 j − k , cr = j − 3k . |
|||||
23.Определить, левой или правой является тройка векто ров:
ar = i + k , b = j , cr = (2, 1, 3).
24. При каком значении λ векторы ar = (−1, 4, 8),
b= (λ , 2, 3), cr = (2, − 1, − 5) компланарны?
25.Лежат ли точки A(1, 2, –1), B(2, 1, 3), C(1, 2, 1),
127

D(0, 1, 5) в одной плоскости?
26. Вычислить объём параллелепипеда, построенного на
векторах
ar = 3i + j − k , b = −i + k , cr = 2i + 3 j .
27. Вычислить объём пирамиды, вершины которой находят ся в точках A(4, 3, 1), B(2, –1, 3), C(0, 1, 1), D(–3, 1, 4).
28. Новая система координат на плоскости получена из дан ной системы OXY переносом начала О в точку О1(1, –2) и пово ротом осей на угол 30°. Зная координаты точки М(4, 2) в новой системе, найти координаты её в старой системе.
11. Ответы к упражнениям
|
uuur |
|
1 |
|
r |
r |
|
uur |
r uuur |
r |
uuur |
r |
|||||
1. |
CM |
= |
|
( |
2a |
+ b ). 2. |
AB = |
8m, DA = −3 |
2n, CD = −2m , |
||||||||
|
3 |
||||||||||||||||
uur |
|
|
|
r |
|
r uuur |
= 3 |
r |
r uuur |
r |
r |
|
|||||
BC = 3 |
2n |
−6m , AC |
2n + 2m , BD = |
3 2n |
− 8m . |
|
|||||||||||
3. |
|
uuur |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
4. M (4 , 4 |
2 , 4). |
|
|
AB |
= 4 |
|
2 , cosα = |
|
, cos β = − |
. |
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. а) ПрOX a = 1, ПрOY ar = 6 , ПрOZ ar = −8 ; б) b = 7 (±2, ± 3, m 1) ;
в) ar20 = |
1 |
|
(1, 0, 2). |
6. Не коллинеарны. |
7. ar = −b + cr . |
||||||||||
5 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
r |
|
r |
r |
|
|
|
5 − 2 2 ; |
|||
8. a = 24,5 p + 21,5q |
+ 10r . 9. а) 13; б) –105. 10. а) 3 |
||||||||||||||
б) |
3 7 |
|
; |
в) |
9 |
21 |
. |
11. а) –6; б) –20; в) |
43 |
; г) |
3 |
14 |
. |
||
|
|
|
14 |
7 |
|
49 |
|||||||||
14 |
|
|
|
|
|
|
|
|
|
|
|||||
128
