
- •2. Линейные операции над векторами.
- •1) Сложение векторов.
- •2. Вычитание векторов.
- •3. Умножение векторов
- •Математически верная формулировка
- •Вопрос №16. Взаимное расположение прямых и плоскостей. Точка пересечения прямой и плоскости.
- •Первый замечательный п на прямой, то векторы редел
- •Теорема о замене функции на эквивалентную под знаком предела
Вопрос №1 Вектор . Линейные операции над веторами.
Операции:
Сложение а+б ( по правлу треугольника). Так же можно пременить правило параллелограмма , для этого нужно соединиь два вектора концами с помощью точки Y. Дальше до строить до параллелограмма. Сумма веторов а и б будет их одна из диоганалей.
Разность: а-б=ОА-ОБ=БА.
Умножение ветора на число. При условиях если К>0 тосонаправлен, если K<0 то противоположно направлен.
Вектор –это направленый отрезок прямой , те. Отрезок у которого одна из ограничевающих его точек принимает за начало , а другая за конец.
2. Линейные операции над векторами.
1) Сложение векторов.
Свойства сложения векторов.
Свойство комутативности (вектор а + в = в+а)
Свойства ассоциативности (ветора а+в) +с=а+(в+с)
Свойства существования вктора,нейтрального относительно операции сложения( а+0=0)
2. Вычитание векторов.
3. Умножение векторов
Свойства умножения векторов.
Свойства оссоциативности относительно числового множителя (альфа(бэтта *вектор А)= (альфа*бэтта)* ветор А).
Свойства дистрибутивности вкторного множителя относительно операции сложения чисел.
Свойства дистрибутивности числового множителя относительно операции сложения вектор.(альфа*(вектора А+В)= альфа*А+альфа *В.
«2» условие коллинеарности векторов (в координатах)
Если ветор а =(х.y,z) u b=(x2,y2,z2);
Имеет вид x1=mx2,y1=my2,z1=mz2 то получается ил x1/y1=x2/y2=z1/z2=M
Если m>0, то векторы а и в имеют одинаковый напрвления.
Если m<0, то векторы имеют противоположное направление.
Вопрос №3 Проекция ветора на ось.
Пусть в пространстве данны два вектора а и в . Отложим от произвольной точки О векторы ОА=а, ОВ=в. Углом между веторами а и в называется наименьший из углов ,угол АОВ ( при (веторах а ;b )= фи , при 0<=фи<=Пи.
Расмотрим ось L и отложим на нtй единичный отрезок вектор e(т.е что вектор ,длина которго равна единице). Под углом между векторами а и осью L понимают угол фи, между векторами a и e . Пусть L некоторая ось и вектор а = вектору AB. Обозначим через А1 и В1 проекции на ось L, соответственно точек А и В , предположим что А, имеет координату х1, а В1 координату х2 на оси L.
Тогда проекцией вектора AB на ось L , называется разность х1-х2 между координатами проекций конца и начала вектора AB на эту ось.
Проекция вектора а на ось L .
Из этого следует что видно , что угол между векторами а и осью L , если этот угол тупой то, х2-х1и проекция х2-х1=0 .
Если вектор а перпендикулярен оси l то х2=х1 и х2-х1 =0
Из этого следует что проекция ветора AB на ось L –это длина отрезка A1B1 взятая с определенным знаком и следовательно проекция вектора на ось это число или сколяр.
Вопрос №4
Базис в пространнстве- это тройка не компланарных векторов взятая в определенном порядке.
Ортонормированый базис- это когда , векторы этой системы папарно ортонормированы ( тоесть перпендикулярны) и имеют длину равную единице.
Ортонормированый базис (находится в дикартовой системе координат)
Ортонормированый базис – это когда их скалярное произведение равно нулю.
Кординаты вектора – это координаты точки.
В
 опрос
№6. Длина и направляющие косинусы
вектора.
опрос
№6. Длина и направляющие косинусы
вектора.Направляющие косинусы вектора
Направление вектора в пространстве определяется углами
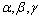 ,
которые вектор образует с осями координат
(рис. 12). Косинусы этих углов называютсянаправляющими косинусами вектора:
,
которые вектор образует с осями координат
(рис. 12). Косинусы этих углов называютсянаправляющими косинусами вектора:
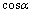 ,
,
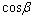 ,
,
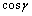 .
.Из свойств проекций:
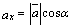 ,
,
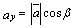 ,
,
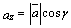 .
Следовательно,
.
Следовательно,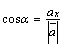 ,
,
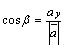 ,
,
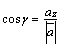 .
.Легко показать, что
1)
 ;
;2) координаты любого единичного вектора совпадают с его направляющими косинусами:
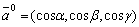 .
.Длина вектора равна расстоянию между точками Аи В:
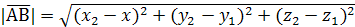
Зная координаты начала и координаты конца вектора, можно определить координаты самого вектора. Если точки заданы своими координатами
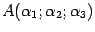 ,
,
 ,
то
,
то
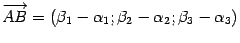
Вопрос №7
«1» Скалярное произведение – это число равное произведению длин этих векторов на косинус угла между ними.
Вектор а*b=|a|*|b|*cos (a,b);
«2» Свойства скалярного произведения.
Коллинеарность двух векторов
Векторы а и в
a*b =+-- |a|*|b|
+ когда вектор a|| b
когда а и в противо направлены.
Вопрос №8 векторы произведения
Векторы произведения двух векторов а и в – это треттььи вектор с.
Векторы а*в = Se, Se - площадь парраллелограмма.
e- орты направления а*в.
«2» Свойства .
Модуль вектора а равен произведению модулей вектора а и в на синус между ними.
Вектор перпендикулярен плоскости опеределяемой вектора а и в.
Вектор с направлен ,так, что из конца вектора с , происходящим против часовой стрелки.
Вопрос № 9
Сме́шанное произведе́ние![]() векторов
векторов![]() —
скалярное произведениевектораана
векторное произведение векторов
—
скалярное произведениевектораана
векторное произведение векторов![]() и
и![]() :
:
![]()
Смешанное произведение кососимметричнопо отношению ко всем своим аргументам:
![]()
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
![]()
Смешанное произведение
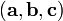 в
правой декартовой системе координат
(в ортонормированном базисе) равноопределителюматрицы,
составленной из векторов
в
правой декартовой системе координат
(в ортонормированном базисе) равноопределителюматрицы,
составленной из векторов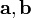 и
и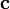 :
:
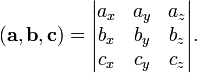
Смешанное произведение
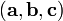 в
левой декартовой системе координат (в
ортонормированном базисе) равноопределителюматрицы,
составленной из векторов
в
левой декартовой системе координат (в
ортонормированном базисе) равноопределителюматрицы,
составленной из векторов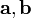 и
и ,
взятому со знаком "минус":
,
взятому со знаком "минус":
 р
р
В частности,
Если три вектора линейно зависимы(т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
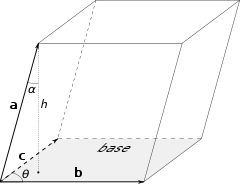
Геометрический смысл — Смешанное произведение
 по
абсолютному значению равно объёмупараллелепипеда(см. рисунок), образованного векторами
по
абсолютному значению равно объёмупараллелепипеда(см. рисунок), образованного векторами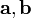 и
и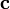 ;
знак зависит от того, является ли эта
тройка векторов правой или левой.
;
знак зависит от того, является ли эта
тройка векторов правой или левой.
![]()
Три вектора, определяющие параллелепипед.
Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
![]()
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).
Вопрос №10Общее уравнение прямой на плоскости.
Ах+By+C=0
Если А=0 ,то прямая параллельна оси Ох.
Если В=0 , то пряма парраллельна оси Оу.
С=0 , то прямая происходит через начало.
А,В- Координаты нормального вектора(n) и он перпендикулярен.
С- просто координатой.
Пример: 3x+5y+7=0
«2»
Растояние от точки М1(x1;y1); до прямойAx+By+C=0:
D=
Вопрос№11Каноническое уравнение прямой на плоскости.
Пусть Mo(x0;y0); - заданная точка прямой , аq=(m,n); - вектор , коллинеарный прямой( направляющий вектор прямой). Если М(х;y), - произвольная точка на прямой , то векторы,M0M=(x-x0;y-y0) и векторq=(m;n), коллинеарны , т.е координаты этих векторов пропорциональны.
Формула : x-x0/m=y-yo/n- каноническое уравнение.
«2»
x-x0/x1-x0 =y-y0/y1-y0.- уравнение прямой , проходящей через две точки.
Вопрос №12. Уравнение прямой с угловым коэффициентом.
Пусть дана прямая L на координатнойплоскостиОху.
Определение. Углом наклона прямой к оси абсцисс называется уголповорота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.
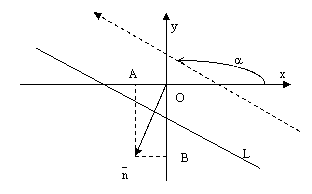
рис.1.
Из определенияследует, чтоуголнаклона
![]() прямой
L к оси Ох может изменяться от нуля до
прямой
L к оси Ох может изменяться от нуля до
![]() :
:
![]() .
Если прямая
.
Если прямая
![]() ,
то
,
то
![]() .
.
![]() Пусть (1)
Пусть (1)
– общее уравнение прямой L, где
![]() –
нормальный вектор прямой L и
–
нормальный вектор прямой L и
![]() .
Тогда
.
Тогда
![]() и
и
![]() (см.
рис.1). Выразим у изуравнения(1)
(см.
рис.1). Выразим у изуравнения(1)
![]() .
.
![]() ,
,
![]() .
.
Уравнение прямой L принимает вид:
![]() .
.
Определение. Уравнение прямой вида
![]() (2)
(2)
называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.
Теорема. В уравнении прямой с угловым коэффициентом
![]()
угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:
![]() .
(3)
.
(3)
Доказательство. 1) Если
прямая
![]() ,
то
,
то
![]() и
и
![]() .
С другой стороны, ее нормальный вектор
.
С другой стороны, ее нормальный вектор
![]() и
и
![]() .
.
Тогда
![]() и,
следовательно,
и,
следовательно,
![]() ,
ч.т.д.
,
ч.т.д.
2![]()
![]()
 )
Пусть
)
Пусть
![]() ,
тогда
,
тогда
![]() ,
,
![]() и
и
![]() .
Пусть F – точка пересечения прямой L сосьюабсцисс.
.
Пусть F – точка пересечения прямой L сосьюабсцисс.
Тогда
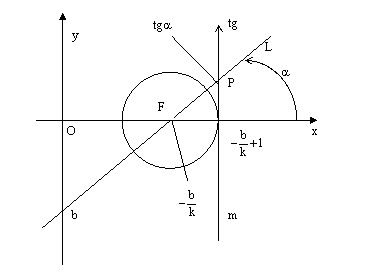
Опишем окружность единичного
радиуса с центром в точке F , а в точке
оси Ох с координатой
![]() проведем
касательную m к этой окружности. См.
рис.2.
проведем
касательную m к этой окружности. См.
рис.2.
рис.2.
Выберем положительное направление
на прямой m, так, чтобы
![]() .
Тогда ось m являетсяосьютангенсов для данной единичной
(тригонометрической) окружности.
.
Тогда ось m являетсяосьютангенсов для данной единичной
(тригонометрической) окружности.
Пусть Р – точка пересечения
прямой L с осьютангенсов m. Тогда, с одной стороны,
![]() ,
где
,
где
![]() –уголнаклона прямой L к оси Ох, а, с другой
стороны, точка
–уголнаклона прямой L к оси Ох, а, с другой
стороны, точка
![]() и
и
![]() ,
откуда и следуетравенство
,
откуда и следуетравенство
![]() ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
![]() –
уравнение прямой с угловым коэффициентом,
где
–
уравнение прямой с угловым коэффициентом,
где
![]() –
угловой коэффициент прямой, а
–
угловой коэффициент прямой, а
![]() –
отрезок, отсекаемый прямой на оси
–
отрезок, отсекаемый прямой на оси
![]()
Вопрос №13. Общее уравнение плоскости. Взаимное расположение плоскостей. Расстояние от точки до плоскости.
Общее уравнение плоскости:Ax+By+Cz+D= 0
где А, В, С – координаты вектора -вектор нормалик плоскости.
Взаимное расположение плоскостей:
Параллельные плоскости
Получим условия параллельности или
совпадения двух плоскостей
![]() и
и
![]() заданных
общими уравнениями:
заданных
общими уравнениями:
(![]() 4.23)
4.23)
Необходимым и достаточным условием
параллельности или совпадения плоскостей
(4.23) является условие коллинеарности
их нормалей
![]() Следовательно, если плоскости (4.23)
параллельны или совпадают, то
Следовательно, если плоскости (4.23)
параллельны или совпадают, то
![]() т.е.
существует такое число
т.е.
существует такое число
![]() что
что
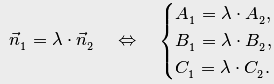
и наоборот.
Плоскости совпадают, если помимо этих
условий справедливо
![]() Тогда
первое уравнение в (4.23) имеет вид
Тогда
первое уравнение в (4.23) имеет вид
![]() т.е.
равносильно второму, поскольку
т.е.
равносильно второму, поскольку
![]()
Таким образом, плоскости (4.23) параллельны
тогда и только тогда, когда соответствующие
коэффициенты при неизвестных в их
уравнениях пропорциональны, т.е.
существует такое число
![]() что
что
![]()
![]()
![]() но
но
![]() Плоскости
(4.23) совпадают тогда и только тогда,
когда все соответствующие коэффициенты
в их уравнениях пропорциональны:
Плоскости
(4.23) совпадают тогда и только тогда,
когда все соответствующие коэффициенты
в их уравнениях пропорциональны:
![]()
![]()
![]() и
и
![]()
Условия параллельности и совпадения
плоскостей (4.23) можно записать в виде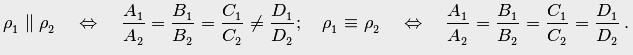
Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):
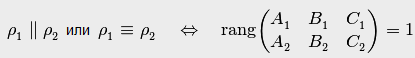
![]() или
или
Поверхности уровня линейного четырехчлена
П![]() оверхностью
уровняфункции
оверхностью
уровняфункции
![]() трех
переменных называется геометрическое
место точек координатного пространства
трех
переменных называется геометрическое
место точек координатного пространства
![]() в
которых функция принимает постоянное
значение, т.е.
в
которых функция принимает постоянное
значение, т.е.
![]()
Для линейного четырехчлена уравнение
поверхности уровня
![]() имеет
вид
имеет
вид
![]() (4.24)
(4.24)
При любом фиксированном значении
постоянной уравнение (4.24) описывает
плоскость. Рассмотрим поведение семейства
поверхностей уровня, отличающихся
значением постоянной. Поскольку
коэффициенты
![]() и
и
![]() не
изменяются, то у всех плоскостей (4.24)
будет одна и та же нормаль
не
изменяются, то у всех плоскостей (4.24)
будет одна и та же нормаль
![]() Следовательно,
поверхности уровня линейного четырехчлена
Следовательно,
поверхности уровня линейного четырехчлена
![]() D
представляют собой семейство параллельных
плоскостей (рис.4.19). Поскольку нормаль
совпадает с градиентом (см. пункт 3
замечаний 4.2), а градиент направлен в
сторону наискорейшего возрастания
функции, то при увеличении постоянной
поверхности уровня (4.24) переносятся
параллельно в направлении нормали.
D
представляют собой семейство параллельных
плоскостей (рис.4.19). Поскольку нормаль
совпадает с градиентом (см. пункт 3
замечаний 4.2), а градиент направлен в
сторону наискорейшего возрастания
функции, то при увеличении постоянной
поверхности уровня (4.24) переносятся
параллельно в направлении нормали.
Пересекающиеся плоскости
Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:
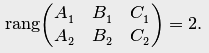
(4.25)
При этом условии система уравнений
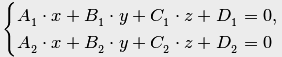 имеет
бесконечно много решений, которые
определяют прямую пересечения плоскостей,
заданных уравнениями (4.23).
имеет
бесконечно много решений, которые
определяют прямую пересечения плоскостей,
заданных уравнениями (4.23).
Расстояние от точки до
плоскости- это наименьшее из расстояний
между этой точкой и точками плоскости.
Известно, что расстояние от точки до
плоскости равно длине перпендикуляра,
опущенного из этой точки на плоскость.
Если плоскость задана уравнением
![]() ,
то расстояние
,
то расстояние
![]() от
точки
от
точки
![]() до
этой плоскости можно вычислить по
формуле
до
этой плоскости можно вычислить по
формуле![]() .
.
