3.Исследование релейной следящей системы методом фазового пространства.

Дальнейшее повышение крутизны нелинейной характеристики не приводит к качественным изменениям фазового портрета. При этом лишь возрастает частота затухающих колебаний. Качественный скачок наблюдается при предельном переходе 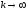. В этом случае нелинейная характеристика становится разрывной и соответствует характеристике идеального реле. Однако даже в этом случае потери устойчивости следящей системы не происходит, т.к. вещественная часть корней остается отрицательной. Фазовая плоскость состоит при этом из двух областей, соответствующих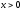и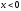(рис.20.4). Ввиду того, что линейная зона при этом исчезает, фазовый портрет состоит из траекторий, определяемых соотношением (20.4).

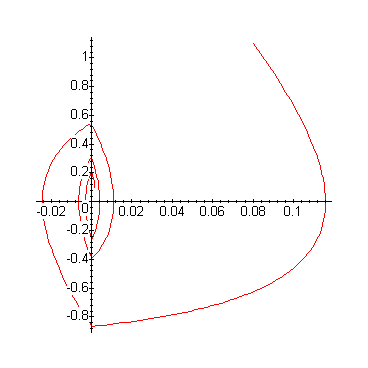
Рис.20.5.Фазовый портрет следящей системы с идеальным реле.

Затухание колебаний в релейной системе можно объяснить достаточно простыми рассуждениями, опираясь на свойства слагаемых, составляющих соотношение (20.4).

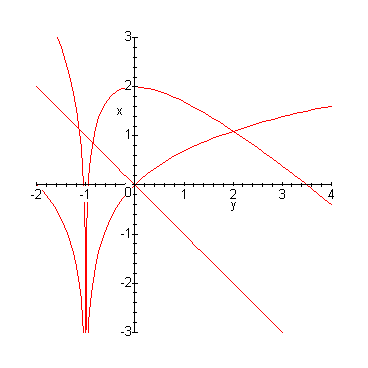
Рис.20.6. Фазовая траектория релейной

системы и ее составляющие

На рис.20.6 изображающая точка движется справа налево. При этом крутизна логарифмической составляющей монотонно возрастает, в то время как у линейной составляющей она остается постоянной. Поэтому длина отрезков, отсекаемых фазовой траекторией на оси y монотонно убывает.

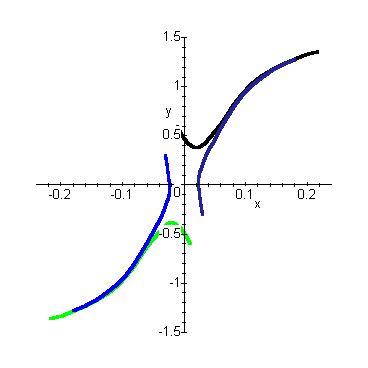При изменении знака обратной связи следящая система становится неустойчивой и начало координат становится точкой типа «седло». Фазовый портрет в этом случае имеет вид, изображенный на рис.20.7.

Рис.20.8.Фазовый портрет системы

с положительной обратной связью.

Начальные значения координат выбраны в малой окрестности особой точки. Спустя 0.3с изображающая точка оказывается далеко вне зоны линейности и при неограниченном времени уходит в бесконечность.

Ни при каких значениях параметров k и T в этой следящей системе не образуется точка типа «центр». Однако если заменить апериодический элемент на интегрирующий, то такая точка возникнет. Нетрудно видеть, что дифференциальное уравнение при малых отклонениях x имеет вид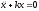. (20.5)

Корни характеристического уравнения равны 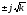, что и соответствует особой точке типа «центр». Уравнение вида (20.5)

Описывает также колебания математического маятника без рассеивания энергии.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6

1.Годограф частотного оператора системы автоматического управления.

Введем понятие годографа в комплексной плоскости, т.е. в системе координат по осям которой будем отсчитывать значения вещественной и мнимой частей функции 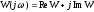. Таким образом, годограф является отображением мнимой оси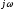на комплексную плоскость.

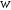2. Синтез следящей системы с заданными показателями качества.

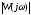Быстродействие следящей системы не является ее единственным показателем качества. Построенная частотная характеристика часто оказывается в противоречии с требованием точности воспроизведения плавных входных функций. Как мы видели, эта точность зависит от добротности системы. Графически это означает, что низкочастотная асимптота амплитудной характеристики должна проходить достаточно высоко, чему не отвечает, например, рисунок 11.3. Попытка найти компромиссное решение задачи реализации системы, обладающей заданными показателями по точности и по быстродействию, приводит к понятиюжелаемой логарифмической характеристики.

При конструировании автоматических систем обычно имеется заданный набор элементов, параметры которых трудно изменить. Например, для изменения параметров исполнительного двигателя приходится целиком пересмотреть его конструкцию. Совокупность таких элементов образует неизменяемую часть. Для получения желаемой характеристики к неизменяемой части подключаются элементы коррекции, характеристики которых меняются легко. Обычно такими элементами служат пассивные электрические четырехполюсники. На рис.11.4 показано последовательное включение неизменяемой части и корректирующей цепи. Передаточная функция разомкнутой цепи равна произведению передаточных функций последовательного соединения, а логарифмические характеристики при этом суммируются: 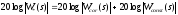,здесь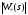- желаемая передаточная функция, а две другие не требуют пояснений.

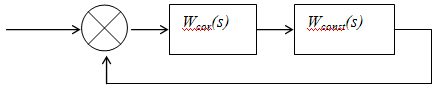
Рис.11.4.Последовательное включение элементов коррекции.

Можно также охватить часть схемы гибкой обратной связью, как показано на рис.11.5. При этом передаточная функция этой связи подбирается таким образом, чтобы вся схема приобрела характеристику либо равную, либо максимально близкую к желаемой.

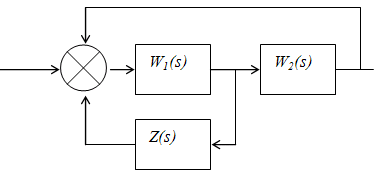
Рис.11.5.Параллельное включение корректирующих элементов.

В последнем случае следует очевидное соотношение 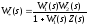,(11.5)

из которого и находится передаточная функция гибкой обратной связи Z(s). Вычисление становится особенно простым, если произведение в знаменателе существенно превосходит единицу. Тогда, переходя к логарифмическим характеристикам, можно записать приближенную формулу для определения передаточной функции корректирующего элемента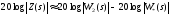. (11.6)

Обращаю ваше внимание на то, что мы всюду оперируем с амплитудными частотными характеристиками. Но в логарифмических координатах аналогичные соотношения справедливы и для фазовых частотных характеристик. Кроме того, по виду амплитудной характеристики для линейной системы с сосредоточенными параметрами всегда можно построить фазовую характеристику, ибо они связаны однозначно. Системы, обладающие таким свойством, называются минимально фазовыми.