2.Какое влияние оказывает элемент с запаздыванием на характеристики системы управления?

пусть передаточная функция разомкнутой системы имеет вид 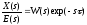, гдеW(s) - передаточная функция части системы, не имеющей запаздывания.

Заметим, что передаточные функции систем с сосредоточенными параметрами обладают свойством взаимно однозначного соответствия между амплитудной и фазовой частотными характеристиками. Такие системы называются минимально фазовыми. Системы с распределенными параметрами и, в частности, системы с запаздыванием не являются минимально фазовыми, ибо элемент с произвольным запаздыванием имеет амплитудную характеристику, тождественно равную единице. В то же время его фазовая характеристика представляет собой линейную функцию частоты.

Первая проблема, которую необходимо решить в случае наличия запаздывания, это анализ устойчивости. Записывая характеристическое уравнение замкнутой системы в виде 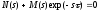,гдеN (s) и M (s) – полиномы, нетрудно заметить, что применение алгебраического критерия Гурвица в данном случае невозможно, ибо характеристическое уравнение имеет неограниченный порядок. В то же время использование любого частотного критерия не встречает препятствий. Рассмотрим, например, простейший случай последовательного включения интегрирующего и запаздывающего элементов. Построим годограф функции (рис.16.2) 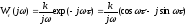. Минимальное значение частоты, при котором годограф пересекает вещественную ось, находится из выражения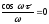, откуда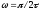. При этом вещественная часть частотного оператора равна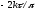и, следовательно, условием устойчивости будет неравенство.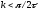

В данном случае неравенство определяет граничное значение коэффициента усиления. Из этого же условия нетрудно найти критическое значение запаздывания при заданном коэффициенте усиления.

Как видим, запаздывающий элемент в одноконтурной системе может вызвать неустойчивость. Совсем иное влияние может оказать запаздывание в местной обратной связи. В некоторых случаях оно может дать стабилизирующий эффект.

3.Качественный анализ переходных процессов в нелинейных системах, описываемых уравнениями высокого порядка.

Современные вычислительные средства существенно облегчают построение переходных процессов в нелинейных системах при отсутствии каких-либо допущений. Однако часто оказывается полезным предварительное исследование с использованием приемов гармонической линеаризации в несколько измененной форме. Для качественного исследования переходного процесса воспользуемся тем же представлением выхода, что и при анализе периодических режимов, но амплитуду a и угол  будем рассматривать как функции времени, т.е. 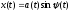(27.1)

В линейных системах эти функции имели вид .

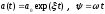Последние формулы можно рассматривать как решения простейших линейных уравнений 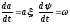.(27.2) В случае нелинейных систем параметры дзета иомега зависят от амплитуды, но при гармонической линеаризации мы будем использовать формулы (27.2). Таким образом, дифференцируя, имеем 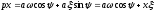(27.3) где использован обычный символ дифференцирования.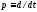

Далее, запишем уже известное выражение для линеаризованного нелинейного элемента 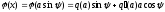. Или, используя (27.1) и (27.3)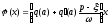,где коэффициенты линеаризации вычисляются по известным формулам (23.4).

Линеаризованное дифференциальное уравнение замкнутой системы будет иметь вид 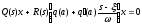.(27.4)

Заметим, что формулы (27.2) соответствуют переходному процессу вида 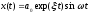,который имеет место при паре комплексно-сопряженных корней характеристического уравнения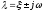. Подставив это значение в характеристическое уравнение, соответствующее (27.4), запишем соотношение между параметрами, определяющими форму переходного процесса.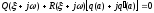

Выделяя вещественную и мнимую части из полученного равенства, получим два уравнения для вычисления указанных параметров 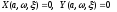.(27.5)

Решая их, например, при различных значениях a , получим зависимости параметров переходного процесса вида 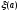и.

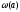Определенный интерес может представить решение системы (27.5) при 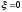. В этом случае в пространстве параметров можно построить границу, разделяющую это пространство на области, которым соответствуют переходные процессы, либо затухающие до нуля, либо стремящиеся к установившимся автоколебаниям. Приводимый пример поможет лучше усвоить методику такого разделения.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 18