
- •1.Методы математического описания линейных систем управления.
- •2.Связь между частотными критериями устойчивости и методами выделения области устойчивости в пространстве параметров.
- •3.Аналитическое описание нелинейных элементов. Кусочно-линейная аппроксимация.
- •1.Типовые тестовые воздействия и их краткая характеристика.
- •2.Импульсная переходная характеристика линейной системы управления.
- •3.Метод фазового пространства исследования нелинейных систем.
- •1.Периодические и непериодические сигналы. Преобразование Лапласа.
- •2.Коэффициенты ошибок следящих систем.
- •3.Типы особых точек фазового пространства.
- •1.Передаточная функция линейной динамической системы. Классификация элементов.
- •2.Каким порядком астатизма должна обладать следящая система, чтобы при входном воздействии вида tn установившаяся ошибка была равна нулю?
- •3.Исследование следящей системы с нелинейным элементом типа «линейная зона с участками насыщения».
- •1.Общий вид дифференциального уравнения многомерной системы управления.
- •2.Оптимальный переходный процесс. Возможности реализации.
- •3.Исследование релейной следящей системы методом фазового пространства.
- •1.Годограф частотного оператора системы автоматического управления.
- •2. Синтез следящей системы с заданными показателями качества.
- •3.Исследование релейной следящей системы с гистерезисом.
- •1.Построить логарифмические характеристики заданного элемента.
- •2.Последовательность операций при построении характеристик корректирующих устройств.
- •3.Использование простых итераций при анализе нелинейных систем. Условия сходимости итераций.
- •1.Написать передаточную функцию по заданному графику амплитудной частотной характеристики.
- •2.Интегральная квадратическая оценка качества переходного процесса.
- •1.Построить логарифмическую частотную характеристику замкнутой следящей системы по заданному графику разомкнутой.
- •2.Интегральная оценка переходного процесса с экспоненциальным сглаживанием.
- •3. Исследование релейного автопилота. Скользящий режим.
- •1.Преобразование многоконтурных структурных схем.
- •2.Алгоритм поиска минимума интегральной оценки в пространстве параметров.
- •3.Метод гармонической линеаризации. Вычисление коэффициентов.
- •1.Записать передаточную функцию при заданной структурной схеме.
- •2.Связь между качеством переходного процесса и распределением нулей и полюсов передаточной функции.
- •3.Гармоническая линеаризация идеального реле.
- •1.Определение устойчивости движения по а.М. Ляпунову.
- •2.Способы модуляции в дискретных системах управления.
- •3.Аналитическое исследование автоколебаний при гармонической линеаризации.
- •1.Теорема а.М. Ляпунова об устойчивости для систем, допускающих линеаризацию.
- •2.Рекуррентные соотношения в дискретных системах управления.
- •3.Частотный подход к анализу автоколебаний.
- •1.Практическое применение критерия устойчивости Гурвица (не ниже 4-го порядка)..
- •2.Модификация критерия Гурвица для дискретных систем.
- •1.Доказать критерий устойчивости а.В. Михайлова.
- •2.Управляемость динамических систем. Теорема Калмана об управляемости.
- •3.Вынужденные колебания в нелинейных системах. Условия существования.
- •1.Доказать критерий устойчивости Найквиста.
- •2.Наблюдаемость динамических систем. Теорема Калмана о наблюдаемости.
- •3.Вынужденные колебания в нелинейных системах. Пороговая амплитуда возбуждающего сигнала. Вибрационное сглаживание разрывных характеристик.
- •2.Какое влияние оказывает элемент с запаздыванием на характеристики системы управления?
- •3.Качественный анализ переходных процессов в нелинейных системах, описываемых уравнениями высокого порядка.
- •1.В чем состоит основной принцип выделения границ области устойчивости в пространстве параметров?
- •2.Изложить аналитический подход к исследованию многомерной системы управления. Распространение понятия свертки на многомерные системы.
- •3.Выделение зон затухания и возрастания амплитуды автоколебаний нелинейных систем до установившегося значения.
- •1.Выделение области устойчивости в пространстве двух параметров. Особые прямые. Правила штриховки границы.
- •2.Сформулировать условия устойчивости линейной системы управления с медленно меняющимися параметрами.
- •3.Знакоопределенные и знакопостоянные функции. Связь с устойчивостью нелинейных систем.
- •1.Теорема а.М. Ляпунова об устойчивости в общем случае (с использованием знакоопределенных функций).
- •2.Анализ устойчивости релейной следящей системы с помощью функций а.М. Ляпунова.
- •3.Анализ устойчивости автопилота с нелинейным исполнительным элементом. Абсолютная устойчивость.
- •1.Общие приемы исследования нелинейных систем произвольного порядка.
- •2.Теоремы а.М. Ляпунова об асимптотической устойчивости и о неустойчивости.
- •1.Примеры элементов с нелинейными характеристиками.
- •2.Псевдолинейная коррекция частотных характеристик.
- •3.Преобразоание уравнения высокого порядка, описывающего линейную систему управления к нормальной системе в форме Коши.
2.Сформулировать условия устойчивости линейной системы управления с медленно меняющимися параметрами.
Для дальнейшего исследования устойчивости нам понадобится лемма Гронуолла-Беллмана.
Пусть
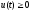 и
и при
при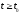 ,
,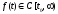 ,
причем при
,
причем при справедливо неравенство
справедливо неравенство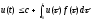 ,
гдеc
- положительная
постоянная. Тогда
,
гдеc
- положительная
постоянная. Тогда
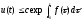 .
.
Пользуясь леммой, рассмотрим устойчивость линейной дифференциальной системы с почти постоянной матрицей.
Теорема.
Пусть система
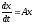 ,
(17.10) гдеA
– постоянная матрица, устойчива в смысле
Ляпунова. Тогда система
,
(17.10) гдеA
– постоянная матрица, устойчива в смысле
Ляпунова. Тогда система
 ,(17.11)
где
,(17.11)
где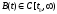 и
и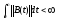 также устойчива.
также устойчива.
Доказательство.
Пусть
X
(t)
- фундаментальная матрица решений
системы (17.10) и X(0)=E
. Рассматривая
B
(t)
y
как возмущение
в (17.11) и пользуясь выводом (17.12) метода
вариации постоянных, запишем
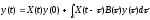 .
.
Т.к.
система (17.10) устойчива, то ее фундаментальная
матрица решений ограничена, т.е.
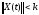 .
.
Следует
оценка сверху
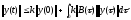 .
.
Теперь используем лемму Гронуолла-Беллмана, согласно которой
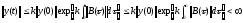 .
.
Таким образом, система (17.11) также устойчива, что и требовалось.
В
качестве простого примера рассмотрим
уравнение вида
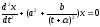 .
(17.12)
.
(17.12)
Вводя
обозначение
 ,
приведем его к нормальной форме Коши.
Очевидно, что в данном случае постоянная
матрица
,
приведем его к нормальной форме Коши.
Очевидно, что в данном случае постоянная
матрица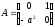 .
.
Сравнение
с (17.11) позволяет записать также
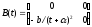 .
.
Принимая
в качестве нормы наибольшую абсолютную
величину элементов, имеем
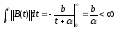 .
.
Согласно теореме, предшествующей примеру, решение должно оставаться ограниченным.
3.Знакоопределенные и знакопостоянные функции. Связь с устойчивостью нелинейных систем.
Рассмотрим
функцию
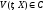 на некотором множестве
на некотором множестве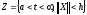 .
.
Здесь
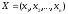 -n-мерный
вектор. Действительная непрерывная
функция
-n-мерный
вектор. Действительная непрерывная
функция
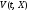 называетсязнакопостоянной
(знакоположительной
или знакоотрицательной),
если
называетсязнакопостоянной
(знакоположительной
или знакоотрицательной),
если
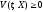 (или
(или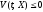 )
при
)
при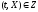 .
.
Далее,
функция
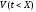 называетсяположительно
определенной,в
Z,
если существует скалярная функция
называетсяположительно
определенной,в
Z,
если существует скалярная функция
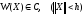 ,
такая, что
,
такая, что
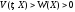 при
при
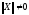 ,
,
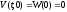 .
.
Пример 28.1.
Функция
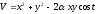 при
при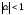 является положительно определенной,
т.к.
является положительно определенной,
т.к.
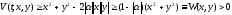
при x2 + y2 > 0; V =W= 0 при x = y = 0 .
При
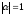 функцияV
всего лишь знакоположительна.
функцияV
всего лишь знакоположительна.
Аналогично
функция V
( t,
X
) называется
отрицательно определенной в Z
, если найдется
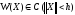 такая, что
такая, что
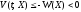 при
при
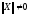
и
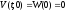 .
.
Положительно или отрицательно определенная функция называется знакоопределенной.
В
теории автоматического управления
функции, обладающие свойством положительной
(или отрицательной) определенности
введены А.М. Ляпуновым и играют основную
роль при анализе устойчивости. Они могут
принадлежать к различным классам. Нас,
в частности, будут интересовать
квадратичные
формы, т.е.
скалярные произведения вида
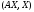 ,
гдеA=AT
– симметрическая матрица порядка
,
гдеA=AT
– симметрическая матрица порядка
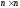 ,
аX=(x1,
x2
,…, x
n
)T
– вектор-столбец того же порядка. Таким
образом, скалярная квадратичная форма
записывается в виде
,
аX=(x1,
x2
,…, x
n
)T
– вектор-столбец того же порядка. Таким
образом, скалярная квадратичная форма
записывается в виде
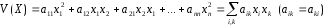 .(28.1)
.(28.1)
Матрица A называется матрицей квадратичной формы. Очевидно, матрица и функция (28.1) связаны взимнооднозначно.
Для выяснения свойства положительной определенности функции (28.1) служит критерий Сильвестра:
Для того, чтобы квадратичная форма V(X) была положительно определенной, необходимо и достаточно, чтобы определитель матрицы A и все ее диагональные миноры были положительны.
Пример 28.2.
Форма

не является положительно определенной. В самом деле, определитель
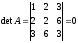 .
.
Заметим, что нулю равен и диагональный минор второго порядка.
Нетрудно
убедиться, что форма
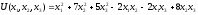 положительно определенная.
положительно определенная.
Вернемся теперь к понятию устойчивости движения, с которым мы познакомились в прошлом семестре (см. лекцию 7) и введем некоторые дополнительные определения.
Пусть
снова
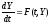 ,(28.2)
,(28.2)
где
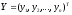 -
вектор состояния системы. При фиксированных
компонентах вектор состояния, как мы
знаем, указывает точку фазового
пространства. Невозмущенным движением
называется ограниченный вектор
-
вектор состояния системы. При фиксированных
компонентах вектор состояния, как мы
знаем, указывает точку фазового
пространства. Невозмущенным движением
называется ограниченный вектор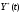 ,
удовлетворяющий уравнению (28.2), т.е.
,
удовлетворяющий уравнению (28.2), т.е.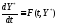 .(28.3)
.(28.3)
Разность
 называетсявозмущением.
Вычитая (28.3) из (28.2), получаем дифференциальное
уравнение в терминах возмущения
называетсявозмущением.
Вычитая (28.3) из (28.2), получаем дифференциальное
уравнение в терминах возмущения
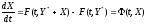 , (28.4)
, (28.4)
которое,
очевидно, обладает тривиальным решением
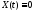 .В
пространстве
.В
пространстве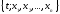 это тривиальное решение представляется
осью времени (рис.28.1).
это тривиальное решение представляется
осью времени (рис.28.1).
По-прежнему
будем называть тривиальное решение
устойчивым,
если для любого
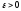 существует пара величин
существует пара величин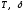 ,
таких, что из условия
,
таких, что из условия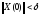 следует
следует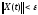 для любогоt
> T
.
для любогоt
> T
.
Если
величина
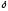 может принимать любое значение, то
система (и невозмущенное движение)
называетсяустойчивым
в целом.
может принимать любое значение, то
система (и невозмущенное движение)
называетсяустойчивым
в целом.
Наконец, если

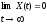
движение называется асимптотически устойчивым.
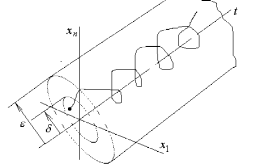
Рис.28.1. Геометрическая интерпретация
устойчивого тривиального решения.
Запишем теперь (28.4) в скалярной форме, т.е. в виде системы дифференциальных уравнений
 , (28.5)
, (28.5)
а
также продифференцируем по времени
функцию
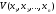 ,
имея в виду (28.5),
,
имея в виду (28.5),
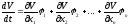 . (28.6)
. (28.6)
Выражение
(28.6) называется производной
функции V
в силу системы (28.5).
Компоненты
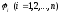 можно рассматривать как составляющие
вектора фазовой скорости. С другой
стороны, градиентом функцииV
называется вектор
можно рассматривать как составляющие
вектора фазовой скорости. С другой
стороны, градиентом функцииV
называется вектор
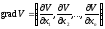 .
.
Выражение
(28.6) можно рассматривать как скалярное
произведение вектора градиента функции
V
на вектор фазовой скорости
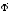 ,
т. е.(рис.28.2)
,
т. е.(рис.28.2)
 . (28.7)
. (28.7)
Производная
функции V
в силу системы (28.5) также является
функцией координат вектора состояния.
В дальнейшем введем для нее обозначение
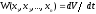 .
.
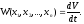
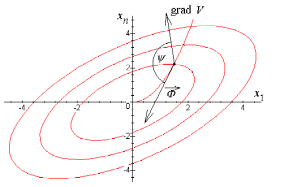
Рис. 28.2. Геометрическая интерпретация знака
производной в силу системы уравнений (28.5).
На рис.28.2 показано несколько линий уровня положительно определенной функции V. В малой окрестности начала координат они близки к эллипсам (это становится ясным, если вспомнить формулу разложения в ряд Тейлора функции многих переменных).
С другой стороны из (28.7) видно, что знак производной зависит от угла . В случае, когда угол острый, производная положительна, в случае тупого угла – она отрицательна. На рис.28.2 показан именно последний случай. При этом вектор фазовой скорости направлен вдоль фазовой траектории к началу координат, т.е. величина возмущения стремится к нулю. Это означает, что движение, описываемое уравнениями (28.5), устойчиво.
Подведем итог всему сказанному в виде теоремы Ляпунова об устойчивости.
Теорема.
Если для системы уравнений (28.5) существует знакоопределенная функция V ( X ), производная которой W ( X ) в силу системы (28.5) имеет противоположный знак по отношению к V, то решение системы устойчиво.
Доказательство.
Без
ограничения общности будем считать
функцию V
( X
) положительно
определенной. Выберем
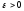 и положим
и положим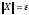 .
Обозначим
.
Обозначим
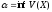
на
множестве
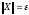 .
.
Поскольку
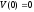 ,
то из непрерывности функцииV(X)
следует существование такого числа
>
0, что
,
то из непрерывности функцииV(X)
следует существование такого числа
>
0, что
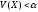 при
при
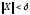 .
.
Положим
теперь, что начальные условия таковы,
что
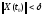 .
Из условия теоремы производная функцииV
отрицательна вдоль решения
.
Из условия теоремы производная функцииV
отрицательна вдоль решения
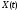 .
Поэтому функцияV
не может возрастать вдоль этого решения.
Следовательно,
.
Поэтому функцияV
не может возрастать вдоль этого решения.
Следовательно,
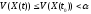 . (28.8)
. (28.8)
При
этом
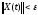 .
Если предположить, что это не так, то
есть найдется
.
Если предположить, что это не так, то
есть найдется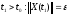 ,
тогда
,
тогда
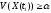 ,
,
что
противоречит (28.8). Остается утверждение
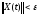 ,
что и требовалось.
,
что и требовалось.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 20
