1.Теорема а.М. Ляпунова об устойчивости в общем случае (с использованием знакоопределенных функций).
Если для системы уравнений (28.5) существует знакоопределенная функция V ( X ), производная которой W ( X ) в силу системы (28.5) имеет противоположный знак по отношению к V, то решение системы устойчиво.
Доказательство.
Без
ограничения общности будем считать
функцию V
( X
) положительно
определенной. Выберем
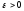и положим
.
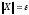Обозначим
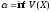
на
множестве
.
Поскольку
,
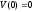то из непрерывности функцииV(X)
следует существование такого числа
>
0, что
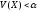при
.
Положим
теперь, что начальные условия таковы,
что
.
Из условия теоремы производная функцииV
отрицательна вдоль решения
.
Поэтому функцияV
не может возрастать вдоль этого решения.
Следовательно,
. (28.8)
При
этом
.
Если предположить, что это не так, то
есть найдется
,
тогда
,
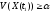что
противоречит (28.8). Остается утверждение
,
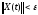что и требовалось.
2.Анализ устойчивости релейной следящей системы с помощью функций а.М. Ляпунова.
Рассмотрим элементарную релейную следящую систему, структурная схема которой изображена на рис.20.1. Ранее мы видели, что она обладает устойчивым положением равновесия (лекция 20). Покажем, что это так с помощью доказанной теоремы Ляпунова об устойчивости. Дифференциальное уравнение релейной следящей системы имеет вид
.
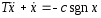Приведя его к нормальной форме Коши, получаем
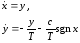(29.1)
Выберем функцию Ляпунова в виде
. (29.2)
Найдем производную функции Ляпунова в силу системы (29.1).
.
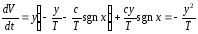Ввиду очевидной отрицательности производной приходим к выводу об устойчивости системы с идеальным реле.
В этом простом примере нам удалось подобрать функцию Ляпунова в виде (29.2), который типичен для следящих систем. Обратим внимание на то, что с точностью до постоянных множителей слагаемые функции Ляпунова представляют собой кинетическую и потенциальную энергию системы, а вся функция, таким образом, эквивалентна полной энергии. Физически сигнал на выходе релейного элемента эквивалентен силе, возвращающей следящую систему в положение равновесия X= (x, y)T =0. Работа, совершаемая возвращающей силой
.
Что касается кинетической энергии, то ее представляет квадрат фазовой скорости y . Этот принцип выбора функции Ляпунова во многих случаях помогает решить задачу об устойчивости нелинейной системы управления.
3.Анализ устойчивости автопилота с нелинейным исполнительным элементом. Абсолютная устойчивость.
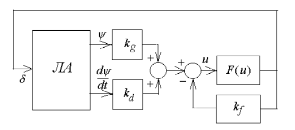
Рис.29.1.Автопилот с демпфирующим гироскопом.
Запишем уравнения элементов автопилота и управляемого летательного аппарата (ЛА).
. (29.3)
Здесь I–момент инерции летательного аппарата относительно оси, нормальной к плоскости управления и проходящей через центр масс, - коэффициент вязкого демпфирования в воздушной среде, k - коэффициент эффективности аэродинамического руля, - угол рыскания, - угол отклонения руля.
Рулевая машина с нелинейной характеристикой описывается уравнением
, (29.4)
где сигнал на входе рулевой машины
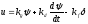. (29.5)
Здесь
-
коэффициент преобразования свободного
(с тремя степенями свободы) гироскопа,
-
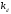коэффициент преобразования демпфирующего
гироскопа (с двумя степенями свободы),kf
-
коэффициент обратной связи силового
цилиндра.
Для дальнейших исследований полезно привести систему уравнений к наиболее простой форме Коши с минимальным количеством обобщенных параметров. Как мы видели на примере исследования скользящего режима (лекция 22), это достигается введением безразмерного времени и масштабных коэффициентов.
Введем обозначение (29.3)
,
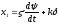и дифференцируя по времени, имеем
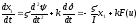. (29.6)
Сделаем
также замену
.
Тогда производная
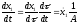
и вместо (29.6) можно записать
или,
полагая
,
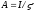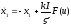.(29.7)
Нетрудно
заметить, что переменная
не измеряется в секундах и ее можно
рассматривать как «безразмерное время».
Обратимся теперь к уравнению (29.4) рулевой машины, которое также перепишем в виде
.
Умножив
обе части на
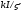и вводя обозначение
,
получим вместо (29.4)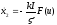
.(29.8)
Наконец,
дифференцируя (29.5), находим
.
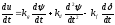Здесь
.
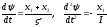Следовательно,
.
Для
перехода к безразмерному времени обе
части последнего соотношения следует
умножить на
.
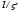В результате получим
.
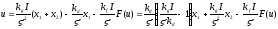Последнее
соотношение упростим за счет масштабного
коэффициента, введя третью компоненту
вектора состояния системы управления,
.
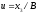Тогда, умножив обе части наB
и подобрав
значение
,
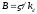а также используя обобщенный параметр
,
запишем третье уравнение системы управления
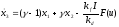.(29.9)
В выражениях (29.7),(29.8) и (29.9) нелинейная характери-стика осталась в старых обозначениях. Система уравнений приобретет наиболее простую форму, если обозначить
.
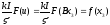При
этом
и система уравнений автопилота приобретет
вид
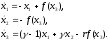(29.10)
Здесь
коэффициент
.
Обобщенные коэффициенты в системе уравнений (29.10) имеют следующий смысл: коэффициент выражает отношение сигнала по углу рыскания к сигналу по его производной, а коэффициент r характеризует величину отрицательной обратной связи, охватывающей силовой цилиндр рулевой машины.
Перейдем
к выбору функции Ляпунова. В случае
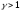(сигнал
по углу рыскания преобладает над сигналом
по производной) функцию Ляпунова выберем
в виде
(29.11)
Вычислим производную (29.11) по в силу уравнений (29.10).
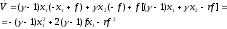(29.12)
Для того, чтобы обнаружить условие отрицательности производной (условие устойчивости) достаточно дополнить два первых слагаемых до полного квадрата, т.е.
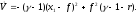
При
,
очевидно, производная будет отрицательна
при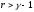
.
Тот же результат получается, если воспользоваться критерием Сильвестра. Изменив все знаки в правой части (29.12) на противоположные, найдем условие положительности выражения:
,
откуда следует уже полученное условие устойчивости.
Пусть
теперь сигнал по производной угла
рыскания будет настолько велик, что
обобщенный параметр
.
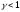Выясним условие устойчивости системы
управления в этом случае. На этот раз
выберем функцию Ляпунова, изменив знак
первого слагаемого по сравнению с
(29.11), т.е.
.
Дифференцируя по и учитывая (29.10), имеем
.
Раскрыв скобки, получаем совсем простое выражение
,
из
которого видно, что на этот раз устойчивость
автопилота обеспечивается положительностью
обратной связи силового цилиндра, т.е.
.
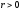Последнее условие ослаблено по сравнению
с предыдущим случаем. Сказывается
стабилизирующее влияние сигнала с
демпфирующего гироскопа.
В рассмотренном примере следует обратить внимание на то, что при анализе устойчивости конкретная форма нелинейной характеристики не играла роли. При выборе функции Ляпунова достаточно было предположить, что
,
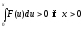а
также нечетность нелинейной характеристики,
т.е.
.
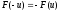Такими свойствами обладает достаточно
широкий класс нелинейных характеристик.
Например, такая характеристика показана
на рис. 29.2.
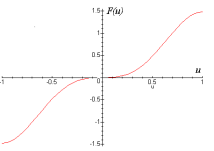
Рис.29.2. Нелинейная характеристика рулевой машины.
Свойство сохранения устойчивости независимо от вида нелинейной характеристики называется абсолютной устойчивостью нелинейной системы.
При
кусочно-линейной аппроксимации
характеристики рулевой машины в данном
случае обнаруживаются границы зоны
нечувствительности. Технически это
объясняется постепенным открытием щели
регулирующего клапана. Однако существуют
устройства типа «сопло-заслонка», у
которых такой зоны не существует. В
частности, можно представить в качестве
нелинейной характеристики функцию,
допускающую линеаризацию при малых
отклонениях, т.е.
.
Тогда вместо системы (29.10) будем иметь
линейную систему уравнений
Соответствующее характеристическое уравнение имеет вид
.
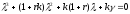Составив
определитель Гурвица, без труда обнаружим,
что условием устойчивости является
неравенство
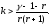
Интересно отметить, что это условие ограничивает коэффициент усиления снизу. Сравнив с условиями абсолютной устойчивости, убеждаемся, что коэффициент k при их выполнении может принимать любое положительное значение!
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 21